Onlinebrückenkurs Mathematik Abschnitt 1.2.1 Eingangstest für den Onlinekurs

Dies ist ein einreichbarer Test:

Im Gegensatz zu den offenen Aufgaben werden beim Eingeben keine Hinweise zur Formulierung der mathematischen Ausdrücke gegeben.
Der Test kann jederzeit neu gestartet oder verlassen werden.
Der Test kann durch die Buttons am Ende der Seite beendet und abgeschickt, oder zurückgesetzt werden.
Der Test kann mehrfach probiert werden. Für die Statistik zählt die zuletzt abgeschickte Version.

Aufgabe 1.2.2

Vereinfachen Sie diese Mehrfachbrüche so weit wie möglich:

$1 - \frac{1}{2} + \frac{1}{3} - \frac{1}{4}$ ist vereinfacht das Gleiche wie .
$\frac{x - \frac{1}{x}}{1 - \frac{1}{x}}$ ist vereinfacht das Gleiche wie .

Aufgabe 1.2.3

Multiplizieren Sie diesen Term vollständig aus und fassen Sie zusammen:

(a - b) (2 c + d)

=

Aufgabe 1.2.4

Wenden Sie jeweils eine binomische Formel an, um den Term umzuformen, so dass keine Klammerungen oder Wurzeln mehr auftreten:

$(2 \sqrt{3} + x \sqrt{3})^{2}$ = .
$(3 a - 4 b)^{2}$ = .

Aufgabe 1.2.5

Schreiben Sie diese Potenz- und Wurzelausdrücke als einfache Potenz mit einem rationalen Exponenten ohne das Wurzelzeichen zu verwenden:

$\sqrt{a b} \cdot \frac{1}{a} \cdot \sqrt{b^{3}}$ = .
$\sqrt{\sqrt{\sqrt{a} \cdot b} \cdot \frac{1}{c}}$ = .

Aufgabe 1.2.6

Formen Sie die Brüche so um, dass der Nenner verschwindet. In der Lösung dürfen keine Brüche und keine Potenzzeichen auftreten:

$\frac{12}{\sqrt{3}}$ = .
$\frac{1 + x - \sqrt{4 x}}{\sqrt{x} - 1}$ = .
$\frac{u^{3}}{\sqrt{u^{2} + 1} + 1}$ = .

Schreiben Sie hier ggf.

u^{3}

als u*u*u um die Verwendung von Potenzen zu vermeiden. Wurzeln

\sqrt{x}

können als sqrt(x) geschrieben werden.

Aufgabe 1.2.7

Die einzige Lösung der Gleichung

\frac{x - 2}{| x + 1 |} = \frac{1}{2}

ist

x

=
.

Aufgabe 1.2.8

Geben Sie die Lösungsmengen dieser Gleichungen an:

$\frac{1}{x} + 2 x = 2 - x$ hat die Lösungsmenge .
$x^{2} - 1 = (x - 1)^{3}$ hat die Lösungsmenge .
$\sqrt[7]{r} = r^{5}$ hat die Lösungsmenge .

Aufgabe 1.2.9

Bestimmen Sie sämtliche Lösungen der Betragsgleichung

| 5 x - 1 | = x^{2} - 1

.
Antwort: Die Lösungsmenge ist

L

=

.

Benutzen Sie keinen Taschenrechner! Wurzel- und Bruchterme dürfen in der Lösung auftreten.

Aufgabe 1.2.10

Geben Sie die Lösungsmenge der Ungleichung

x^{2} + 6 < - 5 x

in Intervallschreibweise an.
Antwort: Das Lösungsintervall ist
.

Aufgabe 1.2.11

Geben Sie die Lösungsmengen dieser Ungleichungen als Intervalle an, achten Sie dabei auf die Randpunkte:

$(x - 1)^{2} < x$ hat die Lösungsmenge .
$\sqrt{x^{2} - 1} < x$ hat die Lösungsmenge .

Aufgabe 1.2.12

Bestimmen Sie die Lösungsmenge für folgendes Lineares Gleichungssystem:

\begin{matrix} - x + 2 y & = & - 5 \\ 3 x + y & = & 1 \end{matrix}

Die Lösungsmenge

	ist leer,
	enthält genau eine Lösung: $x =$ , $y =$ ,
	enthält unendlich viele Lösungspaare $(x, y)$ .

Aufgabe 1.2.13

Geben Sie diejenige zweistellige Zahl an, die bei Vertauschen von Einer- und Zehnerziffer auf eine um 18 kleinere Zahl führt und deren Quersumme 6 ist.
Antwort:

Aufgabe 1.2.14

Für welchen Wert des reellen Parameters

α

besitzt das Lineare Gleichungssystem

\begin{matrix} 2 x + y & = & 3 \\ 4 x + 2 y & = & α \end{matrix}

unendlich viele Lösungen?
Antwort:

α =

Aufgabe 1.2.15

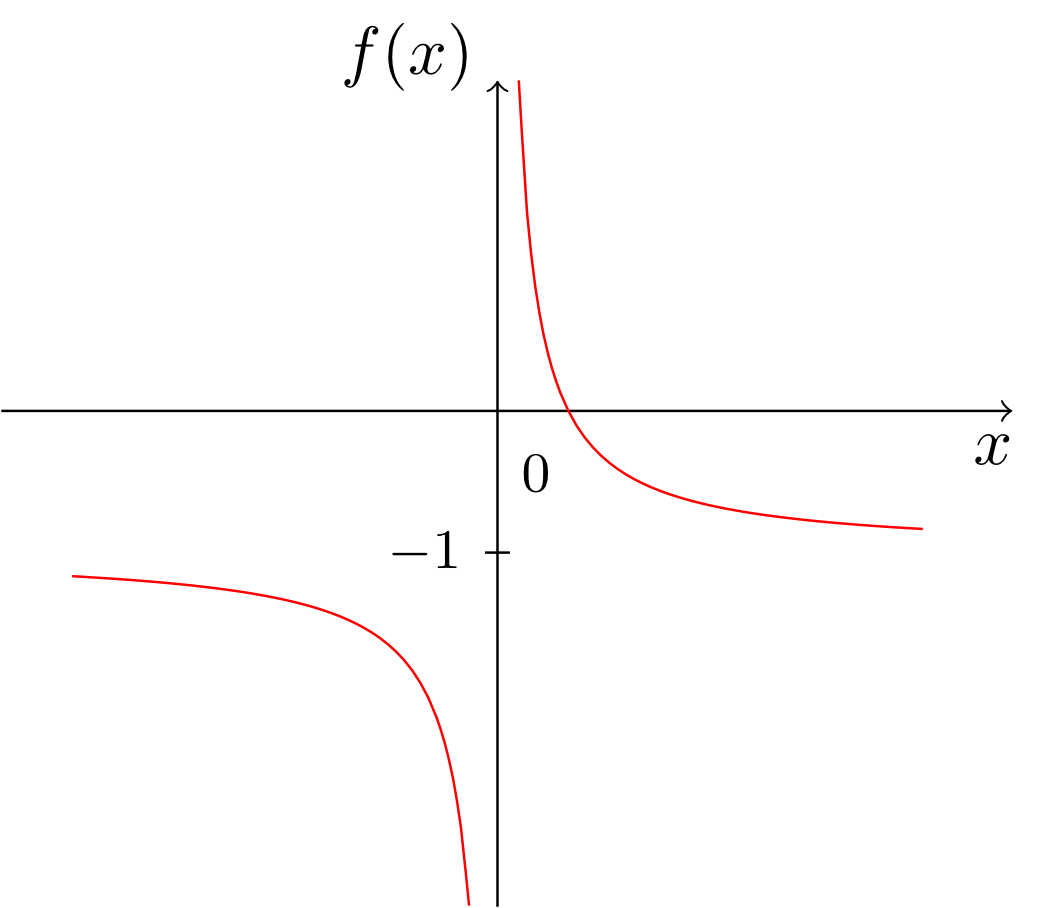
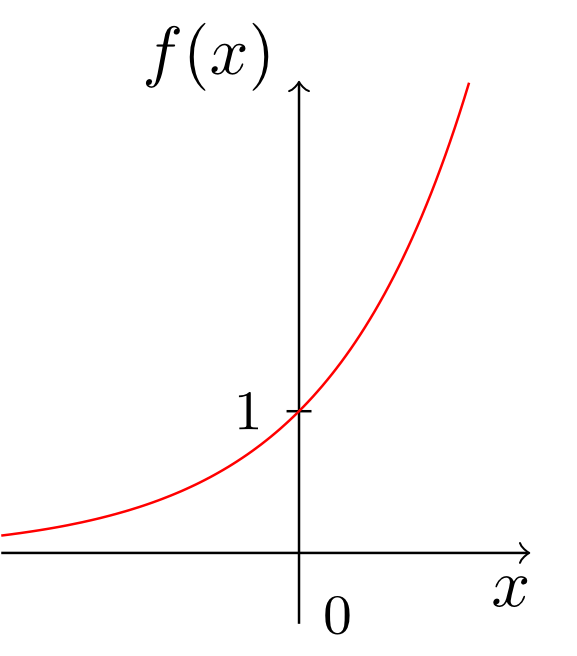
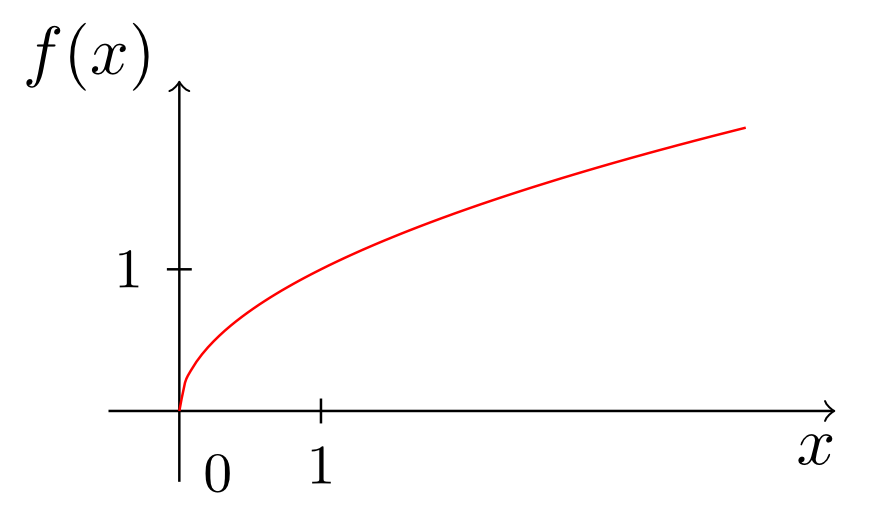
Ordnen Sie den folgenden Graphen die richtigen Abbildungsvorschriften der zugehörigen Funktionen zu:

Graph a) gehört zur Funktion $f (x)$ $=$ .
Graph b) gehört zur Funktion $f (x)$ $=$ .
Graph c) gehört zur Funktion $f (x)$ $=$ .
Graph d) gehört zur Funktion $f (x)$ $=$ .
Graph e) gehört zur Funktion $f (x)$ $=$ .

Wählen Sie dazu aus den folgenden Funktionsvorschriften und Eingabetermen aus (nicht alle kommen vor):

$f (x) = \sqrt{x}$	`sqrt(x)`
$f (x) = \frac{1}{2} x - 1$	`(1/2)*x-1`
$f (x) = \ln (1 - x)$	`ln(1-x)`
$f (x) = \ln (x)$	`ln(x)`
$f (x) = x^{1,5}$	`x^(1,5)`
$f (x) = \exp (x) = e^{x}$	`exp(x)`
$f (x) = (0,5)^{x}$	`(0,5)^x`
$f (x) = \frac{1}{x}$	`1/x`
$f (x) = \frac{1}{2 x} - 1$	`1/(2*x)-1`
$f (x) = \frac{1}{2} - x$	`1/x-x`

Sie können Eingabeterme markieren und in die Antwortfelder ziehen.
Geben Sie die Asymptote der Funktion mit der Abbildungsvorschrift a) an:
Es ist

lim_{x \to \infty} f (x)

=

Aufgabe 1.2.16

Die Abbildung zeigt zwei Geraden im 2-dimensionalen Raum.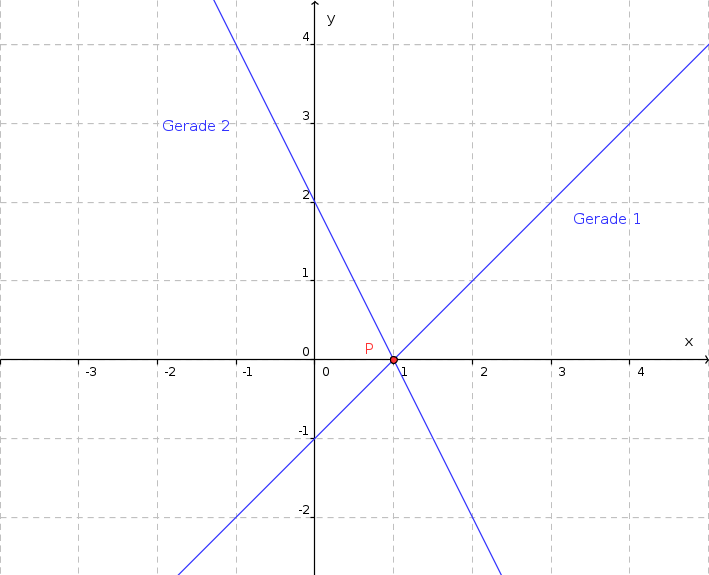

Stellen Sie die beiden Geradengleichungen auf:
Gerade 1:

y =

Gerade 2:

y =

Wieviele Lösungen besitzt das zugehörige Lineare Gleichungssystem?
Es besitzt

	keine Lösung,
	genau eine Lösung oder
	unendlich viele Lösungen.

Aufgabe 1.2.17

Geben Sie die Lösungsmenge für folgendes Lineare Gleichungssystem, bestehend aus drei Gleichungen mit drei Unbekannten, an:

\begin{matrix} x + 2 z & = & 3 \\ - x + y + z & = & 1 \\ 2 y + 3 z & = & 5 \end{matrix}

Die Lösungsmenge

	ist leer,
	enthält genau eine Lösung: $x =$ , $y =$ , $z =$ ,
	enthält unendlich viele Lösungen $(x, y, z)$ .

Aufgabe 1.2.18

Ein Lieferwagen, dessen Kilometerzähler

20

km anzeigt, startet seine Tour um sechs Uhr. Er erreicht sein Ziel vier Stunden später. Der Kilometerzähler zeigt jetzt

280

km. Berechnen Sie die mittlere Geschwindigkeit

v

, also die mittlere Änderungsrate zwischen Start- und Zielort. Setzten Sie dazu die fehlenden Zahlen und mathematischen Symbole

+

-

\cdot

/

in die folgende Rechnung ein:

v = (280

)

(

- 6) =

Aufgabe 1.2.19

Gegeben ist die Funktion

f : [- 3; 4] \to ℝ

, deren Graph hier gezeichnet ist.

In $x_{1} = 4$ ist die Ableitung gleich $0$ , nicht definiert, unendlich.
In $x_{2} = 0$ ist die Ableitung positiv, gleich $0$ , negativ.

Aufgabe 1.2.20

Berechnen Sie die erste und zweite Ableitung der Funktion

f : ℝ \to ℝ, x \to \frac{5 x}{3 + x^{2}}

, und geben Sie Ihr Resultat gekürzt und zusammengefasst an:

Erste Ableitung $f' (x) =$
Zweite Ableitung $f'' (x) =$

Klammern Sie die Terme um Missverständnisse zu vermeiden, z.B. schreiben Sie

\frac{x + 1}{(x + 2)^{2}}

als (x+1)/((x+2)^2).

Aufgabe 1.2.21

In welchen Bereichen ist die Funktion

f

mit

f (x) : = \frac{\ln x}{x}

für

x > 0

monoton fallend beziehungsweise monoton wachsend? Geben Sie Ihre Antwort in Form möglichst großer offener Intervalle

(r, s)

an:

$f$ ist auf
monoton wachsend.
$f$ ist auf
monoton fallend.

Offene Intervalle können in der Form

(a, b)

oder

(a; b)

eingetippt werden, geschlossene Intervalle als

[a, b]

oder

[a; b]

a

und

b

dürfen beliebige Ausdrücke sein. Verwenden Sie bei der Intervalleingabe nicht die Notation

] a, b [

für offene Intervalle.
Welche der Stellen

x_{1} = 1

x_{2} = 2

oder

x_{3} = 6

gehören zu einem Bereich, in dem

f

konvex ist?
Antwort:

Aufgabe 1.2.22

Bestimmen Sie jeweils eine Stammfunktion:

$\int (5 x^{4} + 8 x) d x =$
$\int 6 \sin (2 x) d x =$

Schreiben Sie Malpunkte (geschrieben als *) aus und setzen Sie Klammern um Argumente für Funktionen. Beispiele: Polynom: 3*x + 0.1, Sinusfunktion: sin(x), Verkettung von cos und Wurzel: cos(sqrt(3*x)).

Aufgabe 1.2.23

Berechnen Sie die Integrale:

\int_{- \frac{π}{2}}^{\frac{π}{2}} (x^{3} + \cos (x)) d x =

und

\int_{1}^{4} x \cdot \sqrt{x} d x =

Aufgabe 1.2.24

Es ist

\int_{- 5}^{5} x \cdot \cos (4 x) d x = 0

, da das Integrationsintervall
bezüglich

0

ist und der Integrand eine
Funktion ist.
Geben Sie in den Felder mit einem Adjektiv passende Eigenschaften an, sodass sich eine richtige Aussage ergibt.

Aufgabe 1.2.25

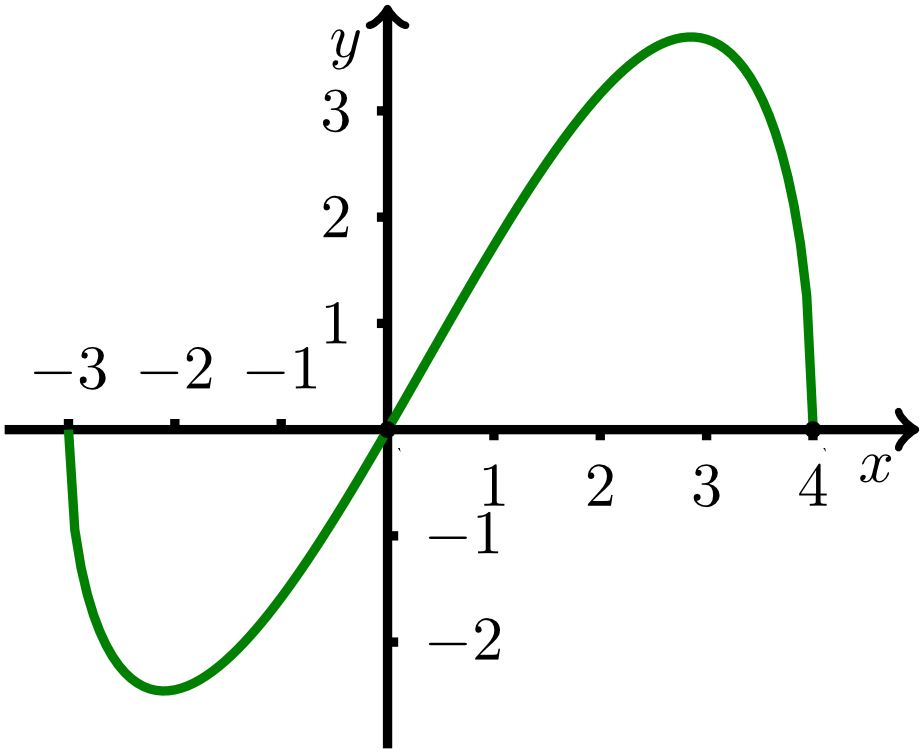
Der Graph der Funktion

f : [- 1; 3] \to ℝ

mit

f (x) : = x^{3} - 3 x^{2} - x + 3

für

- 1 \leq x \leq 3

und die

x

-Achse schließen eine Fläche

A

ein. Berechnen Sie die Schnittpunkte des Graphen von

f

und der

x

-Achse, und bestimmen Sie den Flächeninhalt

I_{A}

von

A

. Antwort:

I_{A} =

Aufgabe 1.2.26

Berechnen Sie den Schnittpunkt der folgenden beiden Geraden:

Die Gerade $y = 3 x + 3$ ,
die Gerade mit der allgemeinen Gleichung $2 x - 2 y = 6$ .

Antwort: Der Schnittpunkt ist .
Geben Sie Punkte in der Form (a;b) ein.

Aufgabe 1.2.27

Ein Kreis habe die allgemeine Kreisgleichung

(x - 1)^{2} + (y + 1)^{2} = d

wobei

d

eine unbekannte positive Konstante ist. Welche Eigenschaften besitzt dieser Kreis?

Sein Radius ist $r$ $=$ .
Sein Mittelpunkt ist $P$ $=$
. Geben Sie Punkte in der Form (a;b) ein.
Er schneidet die durch P=(-3;3) und Q=(3;-3) verlaufende Gerade PQ ‾
- in einem Punkt,
- in zwei Punkten,
- in drei Punkten,
- überhaupt nicht,
- das hängt von der Konstanten $d$ ab.

Aufgabe 1.2.28

Es seien die Vektoren

\vec{x} = (\begin{matrix} 1 \\ 2 \end{matrix}), \vec{y} = (\begin{matrix} 0 \\ - 4 \end{matrix}), \vec{z} = (\begin{matrix} 2 \\ 2 \end{matrix})

gegeben. Berechnen Sie daraus die folgenden Vektoren:

$\vec{x} + \vec{y} - \vec{z}$ $=$ .
$2 \vec{x} - \frac{1}{2} \vec{y}$ $=$ .
$2 (\vec{x} - \vec{y}) + 3 \vec{z}$ $=$ .

Hier erscheint die Testauswertung!

Mathematischer Ausdruck	Gleichung	Ungleichung	Term	Zahl
$\sqrt{3 + \frac{1}{2}}$
$5 x - 1$
$32 x^{2} = \frac{1}{y}$
$32 > 2^{x}$
$x \in {1; 2; 3}$
$b^{2} - 4 a c \geq 0$