Onlinebrückenkurs Mathematik Abschnitt 1.2.1 Graded Test for the Online Course

This is a test for submission:

Unlike open exercises, no hints for formulating mathematical expressions are provided.
The test can be restarted or interrupted at any time.
The test can be terminated and submitted using the buttons at the end of the page, or reset.
The test can be attempted several times. Only the last version will be included in the statistics.

Exercise 1.2.2

Simplify these complex fractions as far as possible:

$1 - \frac{1}{2} + \frac{1}{3} - \frac{1}{4}$ is equivalent to .
$\frac{x - \frac{1}{x}}{1 - \frac{1}{x}}$ is equivalent to .

Exercise 1.2.3

Expand this term completely and collect like terms together:

(a - b) (2 c + d)

=

Exercise 1.2.4

Apply one of the binomial formulas to transform the following terms.The results should not contain any brackets or radical terms.

$(2 \sqrt{3} + x \sqrt{3})^{2}$ = .
$(3 a - 4 b)^{2}$ = .

Exercise 1.2.5

Rewrite these power and radical expressions as a simple power with a rational number as its exponent, without using the root sign:

$\sqrt{a b} \cdot \frac{1}{a} \cdot \sqrt{b^{3}}$ = .
$\sqrt{\sqrt{\sqrt{a} \cdot b} \cdot \frac{1}{c}}$ = .

Exercise 1.2.6

Transform the following fractions such that the denominator disappears. The solution must not contain any fractions or powers.

$\frac{12}{\sqrt{3}}$ = .
$\frac{1 + x - \sqrt{4 x}}{\sqrt{x} - 1}$ = .
$\frac{u^{3}}{\sqrt{u^{2} + 1} + 1}$ = .

If necessary, enter

u^{3}

as u*u*u to avoid the power. Square roots

\sqrt{x}

can be entered as sqrt(x).

Exercise 1.2.7

The single solution of the equation

\frac{x - 2}{| x + 1 |} = \frac{1}{2}

x

=
.

Exercise 1.2.8

Specify the solution sets of the following equations:

$\frac{1}{x} + 2 x = 2 - x$ has the solution set .
$x^{2} - 1 = (x - 1)^{3}$ has the solution set .
$\sqrt[7]{r} = r^{5}$ has the solution set .

Exercise 1.2.9

Find all solutions of the absolute value equation

| 5 x - 1 | = x^{2} - 1

.
The solution set is

L

=

.

Do not use a calculator! Your solution may contain radical terms and fractions.

Exercise 1.2.10

Specify the solution set of the inequality

x^{2} + 6 < - 5 x

as an interval.
The solution interval is
.

Exercise 1.2.11

Specify the solution sets of the following inequalities as intervals. Be careful with the specification of the endpoints.

$(x - 1)^{2} < x$ has the solution set .
$\sqrt{x^{2} - 1} < x$ has the solution set .

Exercise 1.2.12

Find the solution set of the following system of linear equations:

\begin{matrix} - x + 2 y & = & - 5 \\ 3 x + y & = & 1 \end{matrix}

The solution set

	is empty,
	contains exactly one solution: $x =$ , $y =$ ,
	contains an infinite number of solution pairs $(x, y)$ .

Exercise 1.2.13

Find the two-digit number such that its digit sum is 6, and exchanging the digit positions results in a number that is smaller by 18.
Answer:

Exercise 1.2.14

Find the value of the real parameter

α

for which the following system of linear equations

\begin{matrix} 2 x + y & = & 3 \\ 4 x + 2 y & = & α \end{matrix}

has an infinite number of solutions.
Answer:

α =

Exercise 1.2.15

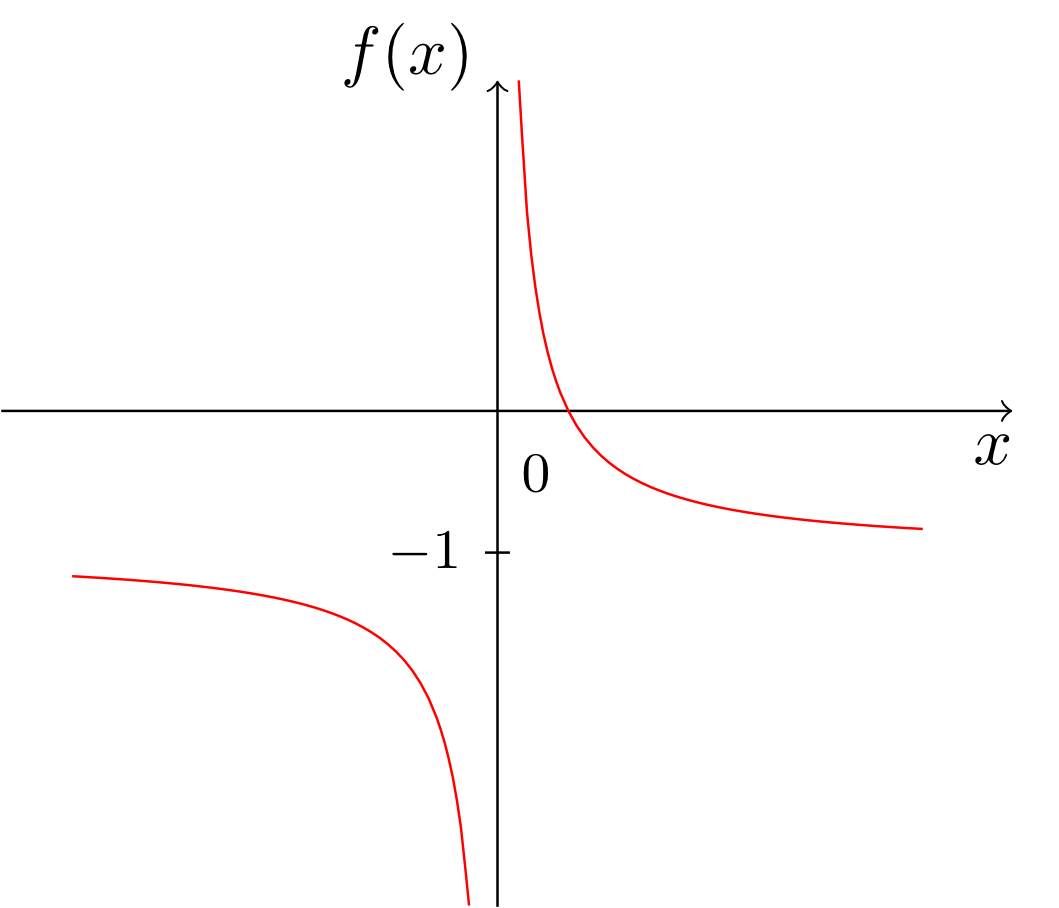
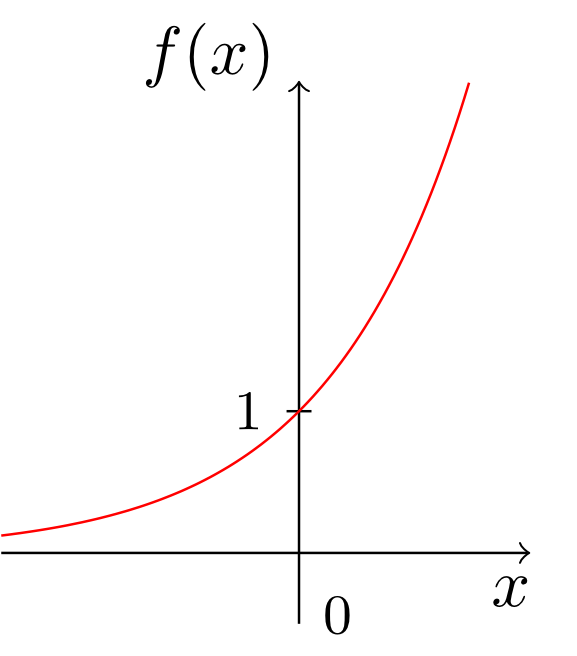
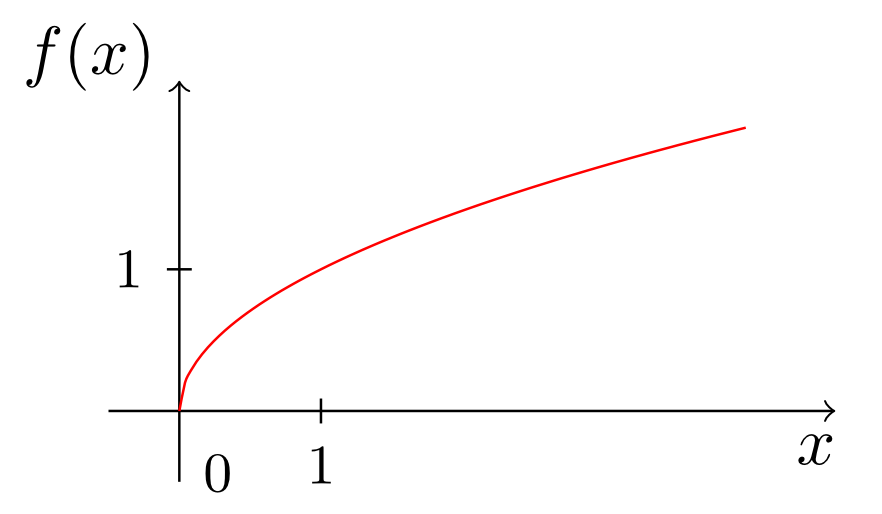
Assign to each of the graphs in (a)-(e) the correct mapping rules of the corresponding functions.

Graph (a) corresponds to the function $f (x)$ $=$ .
Graph (b) corresponds to the function $f (x)$ $=$ .
Graph (c) corresponds to the function $f (x)$ $=$ .
Graph (d) corresponds to the function $f (x)$ $=$ .
Graph (e) corresponds to the function $f (x)$ $=$ .

Select your answers from the mapping rules and input terms listed below (not all of them are used).

$f (x) = \sqrt{x}$	`sqrt(x)`
$f (x) = \frac{1}{2} x - 1$	`(1/2)*x-1`
$f (x) = \ln (1 - x)$	`ln(1-x)`
$f (x) = \ln (x)$	`ln(x)`
$f (x) = x^{1,5}$	`x^(1,5)`
$f (x) = \exp (x) = e^{x}$	`exp(x)`
$f (x) = (0,5)^{x}$	`(0,5)^x`
$f (x) = \frac{1}{x}$	`1/x`
$f (x) = \frac{1}{2 x} - 1$	`1/(2*x)-1`
$f (x) = \frac{1}{2} - x$	`1/x-x`

You can highlight the input terms and drag them into the input boxes.
Specify the asymptote of the function with the mapping rule (a).
It is

lim_{x \to \infty} f (x)

=

Exercise 1.2.16

The figure below shows two lines in two-dimensional space.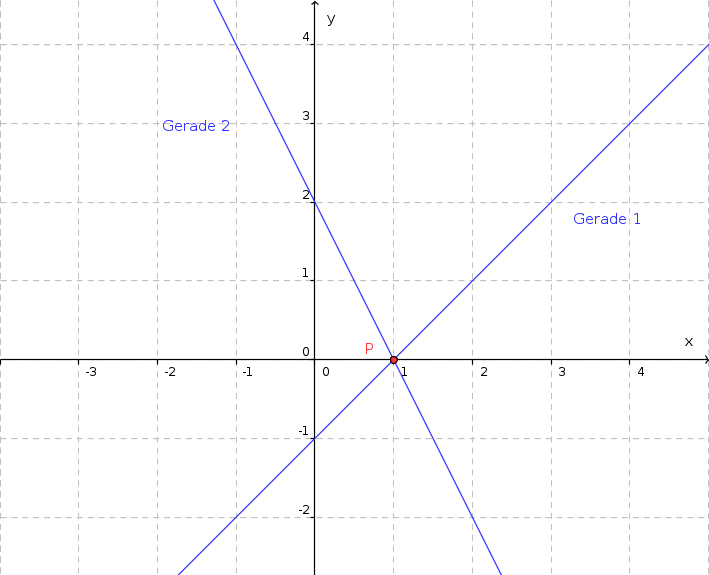

Find the two equations describing the lines.
Line 1:

y =

Line 2:

y =

What is the correct number of solutions to the corresponding system of linear equations?
The system of linear equations has

	no solution,
	exactly one solution, or
	an infinite number of solutions.

Exercise 1.2.17

Find the solution set of the following system of linear equations consisting of three equations in three variables.

\begin{matrix} x + 2 z & = & 3 \\ - x + y + z & = & 1 \\ 2 y + 3 z & = & 5 \end{matrix}

The solution set

	is empty,
	contains exactly one solution: $x =$ , $y =$ , $z =$ ,
	contains an infinite number of solutions $(x, y, z)$ .

Exercise 1.2.18

The mileage counter of a van displays

20

km when the vehicle starts its journey at 6 a.m. Four hours later it arrives at its destination. The odometer is now displaying

280

km. Calculate the average velocity

v

(the average rate of change of position) between the start point and destination. For this purpose, insert the missing numbers and mathematical symbols (

+

-

\cdot

/

) into the following calculation.

v = (280

)

(

- 6) =

Exercise 1.2.19

Consider the function

f : [- 3; 4] \to ℝ

, the graph of which is shown in the figure below.

The derivative at $x_{1} = 4$ is equal to $0$ , not defined, infinite.
The derivative at $x_{2} = 0$ is positive, equal to $0$ , negative.

Exercise 1.2.20

Calculate the first and the second derivative of the function

f : ℝ \to ℝ, x \to \frac{5 x}{3 + x^{2}}

, and give your results with all terms cancelled or collected together as appropriate.

First derivative $f' (x) =$
Second derivative $f'' (x) =$

Enclose the terms in brackets to avoid misinterpretations. Enter, for example,

\frac{x + 1}{(x + 2)^{2}}

as (x+1)/((x+2)^2).

Exercise 1.2.21

Specify the regions on which the function

f

with

f (x) : = \frac{\ln x}{x}

for

x > 0

is monotonically increasing and where it is decreasing. Specify the regions as maximum open intervals

(r, s)

$f$ is monotonically increasing on .
$f$ is monotonically decreasing on .

Enter an open interval as

(a, b)

(a; b)

. Closed intervals can be entered as

[a, b]

[a; b]

. Here,

a

and

b

are allowed to be arbitrary expressions. Do not use the notation

] a, b [

to enter open intervals.
Which of the points

x_{1} = 1

x_{2} = 2

, or

x_{3} = 6

belongs to an interval on which the function

f

is convex?
Answer:

Exercise 1.2.22

Find an antiderivative for each of the following functions.

$\int (5 x^{4} + 8 x) d x =$
$\int 6 \sin (2 x) d x =$

Explicitily denote multiplication by * and use parentheses for the arguments of functions. Example: Polynomial: 3*x + 0.1, sine function: sin(x), Composition of cos and the square root function: cos(sqrt(3*x)).

Exercise 1.2.23

Calculate the integrals

\int_{- \frac{π}{2}}^{\frac{π}{2}} (x^{3} + \cos (x)) d x =

and

\int_{1}^{4} x \cdot \sqrt{x} d x =

Exercise 1.2.24

We have

\int_{- 5}^{5} x \cdot \cos (4 x) d x = 0

since the interval of integration is
with respect to

0

and the integrand is an
function.
Enter into the input boxes adjectives describing the functions properties such that the statement becomes true.

Exercise 1.2.25

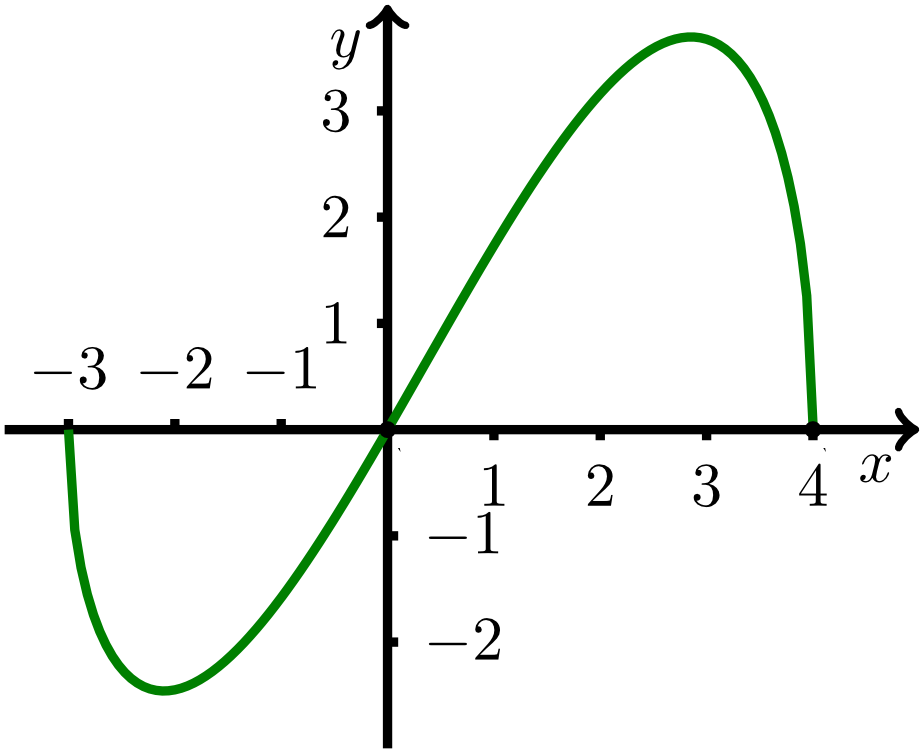
The graph of the function

f : [- 1; 3] \to ℝ

with

f (x) : = x^{3} - 3 x^{2} - x + 3

for

- 1 \leq x \leq 3

and the

x

-axis enclose a region

A

. Specify the intersection points of the graph of

f

with the

x

-axis, and calculate the area

I_{A}

A

. Answer:

I_{A} =

Exercise 1.2.26

Specify the intersection point of the following two lines:

the line $y = 3 x + 3$ ,
the line with the general equation $2 x - 2 y = 6$ .

The intersection point is .
Enter the points in the form (a;b).

Exercise 1.2.27

Let

(x - 1)^{2} + (y + 1)^{2} = d

be the general equation of a circle, where

d

is an unknown positive constant. Specify the properties of this circle.

Its radius is $r$ $=$ .
Its centre is at $P$ $=$
. Enter the points in the form (a;b).
The circle intersects the line PQ ‾ passing trough the points P=(-3;3) and Q=(3;-3)
- at one point,
- at two points,
- at three points,
- not at all,
- the answer depends on the value of the constant $d$ .

Exercise 1.2.28

Take the vectors

\vec{x} = (\begin{matrix} 1 \\ 2 \end{matrix}), \vec{y} = (\begin{matrix} 0 \\ - 4 \end{matrix}), \vec{z} = (\begin{matrix} 2 \\ 2 \end{matrix}) .

From these, calculate the following vectors:

$\vec{x} + \vec{y} - \vec{z}$ $=$ .
$2 \vec{x} - \frac{1}{2} \vec{y}$ $=$ .
$2 (\vec{x} - \vec{y}) + 3 \vec{z}$ $=$ .

The test evaluation will be displayed here!

Mathematical expression	Equation	Inequality	Term	Number
$\sqrt{3 + \frac{1}{2}}$
$5 x - 1$
$32 x^{2} = \frac{1}{y}$
$32 > 2^{x}$
$x \in {1; 2; 3}$
$b^{2} - 4 a c \geq 0$