Kapitel 9 Orientierung im zweidimensionalen Koordinatensystem
Abschnitt 9.3 Kreise in der Ebene9.3.4 Lagebeziehungen für Kreise
Genau wie für zwei Geraden, kann man nun für einen Kreis und eine Gerade oder zwei Kreise die Frage stellen, wie die beiden Objekte relativ zueinander im Koordinatensystem liegen. Dies bedeutet die Frage zu beantworten, ob die beiden Objekte sich schneiden, berühren oder keine Punkte gemeinsam haben. Für einen Kreis und eine Gerade kann man dann eventuelle Schnitt- oder Berührpunkte auch relativ einfach ausrechnen. Für zwei Kreise ist dies schwieriger und geht über den Rahmen dieses Brückenkurses hinaus. Für zwei Kreise wird also nur die Fragestellung behandelt werden, ob sich diese schneiden oder berühren, und nicht, an welchen Punkten dies passiert.Info 9.3.9
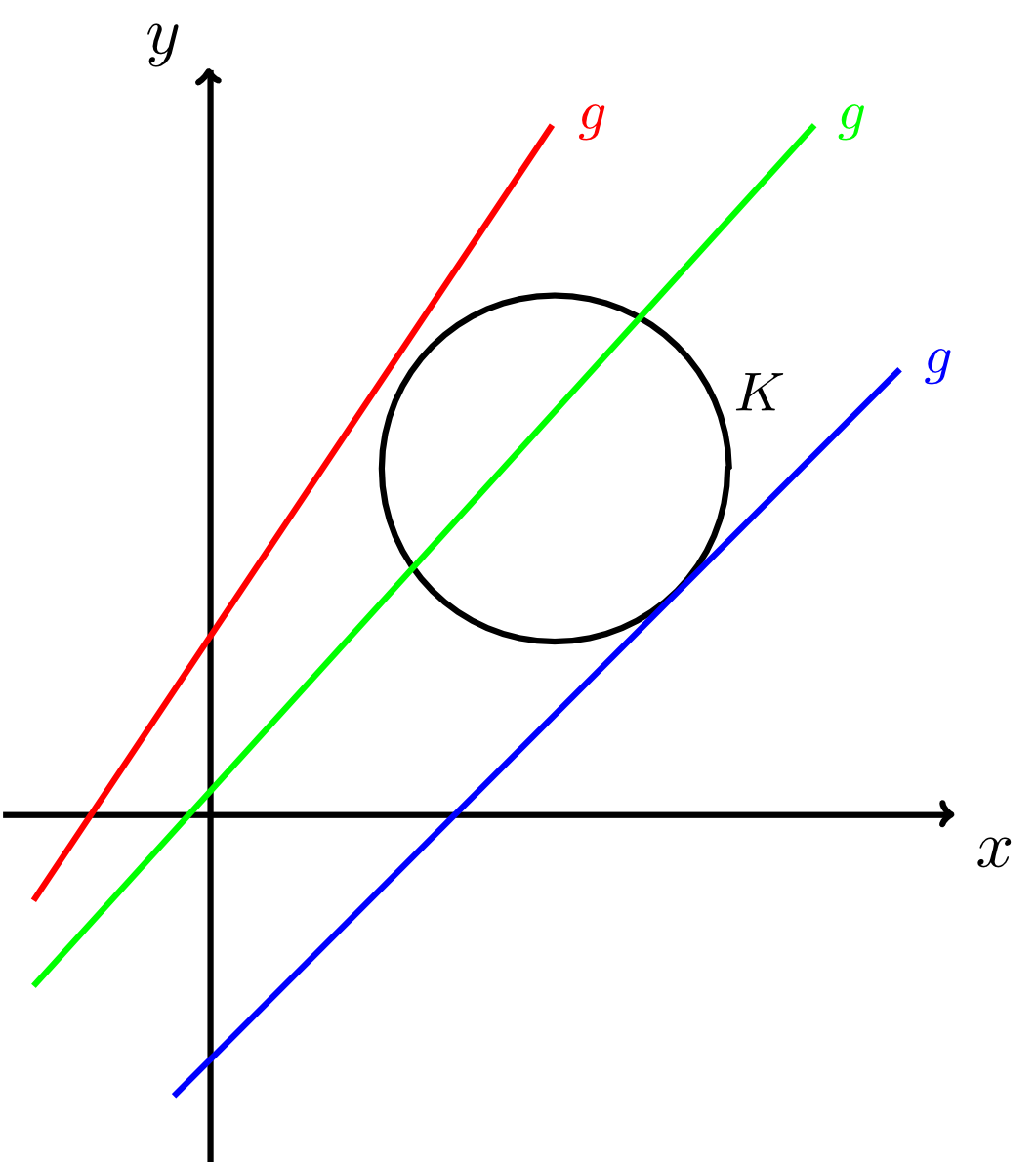
Sind ein Kreis und eine Gerade in der Ebene (durch Koordinatengleichungen bezüglich eines festen Koordinatensystems) gegeben, so gibt es für ihre relative Lage genau drei Fälle:
- Der Kreis und die Gerade haben keine gemeinsamen Punkte. Dies ist für die rote Gerade in der Abbildung unten der Fall. Eine solche Gerade heißt Passante des Kreises.
- Der Kreis und die Gerade haben genau einen Punkt gemeinsam, das heißt die Gerade berührt den Kreis. Dies ist für die blaue Gerade in der Abbildung unten der Fall. Eine solche Gerade heißt Tangente des Kreises.
- Der Kreis und die Gerade haben zwei gemeinsame Punkte, das heißt die Gerade schneidet den Kreis. Dies ist für die grüne Gerade in der Abbildung unten der Fall. Eine solche Gerade heißt Sekante des Kreises.
Im Fall einer Sekante oder Tangente haben Kreis und Gerade also zwei Punkte oder einen Punkt gemeinsam. Wie kann man diesen Punkt oder diese Punkte nun ausrechnen? Da die Punkte jeweils auf Kreis und Gerade liegen, müssen sie sowohl die Koordinatengleichung des Kreises als auch die Koordinatengleichung der Geraden erfüllen. Man hat dann also zwei Gleichungen für die beiden unbekannten Koordinaten der Schnittpunkte und kann diese dadurch ausrechnen. Dabei ist allerdings Folgendes zu beachten: Da in der Koordinatengleichung für Kreise die Unbekannten quadriert vorkommen, handelt es sich nicht um zwei lineare Gleichungen. Es sind also leider nicht die Methoden zum Lösen linearer Gleichungssysteme aus Kapitel 5 anwendbar. Die folgende Infobox fasst die Methode zur Berechnung der Schnittpunkte zusammen.
Info 9.3.10
Sind ein Kreis in der Ebene mit Mittelpunkt und Radius mittels einer Koordinatengleichung
und eine Gerade mit Steigung und Achsenabschnitt in Normalform
gegeben, so kann zur Berechnung eventueller Schnittpunkte, die Gleichung für in die Gleichung für eingesetzt werden. Dies resultiert in einer quadratischen Gleichung in der Variablen :
Für quadratische Gleichungen können bekanntermaßen drei Fälle auftreten (vgl. 2.1.5):
- Die quadratische Gleichung hat keine Lösung. In diesem Fall handelt es sich bei um eine Passante von . Es lässt sich keine -Koordinate eines gemeinsamen Punktes finden.
- Die quadratische Gleichung hat genau eine Lösung. In diesem Fall handelt es sich bei um eine Tangente an . Zu der -Koordinate (der Lösung der quadratischen Gleichung) lässt sich mit Hilfe der Geradengleichung eine zugehörige -Koordinate berechnen. Die beiden Koordinaten zusammen bilden den Berührpunkt der Tangente am Kreis .
- Die quadratische Gleichung hat zwei Lösungen. In diesem Fall handelt es sich bei um eine Sekante von . Zu den beiden -Koordinaten (den Lösungen der quadratischen Gleichung) lassen sich mit Hilfe der Geradengleichung zugehörige -Koordinaten berechnen. Die beiden Koordinatenpaare bilden die Schnittpunkte der Sekante mit dem Kreis .
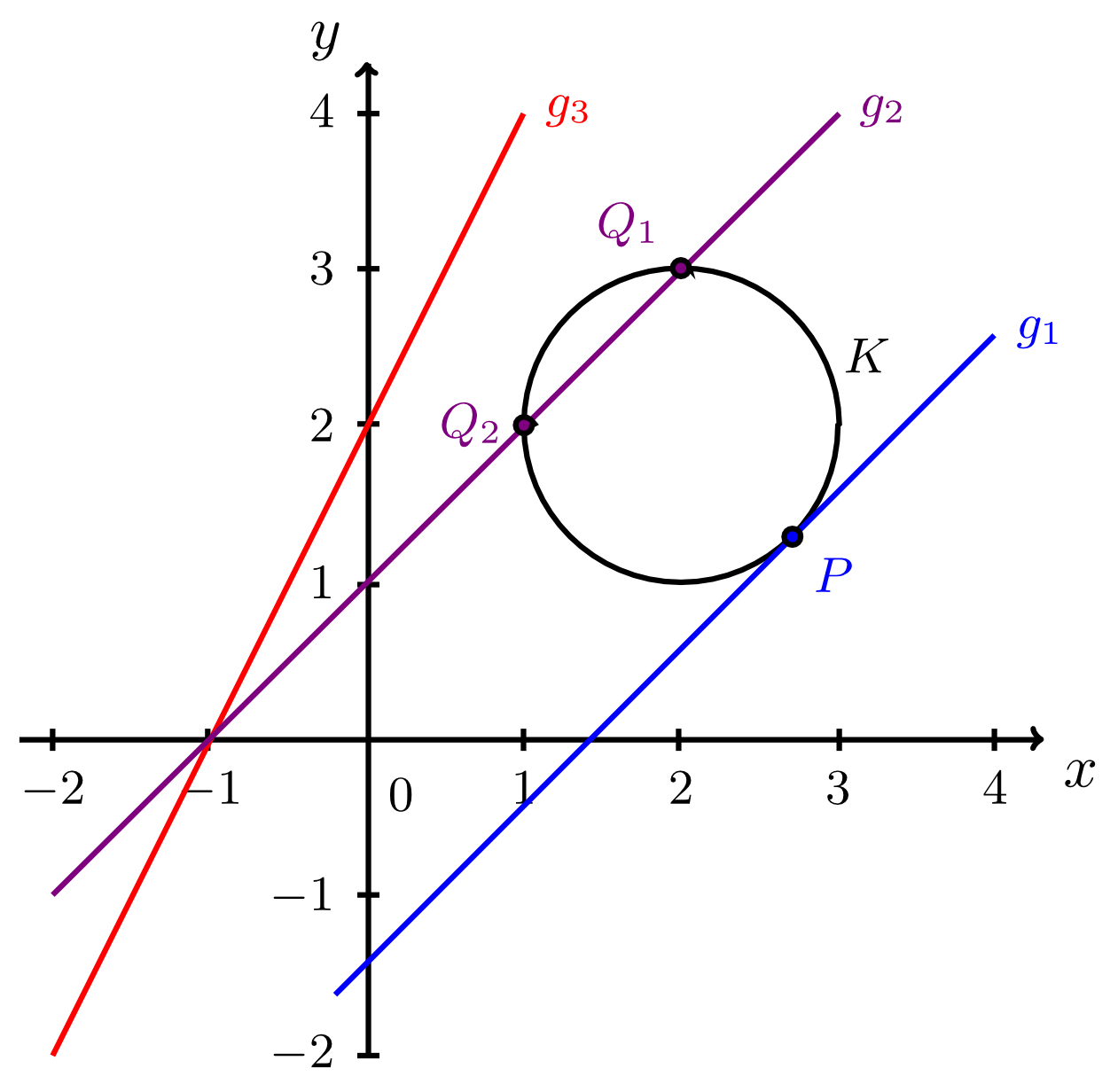
Beispiel 9.3.11
Gegeben sind der Kreis mit Mittelpunkt und Radius durch
sowie die Geraden , und durch
und
sowie die Geraden , und durch
und
- Gerade :
Einsetzen der Geradengleichung in die Kreisgleichung liefert
Die entstehende quadratische Gleichung hat nur die Lösung , womit eine Tangente an ist, welche in einem Punkt mit der -Koordinate berührt. Die zugehörige -Koordinate ist aus der Geradengleichung zu berechnen:
Somit berührt die Tangente den Kreis im Punkt .
- Gerade :
Einsetzen der Geradengleichung in die Kreisgleichung liefert
Die entstehende quadratische Gleichung hat zwei Lösungen, womit eine Sekante des Kreises ist, die in zwei Punkten mit den beiden -Koordinaten und schneidet. Die zugehörigen -Koordinaten berechnen sich aus der Geradengleichung:
Somit sind die Schnittpunkte der Sekanten mit dem Kreis die beiden Punkte und .
- Gerade :
Einsetzen der Geradengleichung in die Kreisgleichung liefert
Die Diskriminante (vgl. 2.1.5) dieser quadratischen Gleichung ist
womit die Gleichung keine Lösung besitzt. Folglich ist die Gerade eine Passante des Kreises .
Aufgabe 9.3.12
Gegeben sind der Kreis durch die Gleichung
sowie die beiden Geraden
und
sowie die beiden Geraden
und
- Zeigen Sie, dass eine Tangente an ist und berechnen Sie - und -Koordinate des Berührpunkts von und .
- Zeigen Sie, dass eine Sekante von ist und berechnen Sie - und -Koordinaten der Schnittpunkte und von und . Sortieren Sie die Schnittpunkte entwsprechend der Größe der -Koordinaten nach.
Aufgabe 9.3.13
Gegeben sind der Kreis durch die Kreisgleichung
und die Gerade mit Steigung und Achsenabschnitt durch die Geradengleichung
in Normalform. Bestimmen Sie das Intervall, in dem der Achsenabschnitt liegen muss, damit eine Sekante von ist.
.
Wurzeln können als sqrt eingegeben werden. Zum Beispiel sqrt(2) für .
und die Gerade mit Steigung und Achsenabschnitt durch die Geradengleichung
in Normalform. Bestimmen Sie das Intervall, in dem der Achsenabschnitt liegen muss, damit eine Sekante von ist.
.
Wurzeln können als sqrt eingegeben werden. Zum Beispiel sqrt(2) für .
Auch Geraden, deren Gleichungen nicht auf Normalform gebracht werden können (also solche, die parallel zur Ordinatenachse verlaufen), können natürlich Kreise schneiden oder berühren. Für diese Geraden ist das oben stehende Verfahren nicht direkt anwendbar. Das Vorgehen in diesem Fall wird im folgenden Beispiel demonstriert.
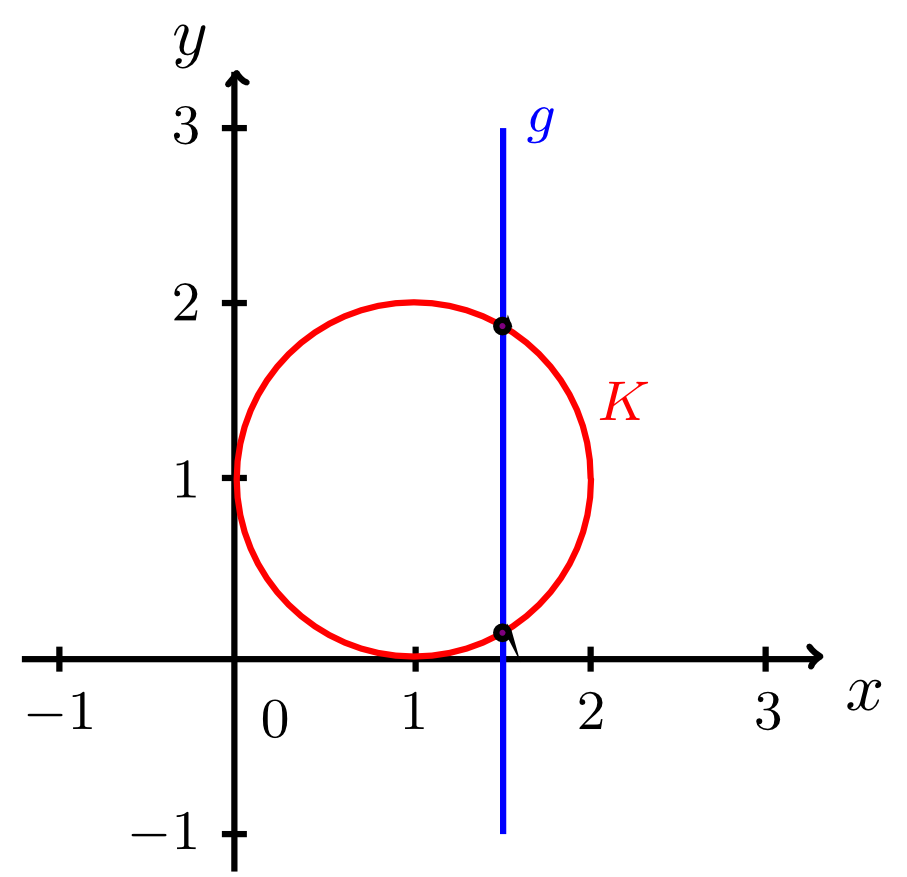
Beispiel 9.3.14
Gegeben sind der Kreis durch die Kreisgleichung
sowie die Gerade durch die Gleichung
Die folgende Abbildung stellt die beiden Objekte dar: Offenbar ist eine Sekante von . Um die Schnittpunkte zu berechnen, kann in diesem Fall die Geradengleichung natürlich nicht nach aufgelöst werden. Stattdessen wird einfach die Geradengleichung für in die Kreisgleichung eingesetzt. Dies liefert zwei -Werte, die -Koordinaten der Schnittpunkte:
Die zugehörigen -Koordinaten sind natürlich beide gleich , da die Schnittpunkte auf der Geraden liegen. Somit ergeben sich die beiden Schnittpunkte und der Geraden und des Kreises .
sowie die Gerade durch die Gleichung
Die folgende Abbildung stellt die beiden Objekte dar: Offenbar ist eine Sekante von . Um die Schnittpunkte zu berechnen, kann in diesem Fall die Geradengleichung natürlich nicht nach aufgelöst werden. Stattdessen wird einfach die Geradengleichung für in die Kreisgleichung eingesetzt. Dies liefert zwei -Werte, die -Koordinaten der Schnittpunkte:
Die zugehörigen -Koordinaten sind natürlich beide gleich , da die Schnittpunkte auf der Geraden liegen. Somit ergeben sich die beiden Schnittpunkte und der Geraden und des Kreises .
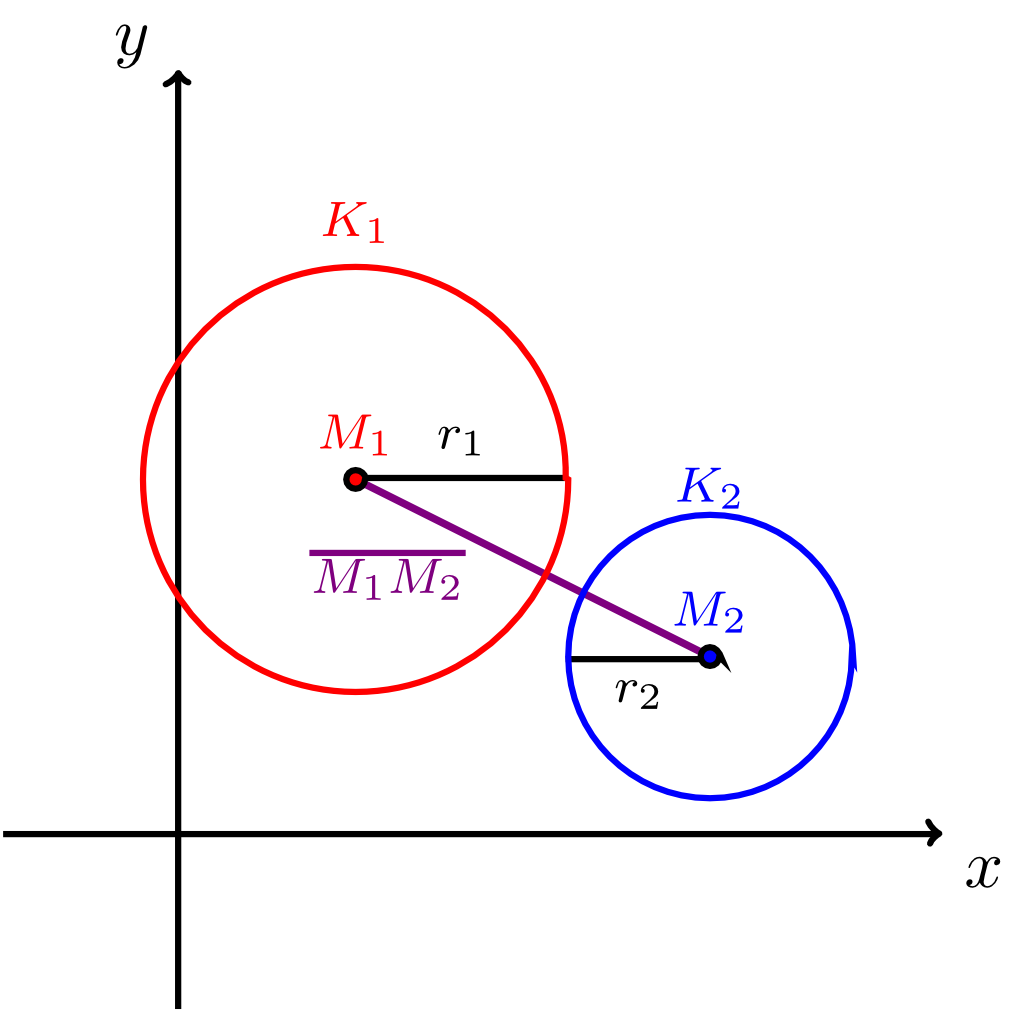
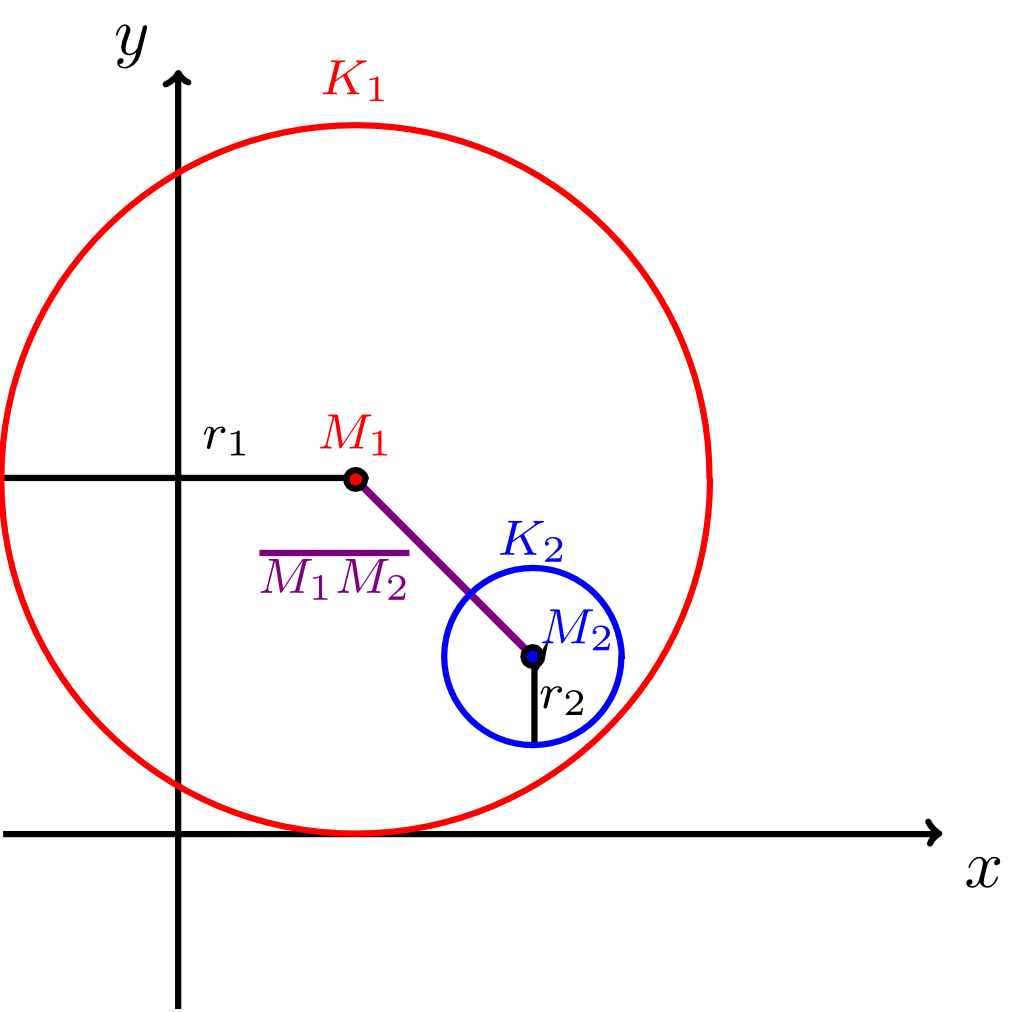
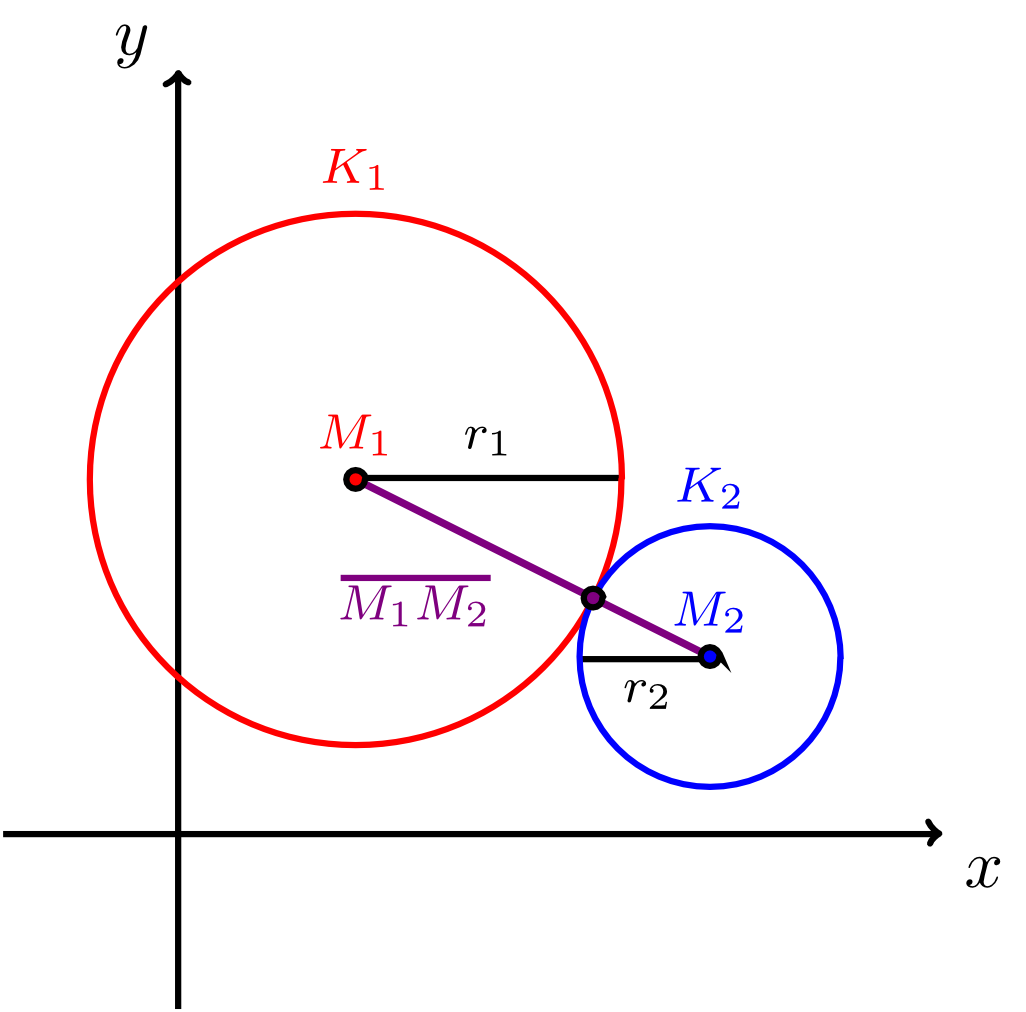
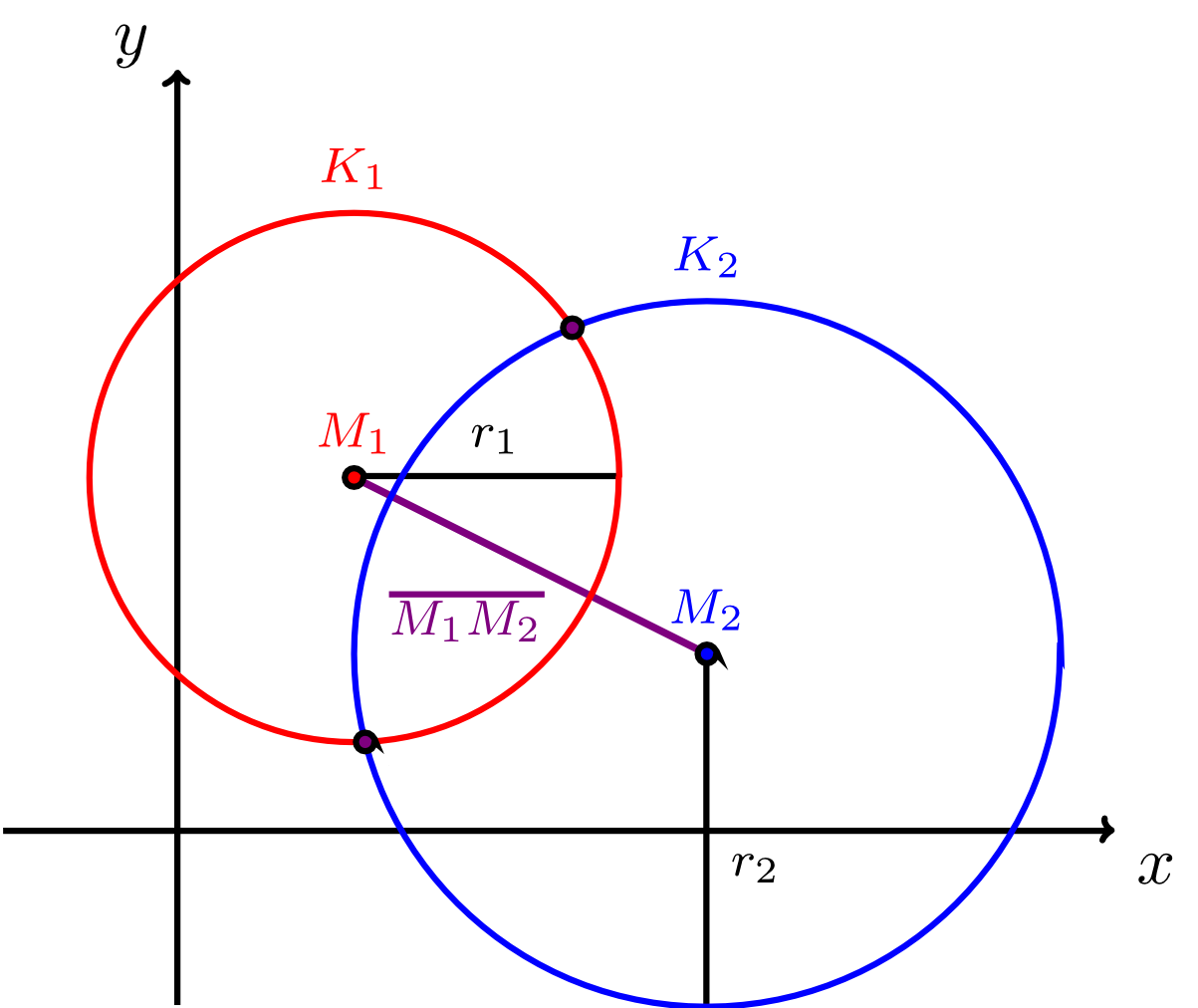
Für die relative Lage zweier Kreise listet die folgende Infobox die möglichen Fälle auf, zusammen mit allgemeinen Kriterien, durch die festgestellt werden kann, welcher Fall für zwei gegebene Kreise jeweils vorliegt.
Info 9.3.15
Sind zwei (verschiedene) Kreise mit dem Mittelpunkt und dem Radius sowie mit dem Mittelpunkt und dem Radius in der Ebene (durch Koordinatengleichungen bezüglich eines festen Koordinatensystems) gegeben, so gibt es für ihre relative Lage genau drei Fälle:
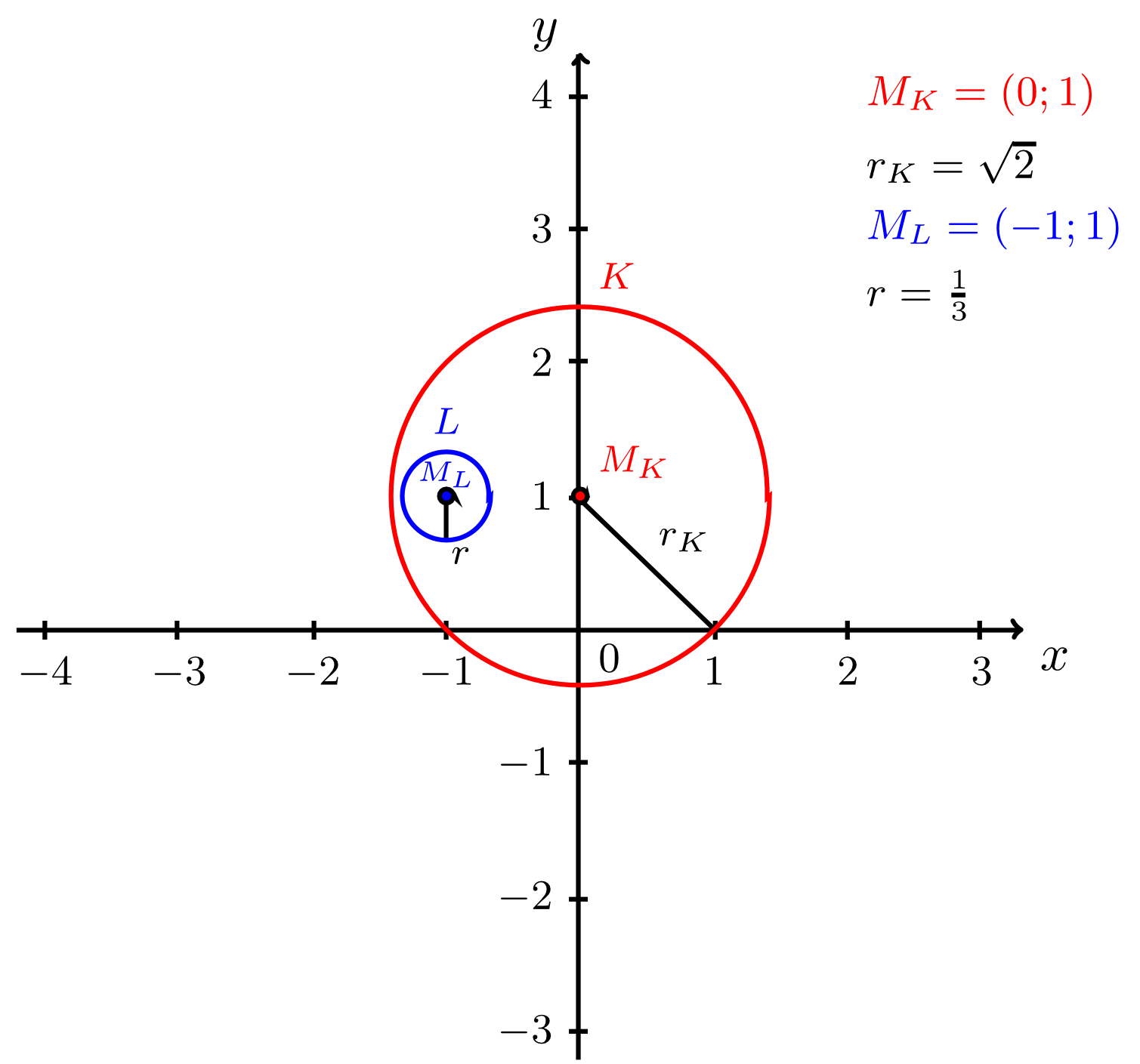
- Die Kreise und haben keine gemeinsamen Punkte, das heißt sie schneiden sich nicht. Dies ist genau dann der Fall wenn für die Radien und sowie für den Abstand der beiden Mittelpunkte gilt:
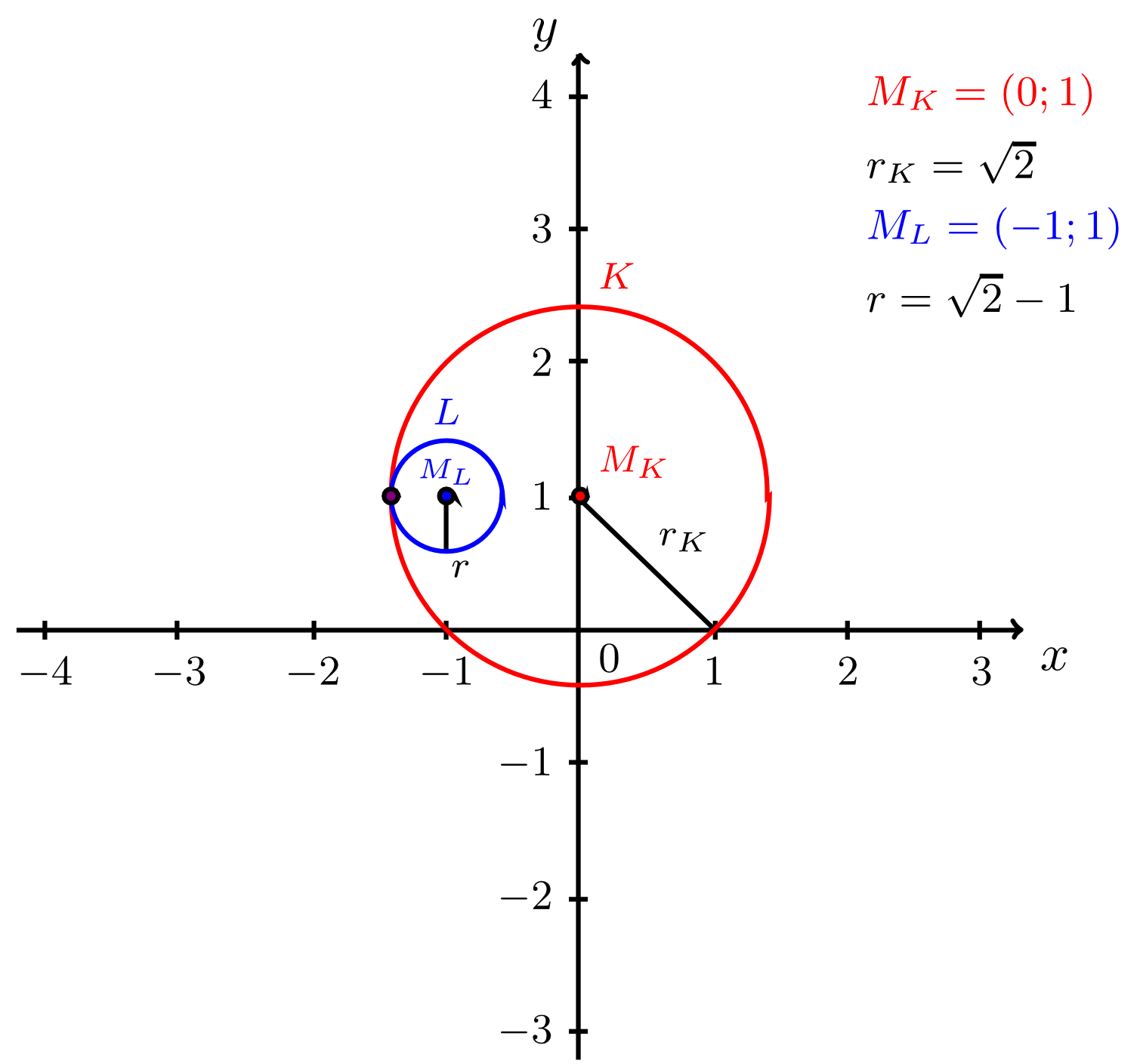
- Die Kreise und haben einen gemeinsamen Punkt, das heißt sie berühren sich. Dies ist genau dann der Fall wenn für die Radien und sowie für den Abstand der beiden Mittelpunkte gilt:
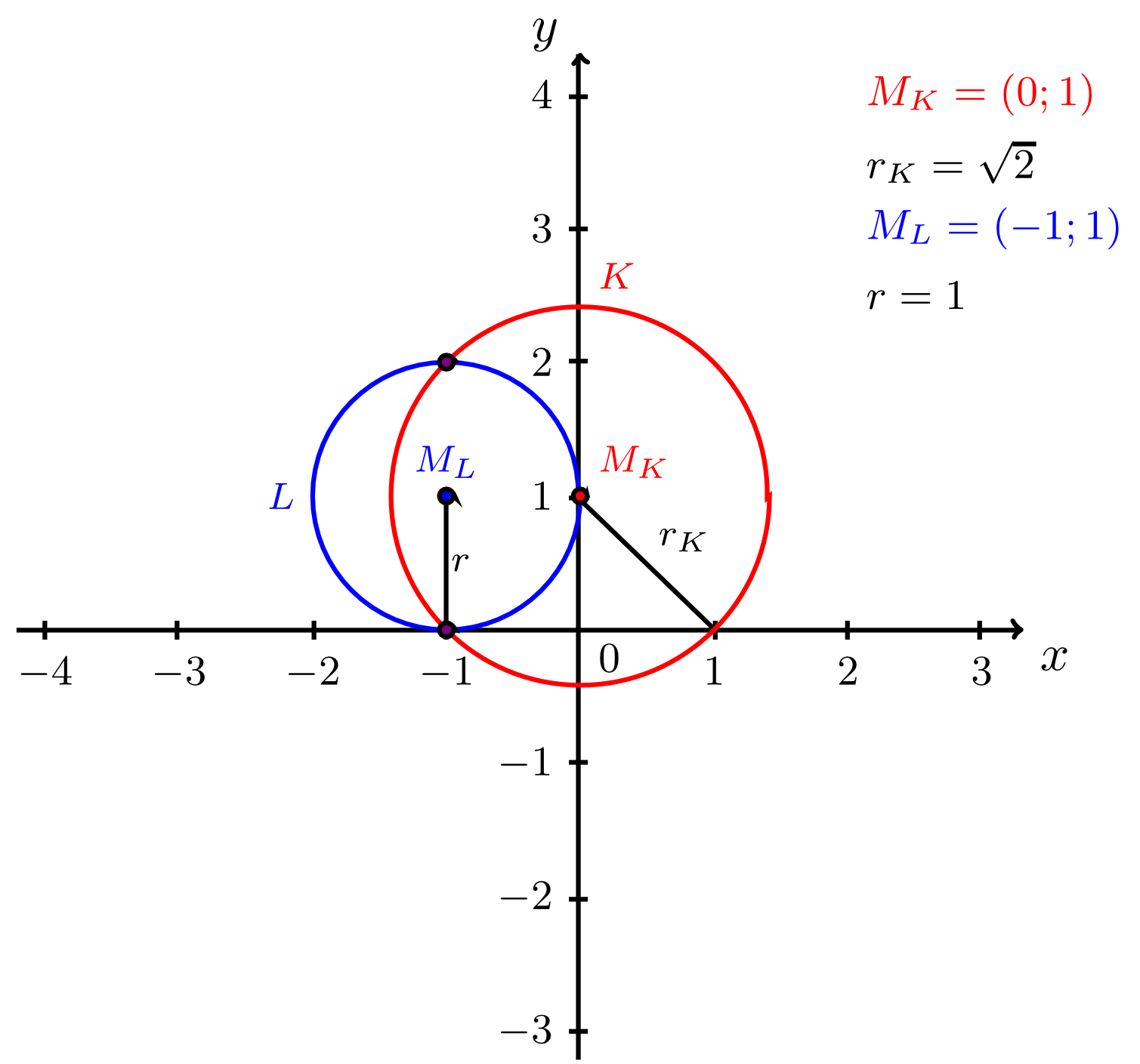
- Die Kreise und haben zwei gemeinsame Punkte, das heißt sie schneiden sich. Dies ist genau dann der Fall wenn für die Radien und sowie für den Abstand der beiden Mittelpunkte gilt:
Beispiel 9.3.16
Gegeben sind ein Kreis mit Mittelpunkt und Radius durch die Gleichung
und ein Kreis mit Mittelpunkt und noch unbekanntem Radius durch die Kreisgleichung
Es sind diejenigen Werte für zu bestimmen, für die die Kreise und sich schneiden, sich berühren bzw. sich nicht schneiden.
Aus der Kreisgleichung für kann der Mittelpunkt direkt abgelesen werden: . Die Kreisgleichung für ist noch nicht in Normalform. Durch quadratische Ergänzung kann diese aber leicht auf Normalform gebracht werden, so dass Mittelpunkt und Radius abgelesen werden können:
Also ist und . Somit beträgt der Abstand der beiden Mittelpunkte
und die Summe der beiden Radien ist
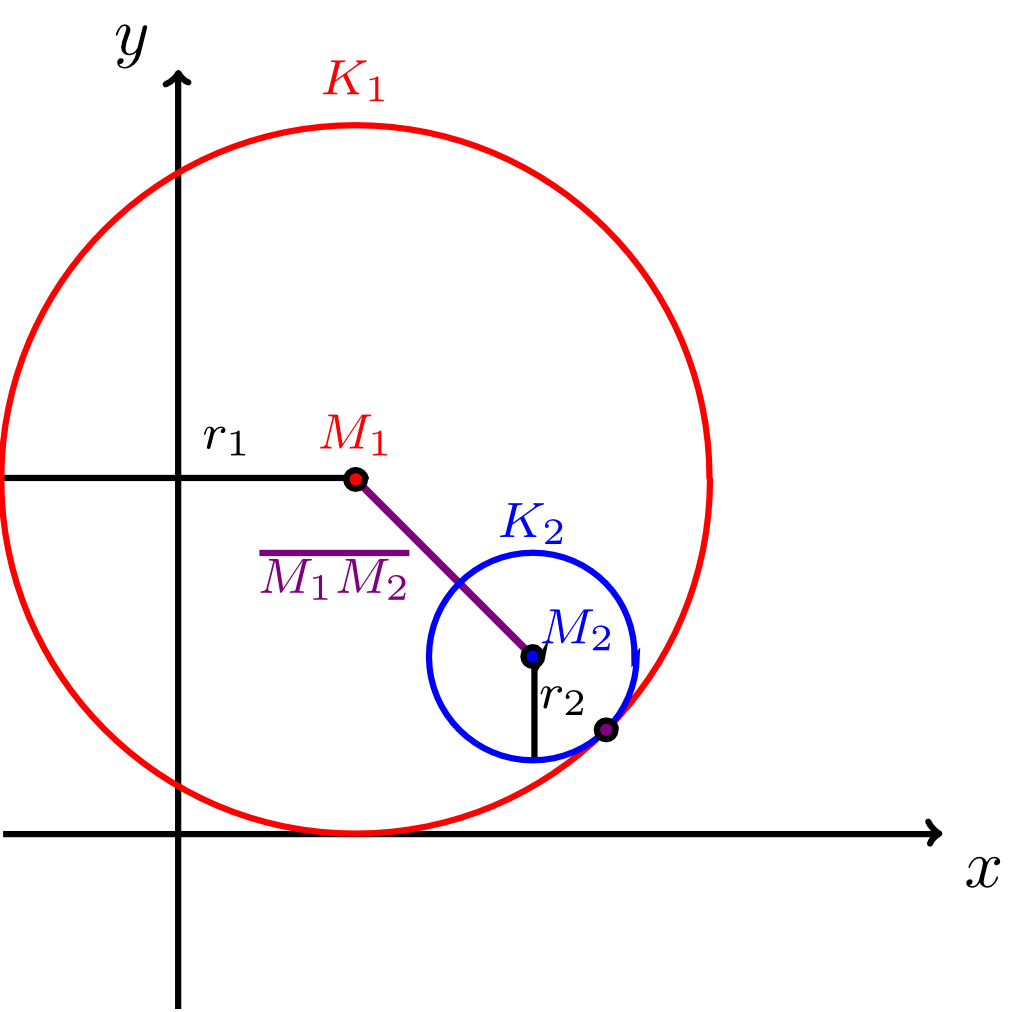
Da gilt, folgt
Somit kann die Situation in diesem Fall nicht eintreten. (Der geometrische Grund hierfür ist, dass der Mittelpunkt von innerhalb des Kreises liegt, wie auch aus der Abbildung unten hervorgeht.) Nach den Kriterien in Infobox 9.3.15 berühren sich die beiden Kreise somit, falls
gilt. Nach dem Abschnitt über Betragsgleichungen, ist diese Gleichung erfüllt, falls
ist. Also sind die beiden Radien , für die der Kreis den Kreis berührt:
Nun sind noch die restlichen möglichen Werte für zu untersuchen. Für gilt
womit und in diesem Fall keine gemeinsamen Punkte besitzen. Für sind zur Untersuchung des Betrags nochmal die Fälle und zu unterscheiden. Im Fall gilt
und auch im Fall gilt
Damit haben und für zwei gemeinsame Punkte, die Kreise schneiden sich also. Zuletzt gilt im Fall :
Somit haben und auch in diesem Fall keine gemeinsamen Punkte. Zusammenfassend erhält man für die relative Lage von und die folgenden Bedingungen:
und ein Kreis mit Mittelpunkt und noch unbekanntem Radius durch die Kreisgleichung
Es sind diejenigen Werte für zu bestimmen, für die die Kreise und sich schneiden, sich berühren bzw. sich nicht schneiden.
Aus der Kreisgleichung für kann der Mittelpunkt direkt abgelesen werden: . Die Kreisgleichung für ist noch nicht in Normalform. Durch quadratische Ergänzung kann diese aber leicht auf Normalform gebracht werden, so dass Mittelpunkt und Radius abgelesen werden können:
Also ist und . Somit beträgt der Abstand der beiden Mittelpunkte
und die Summe der beiden Radien ist
Da gilt, folgt
Somit kann die Situation in diesem Fall nicht eintreten. (Der geometrische Grund hierfür ist, dass der Mittelpunkt von innerhalb des Kreises liegt, wie auch aus der Abbildung unten hervorgeht.) Nach den Kriterien in Infobox 9.3.15 berühren sich die beiden Kreise somit, falls
gilt. Nach dem Abschnitt über Betragsgleichungen, ist diese Gleichung erfüllt, falls
ist. Also sind die beiden Radien , für die der Kreis den Kreis berührt:
Nun sind noch die restlichen möglichen Werte für zu untersuchen. Für gilt
womit und in diesem Fall keine gemeinsamen Punkte besitzen. Für sind zur Untersuchung des Betrags nochmal die Fälle und zu unterscheiden. Im Fall gilt
und auch im Fall gilt
Damit haben und für zwei gemeinsame Punkte, die Kreise schneiden sich also. Zuletzt gilt im Fall :
Somit haben und auch in diesem Fall keine gemeinsamen Punkte. Zusammenfassend erhält man für die relative Lage von und die folgenden Bedingungen:
- Falls gilt, berühren sich die beiden Kreise und in jeweils einem Punkt.
- Falls gilt, schneiden sich die beiden Kreise und in jeweils zwei Punkten.
- Falls gilt, haben die beiden Kreise und keine gemeinsamen Punkte.
Aufgabe 9.3.17
Gegeben sind die beiden Kreise und durch die Gleichungen
und
Die beiden Kreise und
und
Die beiden Kreise und
| berühren sich in einem Punkt, | |
| schneiden sich in zwei Punkten, | |
| haben keine gemeinsamen Punkte. |
 Onlinebrückenkurs Mathematik
Onlinebrückenkurs Mathematik