Chapter 3 Inequalities in one Variable
Section 3.4 Final Test3.4.1 Final Test Module 3
This is a test for submission:- Unlike open exercises, no hints for formulating mathematical expressions are provided.
- The test can be restarted or interrupted at any time.
- The test can be terminated and submitted using the buttons at the end of the page, or reset.
- The test can be attempted several times. Only the last version will be included in the statistics.
Exercise 3.4.1
Find the value of the parameter such that the inequality has exactly one solution:
- The parameter value is .
- In this case
is the only solution of the inequality.
Exercise 3.4.2
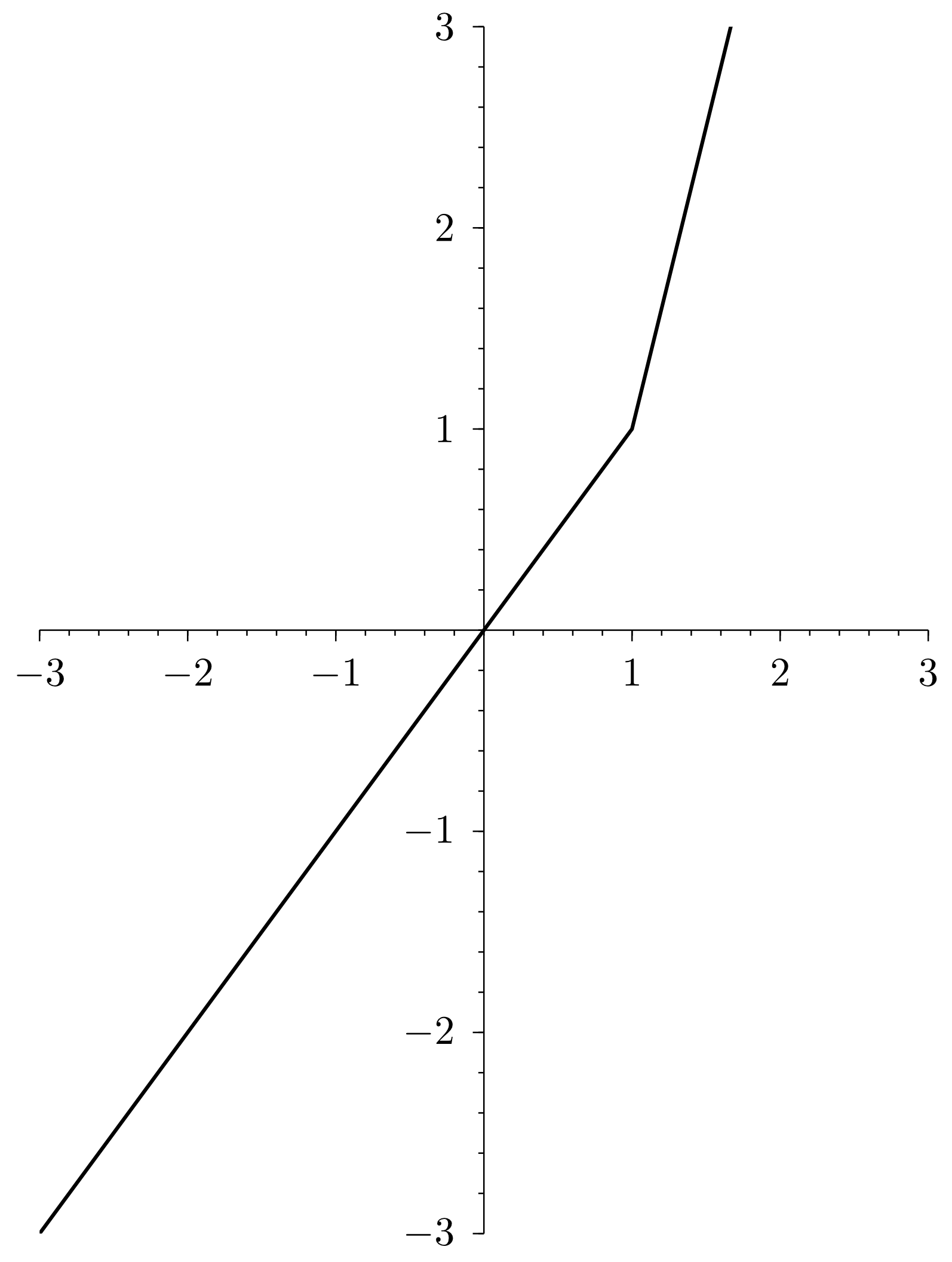
Find an absolute value function describing the following graph as easy as possible.
Try to find a representation of the form . The kink in the graph indicates how the absolute value term looks like.
Try to find a representation of the form . The kink in the graph indicates how the absolute value term looks like.
- Find the solution set of the inequality by means of the graph.
The solution set is .
-
.
Absolute values can be entered in the form betrag(x-a) or abs(x-a).
Exercise 3.4.3
Which positive real numbers satisfy the following inequalities?
- has the solution set
(written as an interval).
- has the solution set
(written as an interval).
The test evaluation will be displayed here!
 Onlinebrückenkurs Mathematik
Onlinebrückenkurs Mathematik