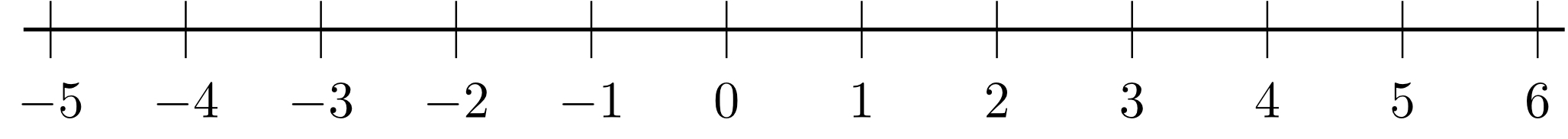Chapter 1 Elementary Arithmetic

Section 1.1 Numbers, Variables, Terms

1.1.1 Introduction

Mathematics is a science in which abstract structures and the logical relations between them are investigated. Before we examine the actual subjects of this section in more detail, we shall refer briefly to the fundamental notion of a set.

Info 1.1.1

We will often be making statements about a number of structurally similar objects. To do so in a compact manner, we can gather such objects into sets that serve as containers for the objects. Let the objects be denoted by

a, b, c, \dots

. Then the symbol

M = {a; b; c; \dots}

denotes the set

M

which has the previously listed objects as its elements. The latter statement is written in short as

a \in M

b \in M

c \in M

etc; thus the symbol "

\in

" reads "is an element of". (Sometimes it is more convenient to reverse the order of element and set. To do so, we can reverse the symbol

\in

, as in

M ∋ a

M ∋ b

M ∋ c

. The meaning is the same as before, and the reversed symbol "

∋

" reads "contains as an element" or just "contains".)
Apart from the list notation for sets, other notations exist. If, for example, the elements have to satisfy a condition

B

, then this is written in the form

T = {x : x satisfies B}

. If

x

is taken (explicitly) from a more comprehensive set

U

, then this is also written in the form

T = {x : x \in U and x satisfies B}

or, in short,

T = {x \in U : x satisfies B}

.
Statements like "

x \in U

" or "

x satisfies B

" are statements in a mathematical sense, i.e. we can assign them a unique truth value "true" or "false". Let

A_{1}

and

A_{2}

be two such statements. In case both

A_{1}

and

A_{2}

hold, we write

A_{1} \land A_{2}

. In case only one of the two statements needs to hold, i.e.

A_{1}

A_{2}

or both, we write

A_{1} \lor A_{2}

.
For two sets

M

and

N

we write:

$M \subseteq N$ , i.e. $M$ is a (possibly improper) subset of $N$ , if every element of $M$ is also an element of $N$ . If at least one element of $N$ exists that is not in $M$ , we say that $M$ is a proper subset of $N$ . In this case we can also write $M \subset N$ .
$M \cup N$ for the union of the two sets. The union denotes the set containing all elements that are contained in at least one of the two sets.
$M \cap N$ for the intersection of the two sets. The intersection denotes the set containing all elements that are contained in both of the two sets.
$N ∖ M$ for the complement, i.e. the set containing all elements of $N$ that are not contained in $M$ .

Thus the union mentioned above is characterised by elements that satisfy the condition

(x \in M) \lor (x \in N)

. However, for the elements of the intersection

(x \in M) \land (x \in N)

holds. In contrast, the complement above contains elements for which

(x \in N) \land (x \notin M)

holds. The symbol

\notin

denotes the negation of the element statement.

To a large extent, mathematics is concerned with the universe of numbers:

\dots; 0; - 3; 4; \frac{4}{5}; \sqrt{2}; e; π; 12.3; 10^{23}; \dots .

However, considering different numbers in more detail reveals fundamental differences. Some numbers cannot be expressed as a closed decimal fraction, others are almost unimaginable (imaginary), still others can be counted on the fingers or can be derived as solutions of equations.

Info 1.1.2

The number ranges used throughout this online course are:

$ℕ = {1; 2; 3; \dots}$	the set of all natural numbers excluding zero,
$ℕ_{0} = {0; 1; 2; 3; \dots}$	the set of all natural numbers including zero,
$ℤ = {\dots; - 2; - 1; 0; 1; 2; \dots}$	the set of all integer numbers (integers),
$ℚ$	the set of all rational numbers (fractions, rationals),
$ℝ$	the set of all real numbers (reals).

These number ranges are not independent of each other. Rather, they form a chain of nested number sets:

ℕ \subset ℕ_{0} \subset ℤ \subset ℚ \subset ℝ .

One obtains these number ranges by examining the solutions of the following equations and extending the number range in such a way that a solution always exists:

Number range	Solvable equation	Unsolvable	Extension by	New range
$ℕ$	$x + 2 = 4$	$x + 2 = 1$	negative numbers	$ℤ$
$ℤ$	$4 x = 20$	$4 x = 5$	fractions	$ℚ$
$ℚ$	$x^{2} = 4$	$x^{2} = 2$	irrational numbers	$ℝ$
$ℝ$	$x^{2} = 2$	$x^{2} = - 1$	etc.

Natural numbers occur whenever numbers of objects have to be determined or things have to be labelled (using numbers). They play a great role in combinatorics: the number of possibilities for selecting 6 balls out of 49 is, for example, a natural number. Natural numbers are the bases of several number systems important either in daily life or in computer science: the binary system has base 2, the decimal system has base 10, and the hexadecimal system has base 16. Specific natural numbers, the prime numbers, are fundamental for modern encryption methods.
Arithmetic on the set of natural numbers is easy, but limits are reached if, for example, you read a temperature value of 3

^{\circ}

C (does it mean plus or minus degrees?) or if an equation such as

x + 5 = 1

needs to be solved. Thus we must extend the set of natural numbers by the negative natural numbers to obtain the set of integers

ℤ

. The set of integers is denoted by

ℤ : = {\dots; - 4; - 3; - 2; - 1; 0; 1; 2; 3; 4; \dots} .

Integers are required whenever the sign (plus or minus) of a natural number matters. In

ℤ

, numbers can be subtracted from each other without any restriction, i.e. systems of equations of the form

a + x = b

are always solvable in

ℤ

(

x = b + (- a)

On the set of integers a comparator

<

can be uniquely defined, so that the integers can be ordered into a chain:

\dots < - 3 < - 2 < - 1 < 0 < 1 < 2 < 3 < \dots .

A rational number (rational) is the ratio of two integers:

Info 1.1.3

The set of rational numbers is denoted by

ℚ : = {\frac{p}{q} : p, q \in ℤ, q \neq 0} .

The elements

\frac{p}{q}

of the set

ℚ

are called fractions, where

p

is the numerator of the fraction and

q

is the non-zero denominator of the fraction.

The rationals play a role whenever the numbers have to be "more precise", e.g. if temperatures have to be given in fractional amounts of

^{\circ}

C, parts of surfaces have to be coloured, or medications have to be mixed from specific ingredients.
Note that the representation as a fraction is not unique: one number can be represented by several fractions. For example,

2 = \frac{4}{2} = \frac{1024}{512}

all represent the same rational number.
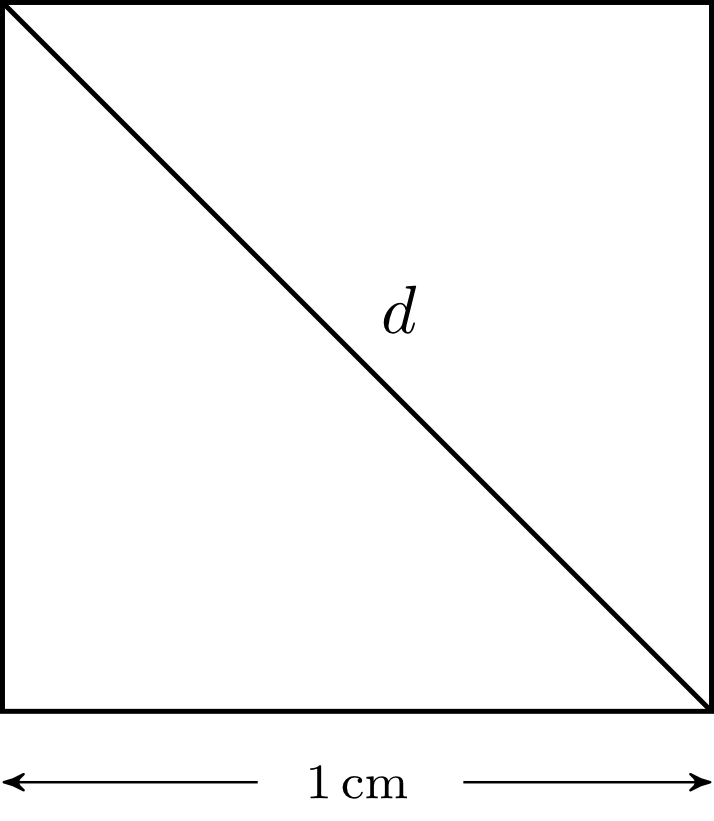
Also, not every number on the number line can be represented as a fraction. Considering, for example, a square with sides of length

1

, the length of the diagonal

d

can be calculated by means of the Pythagoras' theorem:

d^{2} = 1^{2} + 1^{2} = 2, or formally, d = \sqrt{2} .

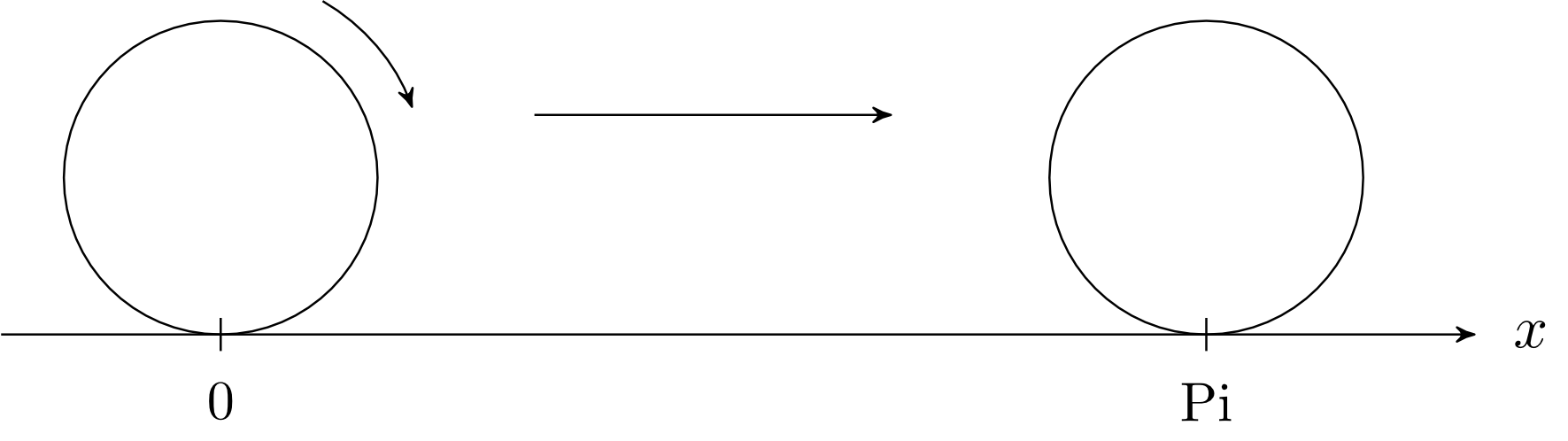
Another number that cannot be represented as a fraction is obtained by unrolling a wheel of diameter

1

on the number line. The result is the number

π

. It can be proven that these two numbers (

\sqrt{2}

and

π

) cannot be represented as fractions. (In the case of

\sqrt{2}

this proof is relatively simple.) These numbers are two examples of the so-called irrational numbers.

A number is irrational if it is not rational, i.e. if it cannot be represented as a fraction. The irrational numbers close the remaining gaps on the number line, where every point now corresponds to exactly one real number.

Info 1.1.4

The set of real numbers is denoted by

ℝ

and includes the set of rational numbers and the set of irrational numbers. It contains all numbers that can be represented on the number line.

Real numbers serve as measures for lengths, areas, temperatures, masses, etc. Throughout this course the mathematical problems are typically solved using real numbers.
A basic property of the real numbers is that they are ordered, i.e. for two reals

a, b

exactly one of the three relations

a < b

a = b

, or

a > b

holds. Another defining property is completeness, which - roughly speaking - describes the "gaplessness" of the number line.

Info 1.1.5

For two different real numbers, one sometimes considers all reals lying between these two numbers on the number line. Such a set of reals is called an interval. An interval is described by assigning a left interval boundary (

a

) and a right interval boundary

(b)

with

a < b

. Depending on whether each interval boundary is included, we must distinguish the following cases:

${x \in ℝ : x \geq a and x \leq b} = [a; b]$ denotes the closed interval between $a$ and $b$ including the interval boundaries.
${x \in ℝ : x > a and x < b} =] a; b [$ denotes the open interval between $a$ and $b$ not including (i.e. excluding) the interval boundaries.
${x \in ℝ : x \geq a and x < b} = [a; b [$ denotes the left-closed and right-open interval between $a$ and $b$ , including the left interval boundary but excluding the right interval boundary.
${x \in ℝ : x > a and x \leq b} =] a; b]$ denotes the left-open and right-closed interval between $a$ and $b$ , including the right interval boundary but excluding the left interval boundary.

The last two intervals are also called half-open intervals.
For open interval ends, unbounded intervals can be considered as well. In these cases the corresponding condition in the set definition is dropped:

{x \in ℝ : x \geq a} = [a; \infty [

{x \in ℝ : x > a} =] a; \infty [

{x \in ℝ : x \leq b} =] - \infty; b]

{x \in ℝ : x < b} =] - \infty; b [

{x \in ℝ} = ℝ =] - \infty; \infty [

.
Moreover, the following descriptions are common:

ℝ^{+} =] 0; \infty [

{ℝ_{0}}^{+} = [0; \infty [

ℝ^{-} =] - \infty; 0 [

{ℝ_{0}}^{-} =] - \infty; 0]

.
A final remark as to the notation: In the literature you will find two different notations for the open end of an interval, either with square brackets pointing outwards or with parentheses, e.g.

[a; b [= [a; b)

] a; b [= (a; b)

. Both notations are correct, don't let them confuse you.

Onlinebrückenkurs Mathematik

1. Elementary Arithmetic

2. Equations in one Variable

3. Inequalities in one Variable

4. System of Linear Equations

5. Geometry

6. Elementary Functions

7. Differential Calculus

8. Integral Calculus

9. Objects in the Two-Dimensional Coordinate System

10. Basic Concepts of Descriptive Vector Geometry

11. Language of Descriptive Statistics