Chapter 1 Elementary Arithmetic

Section 1.1 Numbers, Variables, Terms

1.1.2 Variables and Terms

The use of variables, terms and equations is required to formalise expressions whose values have not been fixed.

Info 1.1.6

A variable is a symbol (typically a letter) used as a placeholder for an indeterminate value. A term is a mathematical expression that can contain variables, arithmetic operations and further symbols and, after substituting variables with numbers, can be evaluated to a specific value. Terms can be combined into equations and inequalities, respectively, or they can be inserted into function descriptions, as we shall see later.

Example 1.1.7

The word problem
In a school class there are four more girls than boys and in total there are 20 children. How many girls and boys are in the class, respectively?
can be formalised, for example, by introducing the variable

a

for the number of girls and the variable

b

for the number of boys in the class and setting up the two equations

a = b + 4

and

a + b = 20

. These equations can be solved by inserting the first equation into the second which gives

a = 12

and

b = 8

. Out of this, the full written answer
In the school class there are $12$ girls and $8$ boys
can be constructed. Here, for example,

b + 4

is a term,

b

itself is a variable, and

a + b = 20

is an equation with a term on the left and a number on the right.

Variables (and sometimes also terms) are generally denoted by Latin lowercase letters

x

y

z

, etc. Often Greek letters are used as well, for example, to distinguish variables that represent angles from those that represent numbers.

Info 1.1.8

This overview shows the (lowercase and uppercase) letters of the Greek alphabet in Greek alphabetical order:

$α$ , $A$	"alpha"	$β$ , $B$	"beta"	$γ$ , $Γ$	"gamma"	$δ$ , $Δ$	"delta"	$ε$ , $E$	"epsilon"
$ζ$ , $Z$	"zeta"	$η$ , $H$	"eta"	$ϑ$ , $Θ$	"theta"	$ι$ , $I$	"iota"	$κ$ , $K$	"kappa"
$λ$ , $Λ$	"lambda"	$μ$ , $M$	"mu"	$ν$ , $N$	"nu"	$ξ$ , $Ξ$	"xi"	$o$ , $O$	"omicron"
$π$ , $Π$	"pi"	$ϱ$ , $P$	"rho"	$σ$ , $Σ$	"sigma"	$τ$ , $T$	"tau"	$υ$ , $ϒ$	"upsilon"
$φ$ , $Φ$	"phi"	$χ$ , $X$	"chi"	$ψ$ , $Ψ$	"psi"	$ω$ , $Ω$	"omega"

In the exercises Greek letters can be entered with their description, e.g. alpha instead of

α

It is important that a term can be evaluated to a specific value if the variables occurring in the term are substituted with numbers:

Example 1.1.9

The following expressions are terms:

$x \cdot (y + z) - 1$ : for $x = 1$ , $y = 2$ , and $z = 0$ one obtains, for example, the value $1$ .
$\sin (α) + \cos (α)$ : for $α = 0^{\circ}$ and $β = 0^{\circ}$ one obtains, for example, the value $1$ (for the calculation of sine and cosine refer to 5).
$1 + 2 + 3 + 4$ : no variables occur, however this is a term (which always gives the value $10$ ).
$\frac{α + β}{1 + γ}$ : for example, $α = 1$ , $β = 2$ , and $γ = 3$ give the value $\frac{3}{4}$ . But $γ = - 1$ is not allowed.
$\sin (π (x + 1))$ : this term, for example, always gives the value zero if $x$ is substituted with an integer.
$z$ : a single variable is also a term.
$1 + 2 + 3 + \dots + (n - 1) + n$ is a term, in which the variable $n$ occurs in the term itself and defines its length as well.

Example 1.1.10

These expressions are not terms in a mathematical sense:

$a + b = 20$ is an equation (inserting values for $a$ and $b$ gives no number, but the equation is simply true or false).
$a \cdot (b + c$ is not correctly bracketed,
"The ratio of girls in the school class" is not a term, but can be formalised by the term $\frac{a}{a + b}$ ,
$\sin$ is not a term but a function name, in contrast $\sin (α)$ is a term (which can be evaluated by inserting an angle for $α$ ).

Exercise 1.1.11

In each question, given a term and number values for the variables that occur in it, what is the evaluation of the term?

$\frac{α + β}{α - β}$ takes the value
for $α = 6$ and $β = 4$ .
$y^{2} + x^{2}$ takes the value
for $y = 2 x + 1$ and $x = - 1$ .
$1 + 2 + 3 + \dots + (n - 1) + n$ takes the value
for $n = 6$ .

After inserting the given values for the variables, the term evaluates to a)

\frac{α + β}{α - β} = \frac{6 + 4}{6 - 4} = \frac{10}{2} = 5

, b)

y^{2} + x^{2} = (- 1)^{2} + (- 1)^{2} = 2

, and c)

1 + 2 + 3 + 4 + 5 + 6 = 21

Exercise 1.1.12

Formalise, using the variables given, the proportion of girls and the proportion of boys, the number of girls being denoted by the variable

a

and the number of boys by the variable

b

:
The proportion of girls is
and the proportion of boys is .
Fractions can be entered using the slash (above the 7-key on most keyboards), where numerator and denominator, respectively, should be bracketed if arithmetic operations occur. The fraction

\frac{1 + x}{2 + y}

can be entered, for example, by (1+x)/(2+y).

The total number of children is

a + b

, hence the proportion of girls is

\frac{a}{a + b}

and the proportion of boys is

\frac{b}{a + b}

Terms can be inserted into other terms as well:

Info 1.1.13

When inserting terms, a term is substituted for a symbol in another term. If the term to be inserted contains several expressions, the replaced symbol has to be bracketed in advance.

Example 1.1.14

Substituting, for example, the right-hand side of

x = 1 + 2 + 3

into the term

x^{2} + y^{2}

results in the new term

x^{2} + y^{2} = (1 + 2 + 3)^{2} + y^{2} = 36 + y^{2}

and certainly not

1 + 2 + 3^{2} + y^{2} = 12 + y^{2}

Exercise 1.1.15

Which term is formed if the following object is inserted into the term

x^{2} + y^{2}

The angle $α$ both for $x$ and $y$ : Then $x^{2} + y^{2}$ $=$ .
The number $2$ for $y$ and the term $t + 1$ for $x$ : Then $x^{2} + y^{2}$ $=$ .
The term $z + 1$ for $x$ and the term $z - 1$ for $y$ : Then $x^{2} + y^{2}$ $=$ .

The Greek letter

α

can be entered as alpha.

It is safest to bracket the variables before inserting, if the new term contains several symbols:

$x^{2} + y^{2} = α^{2} + α^{2} = 2 α^{2}$ .
$x^{2} + y^{2} = (x)^{2} + y^{2} = (t + 1)^{2} + 2^{2} = t^{2} + 2 t + 5$ .
$x^{2} + y^{2} = (x)^{2} + (y)^{2} = (z + 1)^{2} + (z - 1)^{2} = z^{2} + 2 z + 1 + z^{2} - 2 z + 1 = 2 z^{2} + 2$ .

Exercise 1.1.16

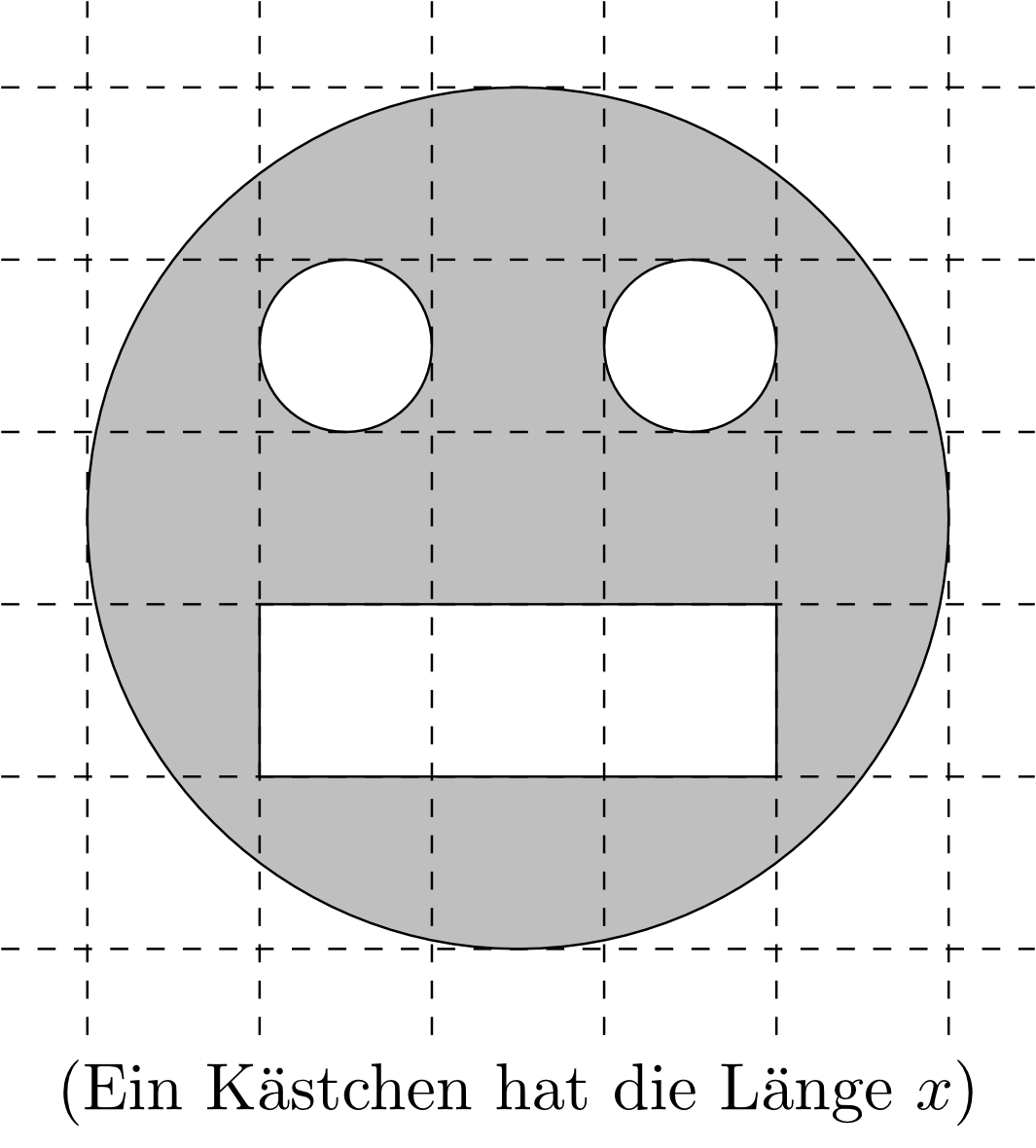
In the following figure, a square on the paper has side length

x

. What is the area of this figure (as a term in the variable

x

A figure on squared paper.

Answer:

The large circle has a total area of ,
each smaller circle has an area of ,
the total area of the figure is .

The number

π

can be entered as pi.

The calculation of areas is presented in later chapters. To solve this exercise, you only need to know that a rectangle of side lengths

a

and

b

has the area

a \cdot b

(entered as a*b) and a circle of radius

r

has the area

π r^{2}

(entered as pi*r^2).

The large circle has in total the area

\frac{25}{4} π x^{2}

(entered as 25/4*pi*x*x). Each smaller circle has the area

\frac{1}{4} π x^{2}

, and the whole figure has the area

(\frac{25}{4} π - \frac{1}{2} π - 3) \cdot x^{2}

Onlinebrückenkurs Mathematik

1. Elementary Arithmetic

2. Equations in one Variable

3. Inequalities in one Variable

4. System of Linear Equations

5. Geometry

6. Elementary Functions

7. Differential Calculus

8. Integral Calculus

9. Objects in the Two-Dimensional Coordinate System

10. Basic Concepts of Descriptive Vector Geometry

11. Language of Descriptive Statistics