Chapter 1 Elementary Arithmetic

Section 1.3 Transformation of terms

1.3.4 Representation as a Sum and as a Product

Mathematical expressions can be written in different ways that all have their own pros and cons. We distinguish them based on which mathematical operation is to be performed last. The most common types are the representation as a sum and the representation as a product.

Info 1.3.14

For a representation as a product, it is the multiplication that is performed last. Because of the order of operation rule, if any of the factors involves an addition or subtraction, then having the multiplication be last can only be achieved by enclosing the factors in brackets. Product is particularly useful for determining cases in which a term takes the value zero. This happens if and only if one of the factors takes the value zero.

For example, the term

(x - 1) \cdot (x - 2)

is zero if

x = 1

x = 2

. For all other values of

x

the term takes a non-zero value.

Info 1.3.15

For a representation as a sum it is the addition or the subtraction that is performed last. Because of the order of operation rule, terms without brackets are automatically in this representation, provided they contain any addition or subtraction at all. From the representation as a sum the asymptotic behaviour of an expression can often be deduced. The asymptotic behaviour of a function describes how the function behaves if the variable

x

takes arbitrarily large values. For polynomials, for example, the asymptotic behaviour is determined by the term with the largest exponent.

To change from one representation to another, several methods exist.

Info 1.3.16

Expanding means multiplying each summand of one factor by each summand of the other factor and adding up the results. In case of more than two factors, they should be multiplied out step by step (only two at a time).

Example 1.3.17

The function

f (x) = (x + 3) (x - 2) (x + 1)

is multiplied out as follows:

\begin{matrix} f (x) & = & (x + 3) \cdot (x - 2) \cdot (x + 1) \\ = & (x^{2} + 3 x - 2 x - 6) \cdot (x + 1) \\ = & (x^{2} + x - 6) \cdot (x + 1) \\ = & x^{3} + x^{2} - 6 x + x^{2} + x - 6 \\ = & x^{3} + 2 x^{2} - 5 x - 6 . \end{matrix}

Exercise 1.3.18

Expand the following terms completely and collect like terms. Describe the asymptotic behaviour of the final expression:

$f (x) = (3 - x) (x + 1)$ =
.

$(3 - x) (x + 1) = 3 x + 3 - x^{2} - x = 3 + 2 x - x^{2}$

Description of the asymptotic behaviour:
As $x$ approaches $\infty$ the function $f (x)$ approaches
.
If the asymptotic behaviour arises uniquely it can be described for short using the symbol "lim":

$lim_{x \to \infty} f (x) = - \infty .$

As $x$ approaches $- \infty$ the function $f (x)$ approaches
.

In this case we have

$lim_{x \to - \infty} f (x) = - \infty .$

You can enter limits $\infty$ and asymptotes as unendlich or infinity, likewise -unendlich or infinity for $- \infty$ . the asymptotic behaviour will be explained in a later chapter of this module. If you are not familiar with the symbols you can skip this exercise part.
$(x + 4) (2 - x) (x + 2)$ =
.

$(x + 4) (2 - x) (x + 2) = (x + 4) (4 - x^{4}) = 4 x - x^{3} + 16 - 4 x^{2} = 16 + 4 x - 4 x^{2} - x^{3}$
$(3 - x) (x + 1)^{2}$ =
.

$(3 - x) (x + 1)^{2} = (3 - x) (x^{2} + 2 x + 1) = 3 x^{2} + 6 x + 3 - x^{3} - 2 x^{2} - x = 3 + 5 x + x^{2} - x^{3}$
$t \cdot (t + 1) \cdot (t^{2} + t + 1)$ =
.

$t \cdot (t + 1) \cdot (t^{2} + t + 1) = (t^{2} + t) (t^{2} + t + 1) = t^{4} + t^{3} + t^{2} + t^{3} + t^{2} + t = t^{4} + 2 t^{3} + 2 t^{2} + t$

Expanding gives

f (x) = (3 - x) (x + 1) = - x^{2} + 2 x + 3

. The leading term is

- x^{2}

. Thus the graph of the function is a parabola opening downwards with the two asymptotes

- \infty

for

x

approaching

\pm \infty

lim_{x \to \infty} f (x) = - \infty, lim_{x \to - \infty} f (x) = - \infty .

In the other parts of this exercise we get by expanding

\begin{matrix} (x + 4) (2 - x) (x + 2) & = & - x^{3} - 4 x^{2} + 4 x + 16, \\ (3 - x) (x + 1)^{2} & = & (3 - x) (x^{2} + 2 x + 1) = - x^{3} + x^{2} + 5 x + 3, \\ t \cdot (t + 1) \cdot (t^{2} + t + 1) & = & t \cdot (t^{3} + 2 t^{2} + 2 t + 1) = t^{4} + 2 t^{3} + 2 t^{2} + t . \end{matrix}

Exercise 1.3.19

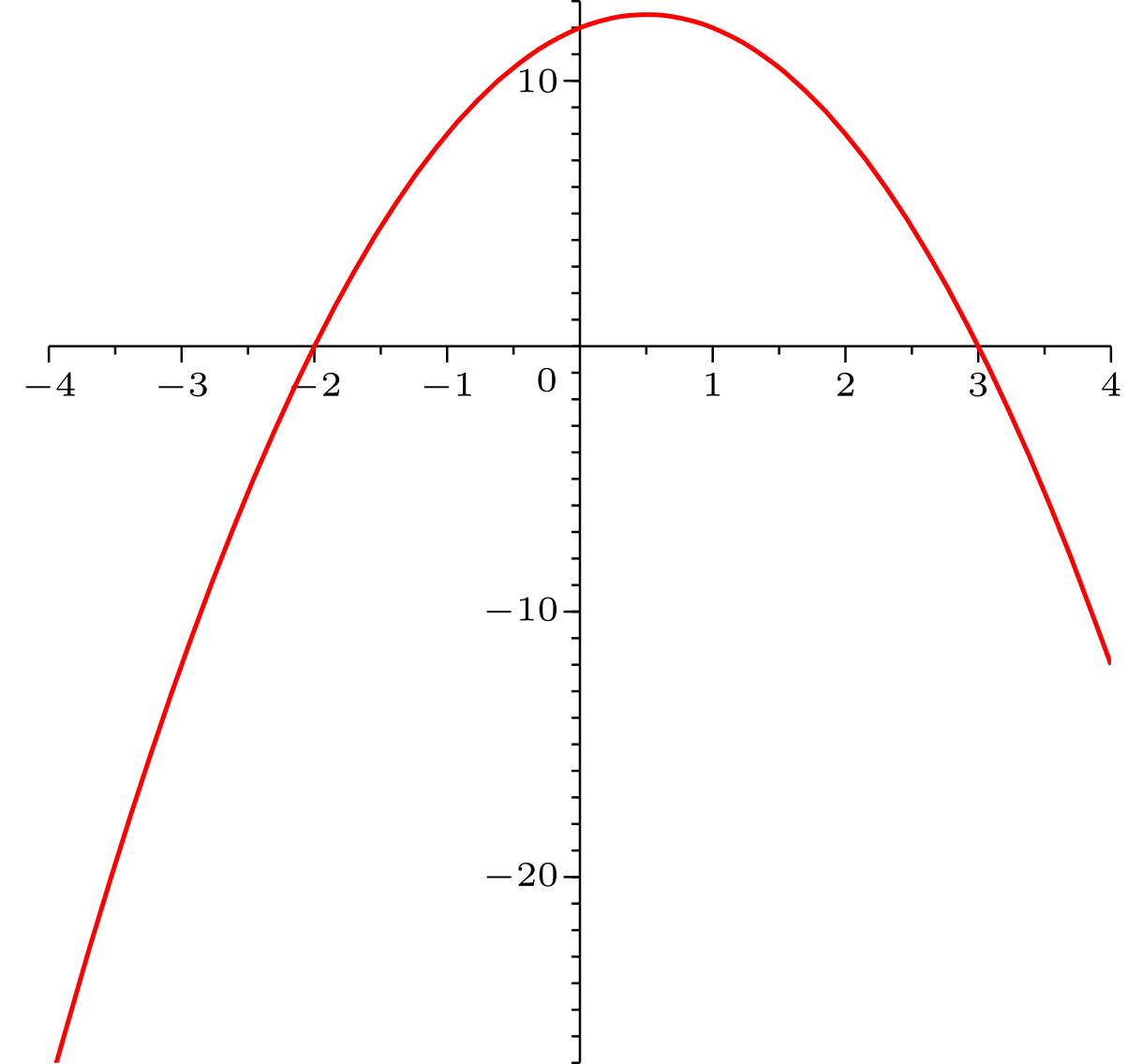
The following graph corresponds to a polynomial

g (x)

of degree two:

Graph of the function

g (x)

From the graph, derive the representation of

g (x)

as a product.

The graph has two zeros $x_{1}$ and $x_{2}$ . Multiplied out the two factors resulting from this fact, we get the polynomial $f (x) = (x - x_{1}) (x - x_{2})$ = .
The polynomial $f (x)$ does not correspond to the graph since at $x = 0$ it takes the value
whereas the graph shows that the function $g (x)$ at $x = 0$ takes the value
. This difference can be corrected by setting $g (x) = c \cdot f (x)$ , where $c$ = .
This finally gives the representation of $g (x)$ as a product: $g (x)$ = .

The graph shows the zeros

x_{1} = - 2

and

x_{2} = 3

. Multiplying out the two factors resulting from this fact, we get the polynomial

f (x) = (x + 2) (x - 3) = x^{2} - x - 6

. At

x = 0

, we have

f (0) = - 6

, but the graph shows

g (0) = 12

. This difference can be corrected by an additional factor of

- 2

. In total, we have

g (x) = - 2 x^{2} + 2 x + 12

Exercise 1.3.20

Fully expand the expression:

(a + 2 b + 3 c)^{2}

= .

It is simplest to multiply each summand in the first pair of brackets by each summand in the second, finally collecting like terms:

\begin{matrix} (a + 2 b + 3 c)^{2} & = & (a + 2 b + 3 c) \cdot (a + 2 b + 3 c) \\ = & a^{2} + 2 a b + 3 a c + 2 a b + 4 b^{2} + 6 b c + 3 a c + 6 b c + 9 c^{2} \\ = & a^{2} + 4 a b + 6 a c + 4 b^{2} + 12 b c + 9 c^{2} . \end{matrix}

Onlinebrückenkurs Mathematik

1. Elementary Arithmetic

2. Equations in one Variable

3. Inequalities in one Variable

4. System of Linear Equations

5. Geometry

6. Elementary Functions

7. Differential Calculus

8. Integral Calculus

9. Objects in the Two-Dimensional Coordinate System

10. Basic Concepts of Descriptive Vector Geometry

11. Language of Descriptive Statistics