Chapter 11 Language of Descriptive Statistics

Section 11.1 Terminology and Language

11.1.2 Rounding

The rounding of measurement values is an everyday process.

Info 11.1.3

In principle, there are three ways of rounding:

Rounding (off) using the $floor$ function $⌊ x ⌋$ .
Rounding (up) using the $ceil$ function $⌈ x ⌉$ .
Rounding using the $round$ function (sometimes also called $rnd$ function).

The $floor$ function is defined as

floor : ℝ \to ℝ, x ⟼ floor (x) = ⌊ x ⌋ = max {k \in ℤ : k \leq x} .

x \in ℝ

is a real number, then

floor (x) = ⌊ x ⌋

is the largest integer that is smaller than or equal to

x

. It results from rounding off the value of

x

. If a positive real number

x

is written as a decimal, then

⌊ x ⌋

equals the integer on the left of the decimal point: rounding (off) cuts off the digits on the right of the decimal point. For example

⌊ 3.142 ⌋ = 3

but

⌊ - 2.124 ⌋ = - 3

. The

floor

function is a step function with jumps (in more mathematical terms, jump discontinuities) of height

1

at all points

x \in ℤ

. The function values at the jumps always lie a step up. They are indicated by the small circles in the figure below, which shows the graph of the

floor

function.

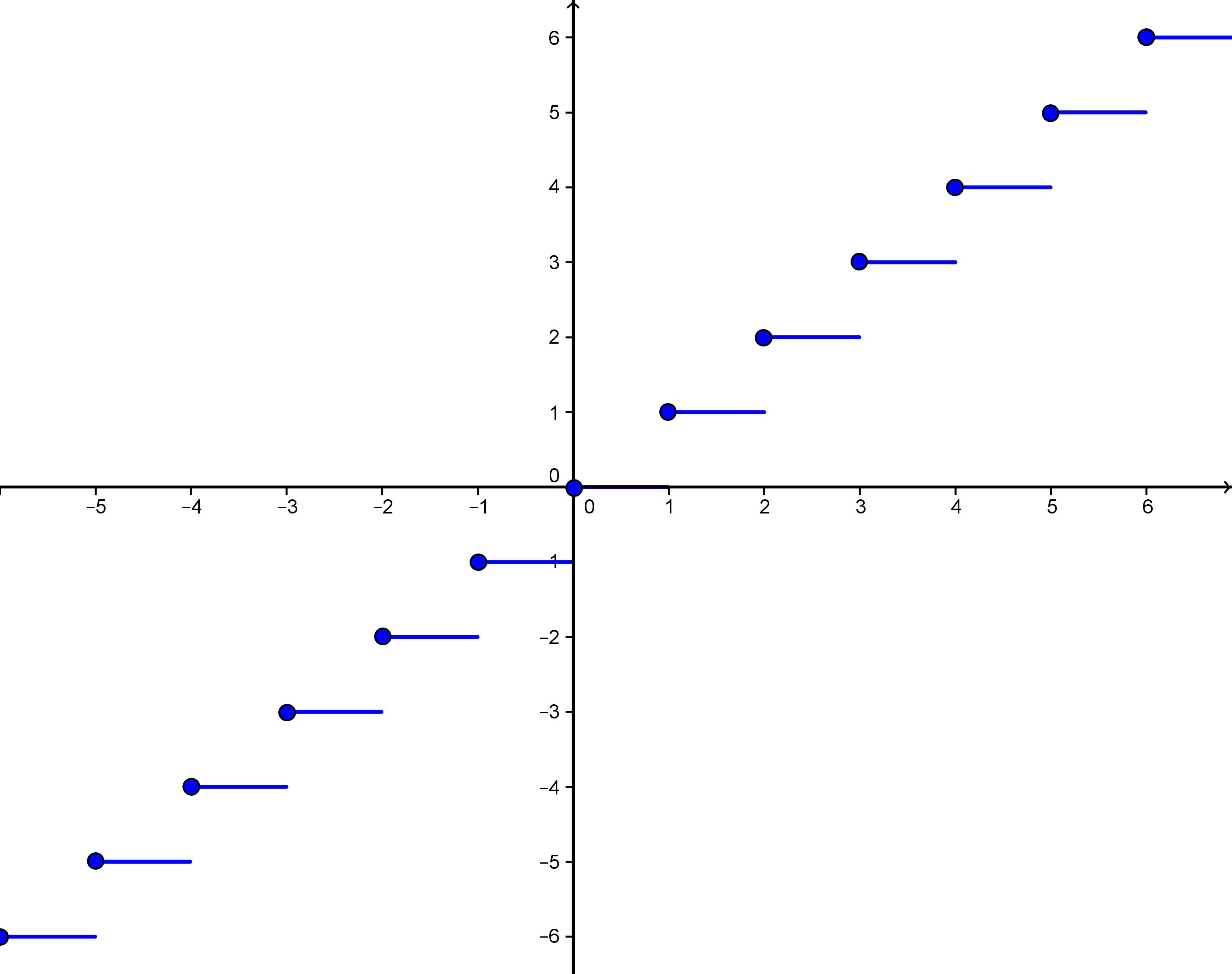
Graph of the

floor

function

Let a real number

a \geq 0

be given, written as a decimal number

a = g_{n} g_{n - 1} \dots g_{1} g_{0} . a_{1} a_{2} a_{3} \dots

This number

a

can be rounded to

r

fractional digits (

r \in ℕ_{0}

) using the

floor

function by

\tilde{a} = \frac{1}{10^{r}} \cdot ⌊ 10^{r} \cdot a ⌋ .

This process of rounding cuts off the decimal after the

r

th fractional digit. Thus, rounding using the

floor

function is in general a rounding off.

Example 11.1.4

Rounding the number

a_{1} = 2.3727

to 2 fractional digits using the

floor

function results in

{\tilde{a}}_{1} = \frac{1}{10^{2}} \cdot ⌊ 10^{2} \cdot 2.3727 ⌋ = \frac{1}{10^{2}} \cdot ⌊ 237.27 ⌋ = \frac{1}{10^{2}} \cdot 237 = = 2.37 .

Alternatively, it can be rounded by cutting off the decimal after the second fractional digit (however, this is only possible if the number is given as a decimal which is rarely the case in a computer program).
Rounding the number

a_{2} = \sqrt{2} = 1.414213562 \dots

to 4 fractional digits using the

floor

function results in

{\tilde{a}}_{2} = \frac{1}{10^{4}} \cdot ⌊ 10^{4} \cdot \sqrt{2} ⌋ = \frac{1}{10^{4}} \cdot ⌊ 14142.1 \dots ⌋ = \frac{1}{10^{4}} \cdot 14142 = 1.4142 .

Rounding the number

a_{3} = π = 3,141592654 \dots

to 2 fractional digits using the

floor

function results in

{\tilde{a}}_{3} = \frac{1}{10^{2}} \cdot ⌊ 10^{2} \cdot π ⌋ = \frac{1}{10^{2}} \cdot ⌊ 314.159 \dots ⌋ = \frac{1}{10^{2}} \cdot 314 = 3.14 .

The rounding method using the

floor

function is often applied for calculating final grades in certificates ("academic rounding"). If a mathematics student has the individual grades

Subject	Grade
Mathematics 1	$1.3$
Mathematics 2	$2.3$
Mathematics 3	$2.0$

then the arithmetic mean of these grades is calculated by

\frac{1.3 + 2.3 + 2.0}{3} = \frac{5.6}{3} = 1.8 \overline{6} .

Rounding to the first fractional digit using the

floor

function would result in the final grade of

\tilde{a} = 1.8

. The rounding methods for calculating final grades always have to be described exactly in the examination regulations.
The counterpart to the

floor

function is the

ceil

(a.k.a. ceiling) function:

Info 11.1.5

The $ceil$ function is defined as

ceil : ℝ \to ℝ, x ⟼ ceil (x) = ⌈ x ⌉ = min {k \in ℤ : k \geq x} .

x \in ℝ

is a real number, then

ceil (x) = ⌈ x ⌉

is the smallest integer that is greater than or equal to

x

. The

ceil

function is a step function with jumps (jump discontinuities) of height

1

at all points

x \in ℤ

. The function values at the jumps always lie at the bottom. They are indicated by the small circles in the figure below showing the graph of the

ceil

function.

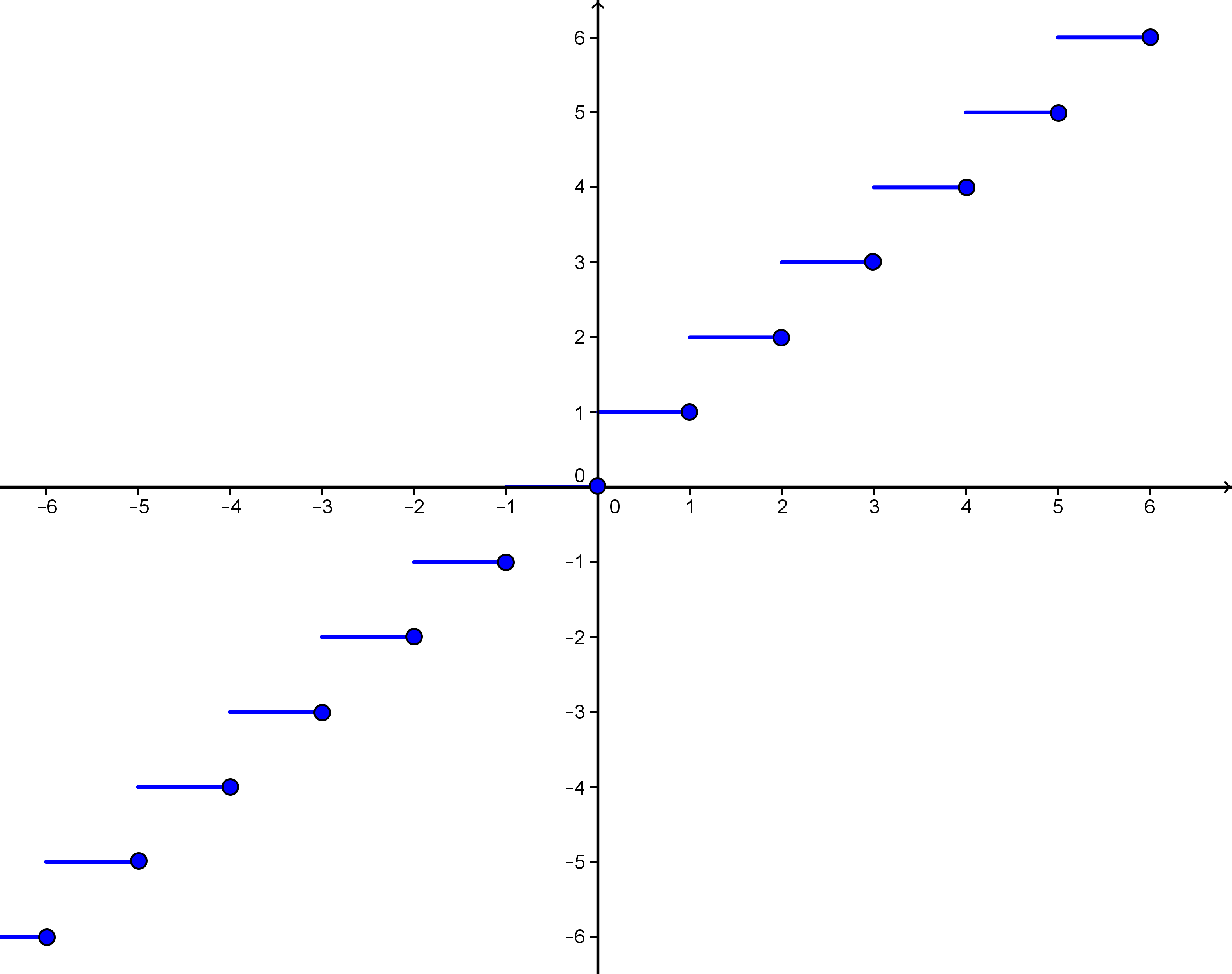
Graph of the

ceil

function

Let a real number

a \geq 0

be given as a decimal number

a = g_{n} g_{n - 1} \dots g_{1} g_{0} . a_{1} a_{2} a_{3} \dots

This number

a

can be rounded to

r

fractional digits (

r \in ℕ_{0}

) using the

ceil

function by

\hat{a} = \frac{1}{10^{r}} \cdot ⌈ 10^{r} \cdot a ⌉ .

Rounding using the

ceil

function is in general a rounding up to the next decimal digit.

Example 11.1.6

Rounding the number

a_{1} = 2.3727

2

fractional digits using the

ceil

function results in

{\hat{a}}_{1} = \frac{1}{10^{2}} \cdot ⌈ 10^{2} \cdot 2.3727 ⌉ = \frac{1}{10^{2}} \cdot ⌈ 237.27 ⌉ = \frac{1}{10^{2}} \cdot 238 = 2.38 .

Analogously, rounding the number

a_{2} = \sqrt{2} = 1.414213562 \dots

4

fractional digits using the

ceil

function results in

{\hat{a}}_{2} = \frac{1}{10^{4}} \cdot ⌈ 10^{4} \cdot \sqrt{2} ⌉ = \frac{1}{10^{4}} \cdot ⌈ 14142.1 \dots ⌉ = \frac{1}{10^{4}} \cdot 14143 = 1.4143 .

Rounding the number

a_{3} = π = 3.141592654 \dots

2

fractional digits using the

ceil

function results in

{\hat{a}}_{3} = \frac{1}{10^{2}} \cdot ⌈ 10^{2} \cdot π ⌉ = \frac{1}{10^{2}} \cdot ⌈ 314.15 \dots ⌉ = \frac{1}{10^{2}} \cdot 315 = 3.15 .

The rounding method using the

ceil

function is often applied, for example, in craftsmen's invoices. A craftsman is mostly paid by the hour. If a repair takes 50 minutes (i.e.

0.8 \overline{3}

hours as a decimal), then a craftsmen will round up and invoice a full working hour. Colloquially, rounding mostly means mathematical rounding:

Info 11.1.7

The $round$ function (or mathematical rounding) is defined as

round : ℝ \to ℝ, x ⟼ round (x) = floor (x + \frac{1}{2}) = ⌊ x + \frac{1}{2} ⌋ .

In contrast to rounding up or rounding off, the maximum change to the number by this rounding is

0.5

The

round

function is a step function with jumps (jump discontinuities) of height

1

at all points

x + \frac{1}{2}, x \in ℤ

. The function values at the jumps always lie a step up. They are indicated by the small circles in the figure below showing the graph of the

round

function.

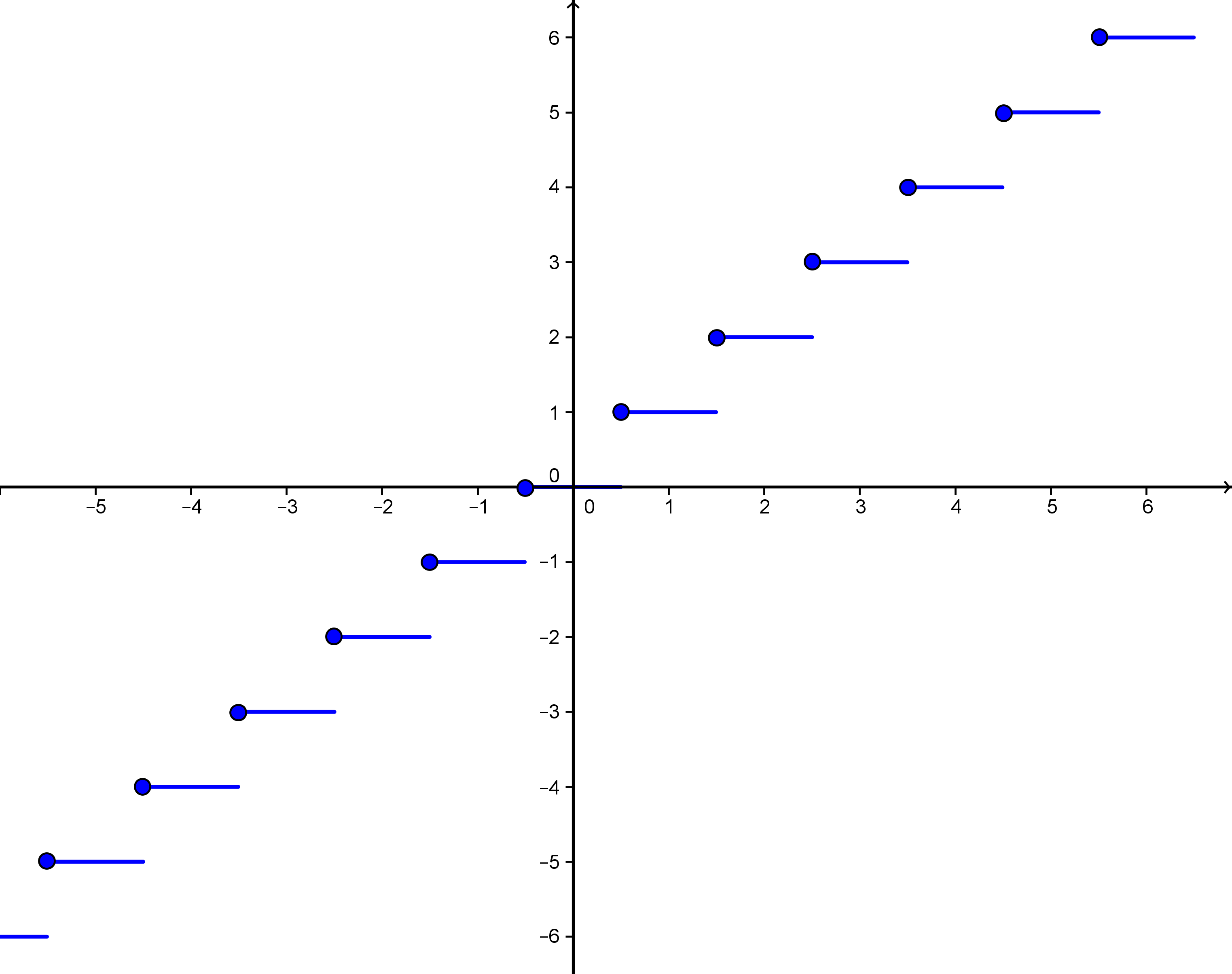
Graph of the

round

function

Let a real number

a \geq 0

be given as a decimal number

a = g_{n} g_{n - 1} \dots g_{1} g_{0} . a_{1} a_{2} a_{3} \dots

This number

a

can be rounded to

r

fractional digits (

r \in ℕ_{0}

) using the

round

function:

\overline{a} = \frac{1}{10^{r}} \cdot round (10^{r} \cdot a) = \frac{1}{10^{r}} \cdot ⌊ 10^{r} \cdot a + \frac{1}{2} ⌋ .

This rounding method is called mathematical rounding and corresponds to the "normal" rounding process.

Example 11.1.8

The number

a_{1} = 1.49

is rounded to one fractional digit using the

round

function to

\begin{matrix} {\overline{a}}_{1} & = & \frac{1}{10} \cdot round (10 \cdot 1.49) = \frac{1}{10} \cdot ⌊ 10 \cdot 1.49 + 0.5 ⌋ \\ = & \frac{1}{10} \cdot ⌊ 14.9 + 0.5 ⌋ = \frac{1}{10} \cdot ⌊ 15.4 ⌋ = \frac{1}{10} \cdot 15 = 1.5 . \end{matrix}

The number

a_{2} = 1.52

is rounded to one fractional digit using the

round

function to

\begin{matrix} {\overline{a}}_{2} & = & \frac{1}{10} \cdot round (10 \cdot 1.52) = \frac{1}{10} \cdot ⌊ 10 \cdot 1.52 + 0.5 ⌋ \\ = & \frac{1}{10} \cdot ⌊ 15.2 + 0.5 ⌋ = \frac{1}{10} \cdot ⌊ 15.7 ⌋ = \frac{1}{10} \cdot 15 = 1.5 . \end{matrix}

The number

a_{3} = 2.3727

is rounded to two fractional digits using the

round

function to

\begin{matrix} {\overline{a}}_{3} & = & \frac{1}{10^{2}} \cdot round (10^{2} \cdot 2.3727) = \frac{1}{100} \cdot ⌊ 100 \cdot 2.3727 + 0.5 ⌋ \\ = & \frac{1}{100} \cdot ⌊ 237.27 + 0.5 ⌋ = \frac{1}{100} \cdot ⌊ 237.77 ⌋ = \frac{1}{100} \cdot 237 = 2.37 . \end{matrix}

The number

a_{4} = \sqrt{2} = 1.414213562 \dots

is rounded to seven fractional digits using the

round

function to

\begin{matrix} {\overline{a}}_{3} & = & \frac{1}{10^{7}} \cdot round (10^{7} \cdot \sqrt{2}) = \frac{1}{10^{7}} \cdot ⌊ 10^{7} \cdot 1.414213562 \dots + 0.5 ⌋ \\ = & \frac{1}{10^{7}} \cdot ⌊ 14142135.62 \dots + 0.5 ⌋ = \frac{1}{10^{7}} \cdot ⌊ 14142136.12 \dots ⌋ \\ = & \frac{1}{10^{7}} \cdot 14142136 = 1.4142136 . \end{matrix}

Exercise 11.1.9

Using the

round

function, round the number

π = 3.141592654 \dots

to four fractional digits:

\overline{π}

=

\begin{matrix} \overline{π} & = & \frac{1}{10^{4}} \cdot round (10^{4} \cdot π) = \frac{1}{10^{4}} \cdot ⌊ 10^{4} \cdot 3.141592654 \dots + 0.5 ⌋ \\ = & \frac{1}{10^{4}} \cdot ⌊ 31415.92654 \dots + 0.5 ⌋ = \frac{1}{10^{4}} \cdot ⌊ 31416.42654 \dots ⌋ \\ = & \frac{1}{10^{4}} \cdot 31416 = 3.1416 . \end{matrix}

Exercise 11.1.10

Let the numbers

a = \frac{47}{17} and b = 3.7861

be given.

Round each of the numbers $a$ and $b$ to $2$ fractional digits using the $floor$ function.
The roundings result in $\tilde{a}$ $=$
and $\tilde{b}$ $=$ .
Round each of the numbers $a$ and $b$ to $2$ fractional digits using the $ceil$ function.
The roundings result in $\hat{a}$ $=$
and $\hat{b}$ $=$ .
Round each of the numbers $a$ and $b$ to $2$ fractional digits using the $round$ function.
The roundings result in $\overline{a}$ $=$
and $\overline{b}$ $=$ .

First, we transform the fraction into an appropriate decimal fraction by dividing successively with remainder and substituting the results of the division as digits into the decimal:

\frac{47}{17} = 2 + \frac{13}{17} .

The digit left to the decimal point is

2

. We have

2 + \frac{13}{17} = 2 + \frac{1}{10} \cdot \frac{130}{17} = 2 + \frac{1}{10} \cdot (7 + \frac{11}{17}) .

The first fractional digit is

7

. Proceeding further this way results in

a = 2.764705 \dots

, we only need three fractional digits for the required rounding. The complete calculation using the

floor

function results in

\tilde{a} = \frac{1}{10^{2}} \cdot ⌊ 10^{2} \cdot 2.764705 \dots ⌋ = \frac{1}{10^{2}} \cdot ⌊ 276.4705 \dots ⌋ = 2.76 .

This result can be obtained more quickly by simply cutting off the decimal after the second decimal digit:

\tilde{a} = 2.76 and \tilde{b} = 3.78 .

However, this is only allowed in this exercise since

a

and

b

are non-negative. A simple rounding up after the second decimal digit or a complete calculation using the

ceil

function results in

\hat{a} = 2.77 and \hat{b} = 3.79 .

The results for the mathematical rounding are obtained either by a complete calculation as in the examples above, or by rounding to the decimal with two fractional digits with the smallest difference from the original number:

\overline{a} = 2.76 and \overline{b} = 3.79 .

Onlinebrückenkurs Mathematik

1. Elementary Arithmetic

2. Equations in one Variable

3. Inequalities in one Variable

4. System of Linear Equations

5. Geometry

6. Elementary Functions

7. Differential Calculus

8. Integral Calculus

9. Objects in the Two-Dimensional Coordinate System

10. Basic Concepts of Descriptive Vector Geometry

11. Language of Descriptive Statistics

Chapter 11 Language of Descriptive Statistics

11.1.2 Rounding

Info 11.1.3

Example 11.1.4

Info 11.1.5

Example 11.1.6

Info 11.1.7

Example 11.1.8

Exercise 11.1.9

Exercise 11.1.10