Chapter 11 Language of Descriptive Statistics
Section 11.2 Frequency Distributions and Percentage Calculation11.2.4 Continuous Compounding Interest
The expression with can also be interpreted as a map depending on
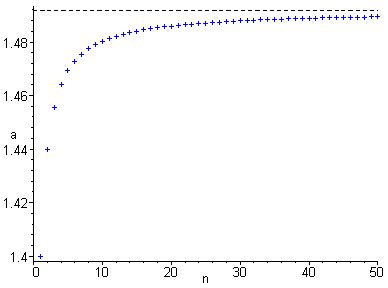
A map is called a real sequence. The pairs can be interpreted as points in the Euclidean plane. In this sense, the sequence is shown in the figure below as a sequence of points in the Euclidean plane.
Two properties of this sequence can immediately be seen from the figure above:
- The sequence , is monotonically increasing, i.e. for , for all .
- The sequence approaches the value as increases. This number is called limit of the sequence , and is written
will be studied in detail.
There, the following statement will be shown:
Info 11.2.17
For an arbitrary number , we have
For , the limit of this sequence is Euler's number (named after the Swiss mathematician Leonhard Euler, 1707-1783):
It can be shown (with some difficulty) that Euler's number is an irrational number, and hence it cannot be written as a fraction.
The exponent rules apply to the natural exponential function with arbitrary real numbers as its exponents:
- for .
- for .
Information on the compound interest process can be gained if the number of times gets very large using the exponential function and the relation to the sequence : the capital is multiplied by a factor of every year if the interest at a rate of is credited to the initial capital at different times in the year. After years, , the initial capital has increased to
If , the limit of this sequence is
For increasing the interest is paid more and more frequently:
Example 11.2.19
An investment of EUR is deposited for years in a bank account where continuous compounding interest is applied at a yearly interest rate of . After years, this results in an investment of
 Onlinebrückenkurs Mathematik
Onlinebrückenkurs Mathematik