Chapter 11 Language of Descriptive Statistics

Section 11.4 Final Test

11.4.1 Final Test Module 11

This is a test for submission:
  • Unlike open exercises, no hints for formulating mathematical expressions are provided.
  • The test can be restarted or interrupted at any time.
  • The test can be terminated and submitted using the buttons at the end of the page, or reset.
  • The test can be attempted several times. Only the last version will be included in the statistics.


Exercise 11.4.1
For bonds (e.g. government bonds),we distinguish between the nominal value and the issue price (quote). Bonds can be issued at nominal value, under nominal value or over nominal value. The issue price is closer to the nominal value the more the bond interest corresponds to the current market rate. A customer buys bonds with a nominal value of K=10,000 EUR, an issue price of 100%, an interest rate of p=4,5% p. a., and a period of t=10 years.
  1. How much interest is paid at the end of each interest period for an issue price of 100% when simple interest is applied. Answer: the annually paid interest is
    EUR.
  2. Specify the amount of the totally paid capital at the end of the period if simple interest is applied. Answer: the amount of capital paid at the end of the period is
    EUR.

Exercise 11.4.2
A capital of K=25,000 EUR will be invested with an annually paid interest rate of p=3,5% p. a. until the amount of the capital has doubled. How many years does the capital have to be invested, if continuous compounding interest is applied?  
Answer: the required investment period is t  = 
years.  
Round up your result to the text integer.

Exercise 11.4.3
Read off the properties of the described sample from the histogram shown in the figure below.
 
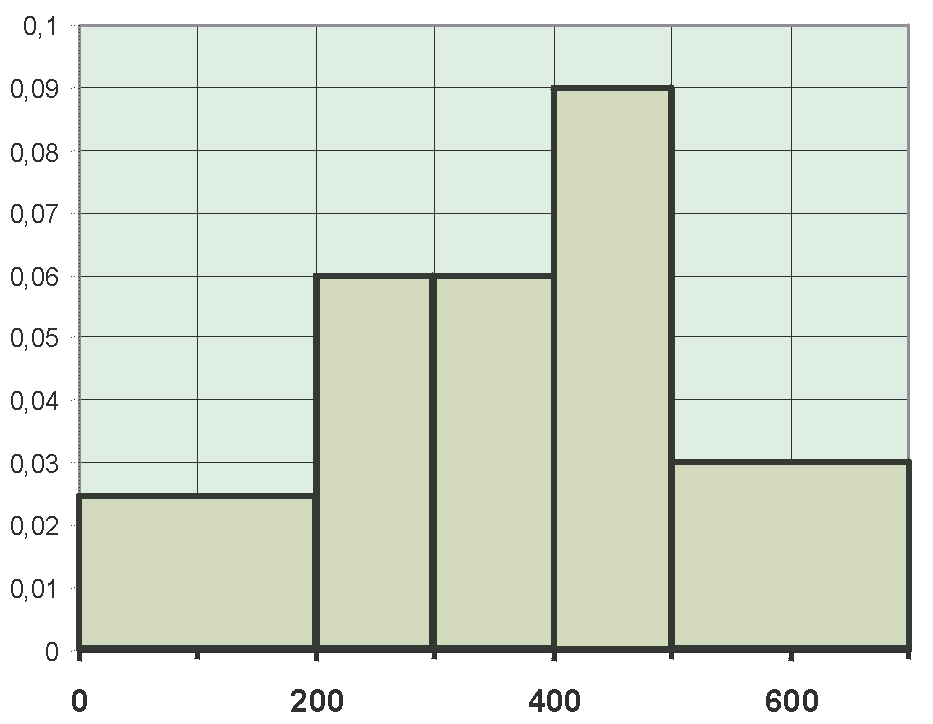
Histogram of the sample x=( x1 ,…, xn ).

Specify the interval boundaries of the five classes and the corresponding relative frequencies. Fill in the frequency table. For this purpose, calculate the ratios of the areas of the single bars in the diagram to the total area.
Class Interval rel. Class frequencies hj
Class 1 [0;200) 0,16
Class 2

Class 3

Class 4

Class 5


Exercise 11.4.4
The measurement of the weight of n=11 watermelons (in kilogram) resulted in the following values:
Number j 1 2 3 4 5 6 7 8 9 10 11
Weight xj in kilogram 6.2 5.5 7.3 6.8 6.3 5.5 4.5 6.5 7.3 5.7 5.6

  1. Find the arithmetic mean of the 11 sample values: x ‾  =  .
  2. Find the median of the 11 sample values: x ~  =  .

Enter your result rounded to two fractional digits. Do not use a calculator but try to find the values by hand.

 
        

The test evaluation will be displayed here!


: