Chapter 2 Equations in one Variable

Section 2.1 Simple Equations

2.1.5 Solving quadratic Equations

Info 2.1.20
 
A quadratic equation is an equation of the form a x2 +bx+c=0 with a≠0, or, in reduced form, x2 +px+q=0. This form is obtained by dividing the equation by a.
For a quadratic equation in one variable (here the variable x) one of the following three statements holds:
  • The quadratic equation has no solution: L={}.
  • The quadratic equation has a single solution L={ x1 }.
  • The quadratic equation has two different solutions L={ x1 ; x2 }.

The solutions are obtained by applying quadratic solution formulas.
Info 2.1.21
 
The pq formula for solving the equation x2 +px+q=0 reads

x1,2   =  - p 2 ± 1 4 p2 -q .

Here, the equation has
  • no (real) solution if 1 4 p2 -q<0 (taking the square root is not allowed),
  • a single solution x1 =- p 2 if 1 4 p2 =q and the square root is zero,
  • two different solutions if the square root is a positive number.

The expression D:= 1 4 p2 -q underneath the square root considered above is called the discriminant.
The solution of a quadratic equation is often described by an alternative formula:
Info 2.1.22
 
For the equation a x2 +bx+c=0 with a≠0 the abc formula reads

x1,2   =   -b± b2 -4ac 2a  .

Here, the equation has
  • no (real) solution if b2 -4ac<0 (the square root of a negative number is undefined within the range of real numbers),
  • a single solution x1 =- b 2a if b2 =4ac and the square root is zero,
  • two different solutions if the square root is a positive number.
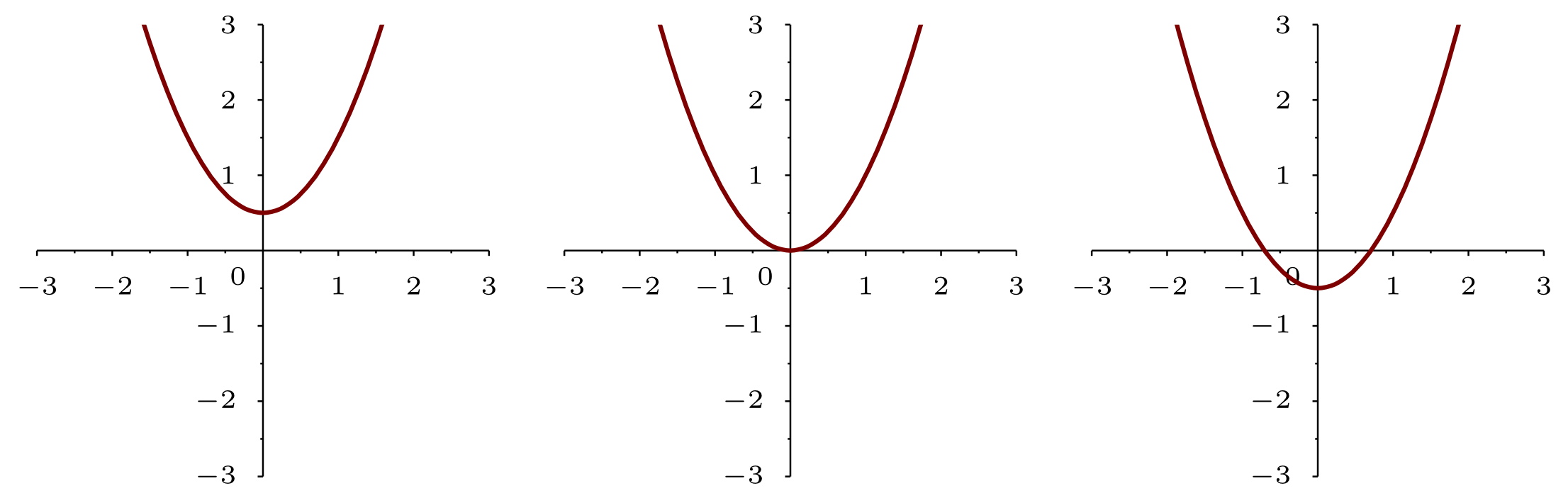
Again, the expression D:= b2 -4ac underneath the square root considered above is called the discriminant.
Both formulas result in the same solutions. The pq formula is easier to learn, but is only applicable if a, the coefficient of the quadratic term, is  1. Otherwise we must divide both sides of the equation by  a.

In terms of the pq formula, the three different cases correspond to three possibilies for the number of intersection points that the graph of a shifted standard parabola f(x)= x2 +px+q may have with the x axis.

Three cases: no intersection point, one intersection point, two intersection points with the x axis.
Example 2.1.23
The quadratic equation x2 -x+1=0 has no solution since the discriminant 1 4 p2 -q=- 3 4 within the pq formula is negative. In contrast, the equation x2 -x-1=0 has two solutions

x1 = 1 2 + 1 4 +1  =   1 2 (1+5) ,  x2 = 1 2 - 1 4 +1  =   1 2 (1-5) .


Info 2.1.24
 
The function expression of a parabola has vertex form if the function has the form f(x)=a·(x-s )2 -d with a≠0. In this case, (s;-d) is the vertex of the parabola. The corresponding quadratic equation for f(x)=0 then reads a·(x-s )2 =d.
Dividing this equation by a one obtains the equivalent quadratic equation (x-s )2 = d a . Since the left-hand side is a square of a real number, only solutions exist if and only if the right-hand side is non-negative as well, i.e. d a ≥0. By taking the square root, taking the two possible signs into account, one obtains x-s=± d a .
So, for d a >0 two solutions of the equation exist:

x1   =  s- d a  ,   x2   =  s+ d a  ;

they are symmetric to the x coordinate s of the vertex. For d=0, only one solution exists.
The sign of a determines whether the function expression describes a parabola opening upwards or downwards.

The quadratic equation has only one single solution s if it can be transformed into the form (x-s )2 =0.
Info 2.1.25
 

Any quadratic equation can be transformed (after collecting terms on the left-hand side and normalisation, if necessary) to vertex form by completing the square. For this, a constant is added to both sides of the equation such that on the left-hand side we have a term of the form x2 ±2sx+ s2 to which the first or second binomial formula can be applied.

Example 2.1.26
Adding the constant 2 transforms the equation x2 -4x+2=0 into the form x2 -4x+4=2 or into the form (x-2 )2 =2, respectively. From this, the two solutions x1 =2-2 and 2+2 can be seen immediately. In contrast, the quadratic equation x2 +x=-2 has no solution since completing the square results in x2 +x+ 1 4 =- 7 4 or (x+ 1 2 )2 =- 7 4 , respectively, where the right-hand side is negative for a=1.

Exercise 2.1.27
Find the solutions of the following quadratic equations by completing the square after collecting terms on the left-hand side and normalisation (i.e. selecting a=1):
  1. x2 =8x-1 has the vertex form
     =  .
    The solution set is L  =  .
  2. x2 =2x+2+2 x2 has the vertex form
     =  .
    The solution set is L  =  .
  3. x2 -6x+18=- x2 +6x has the vertex form
     =  .
    The solution set is L  =  .
Enter sets in the form { a;b;c; …}. Enter the empty set as {}.



: