Chapter 2 Equations in one Variable

Section 2.2 Absolute Value Equations

2.2.3 Mixed Equations

Info 2.2.19

If an equation contains both absolute values and other expressions, the case analysis has to be done according to the absolute value terms and applied only to these.

Finally, keep in mind to cross-check the solution sets you found with the case conditions.

Example 2.2.20

Solve the equation

| x - 1 | + x^{2} = 1

. Here, the case analysis is as follows:

For $x \geq 1$ , the absolute value bars can be replaced by normal brackets which results in the quadratic equation $(x - 1) + x^{2} = 1$ that is transformed into the equation $x^{2} + x - 2 = 0$ . Using the $p q$ formula we get the two solutions

$\begin{matrix} x_{1} & = & - \frac{1}{2} - \sqrt{\frac{9}{4}} = - 2, \\ x_{2} & = & - \frac{1}{2} + \sqrt{\frac{9}{4}} = 1 \end{matrix}$
of which only $x_{2}$ satisfies the case condition.
For $x < 1$ , one obtains the quadratic equation $- (x - 1) + x^{2} = 1$ that is transformed into the equation $x^{2} - x = 0$ or $x \cdot (x - 1) = 0$ , respectively. The product representation indicates the two solutions $x_{3} = 0$ and $x_{4} = 1$ . Because of the case condition only $x_{3} = 0$ is a solution of the initial equation.

So, altogether

L = {0; 1}

is the solution set of the initial equation.

Exercise 2.2.21

Find the solution set of the mixed equation

| x - 3 | \cdot x = 9

If $x$ is in the interval
the absolute value term is non-negative.
One obtains the quadratic equation
$=$ $0$ .
The solution set is .
Only the solution
satisfies the case condition.
If $x$ is in the interval
the absolute value term is negative.
One obtains the normalised quadratic equation
$=$ $0$ .
The solution set is .

Enter open intervals in the form

(3; 5)

and closed intervals in the form

[3; 5]

. Enter "infinity" as text or simply as infty. Do not use the notation

] a; b [

fir open intervals. Sets can be entered by listing the elements in the form

{1; 2; 3}

. For the set brackets enter AltGr+7 or AltGr+0, respectively.
So, altogether the solution set is

L

=

x

is in the interval

[3; \infty [

the absolute value term is non-negative and one obtains the quadratic equation

x^{2} - 3 x - 9 = 0

with the solution set

L = {\frac{3}{2} - \sqrt{\frac{45}{4}}; \frac{3}{2} + \sqrt{\frac{45}{4}}}

. Only the larger solution

\frac{3}{2} + \sqrt{\frac{45}{4}}

satisfies the condition

x \geq 3

. This can also be seen without any calculator by estimating

\sqrt{\frac{45}{4}} \geq \sqrt{\frac{36}{4}} = 3

. In contrast, if

x

is in the interval

] - \infty; 3 [

the absolute value term is negative. One obtains the normalised quadratic equation

x^{2} - 3 x + 9 = 0

. Because of

\frac{1}{4} p^{2} - q < 0

in the

pq

formula this equation is unsolvable. Hence, the initial equation has only one solution

\frac{3}{2} + \sqrt{\frac{45}{4}}

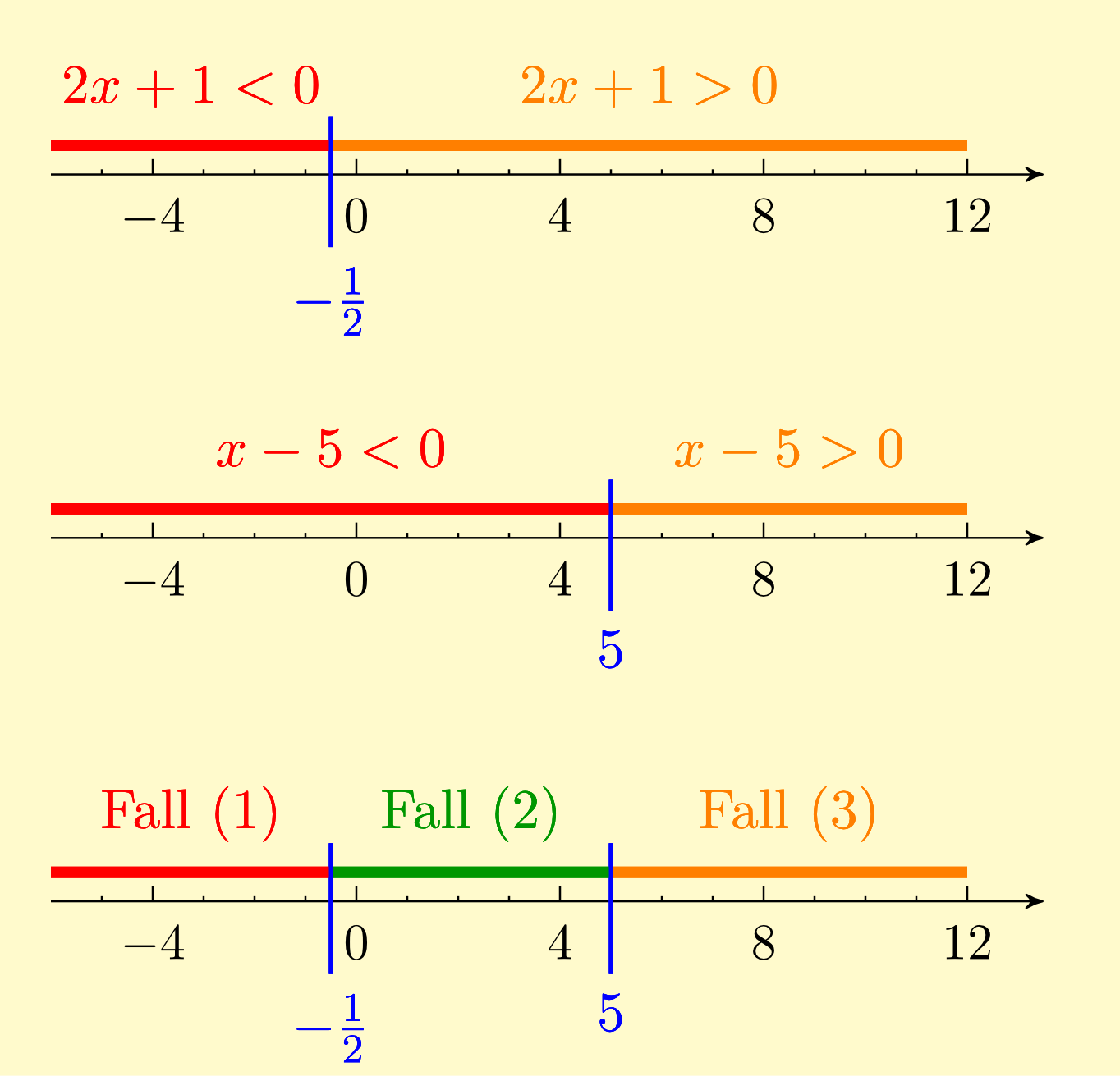
Exercise 2.2.22

Find the solutions of the mixed absolute value equation

3 | 2 x + 1 | = | x - 5 |

by visualising the different cases on the number line and finally solving the equation by case analysis. First, visualise the case analysis for each absolute value.
The solution set is .

Visualising the different cases for the expressions

| 2 x + 1 |

and

| x - 5 |

above each other indicates all cases to be distinguished:

Illustration of the three cases

According to the figure above the following three cases have to be distinguished:

Case (1): For $x < - \frac{1}{2}$ both terms in the absolute value terms are negative.
Case (2): For $- \frac{1}{2} \leq x < 5$ the term in the second absolute value term is negative but the term in the first one is not.
Case (3): For $5 \leq x$ both terms in the absolute value terms are non-negative.
Obviously, there is no $x$ for which the first term is negative and the second term is non-negative.

So, the solutions can be summarised:

In case (1), both absolute values reverse the sign of the terms:
$3 | 2 x + 1 | = | x - 5 | \Leftrightarrow 3 (- (2 x + 1)) = - (x - 5)$ .
This equation has the solution $x = - \frac{8}{5}$ satisfying the case condition.
In case (2), only the second absolute value reverses the sign of the term:
$3 | 2 x + 1 | = | x - 5 | \Leftrightarrow 3 (2 x + 1) = - (x - 5)$ .
This equation has the solution $x = \frac{2}{7}$ satisfying the case condition.
In case (3), the absolute value bars in both terms can be omitted (replaced by normal brackets):
$3 | 2 x + 1 | = | x - 5 | \Leftrightarrow 3 (2 x + 1) = (x - 5)$ .
This equation has the solution $x = - \frac{8}{5}$ , but this solution does not satisfy the case condition. Thus, it will be discarded within its case analysis.

Therefore, the solution set is

{- \frac{8}{5}; \frac{2}{7}}

Onlinebrückenkurs Mathematik

1. Elementary Arithmetic

2. Equations in one Variable

3. Inequalities in one Variable

4. System of Linear Equations

5. Geometry

6. Elementary Functions

7. Differential Calculus

8. Integral Calculus

9. Objects in the Two-Dimensional Coordinate System

10. Basic Concepts of Descriptive Vector Geometry

11. Language of Descriptive Statistics