2.2.1 Introduction

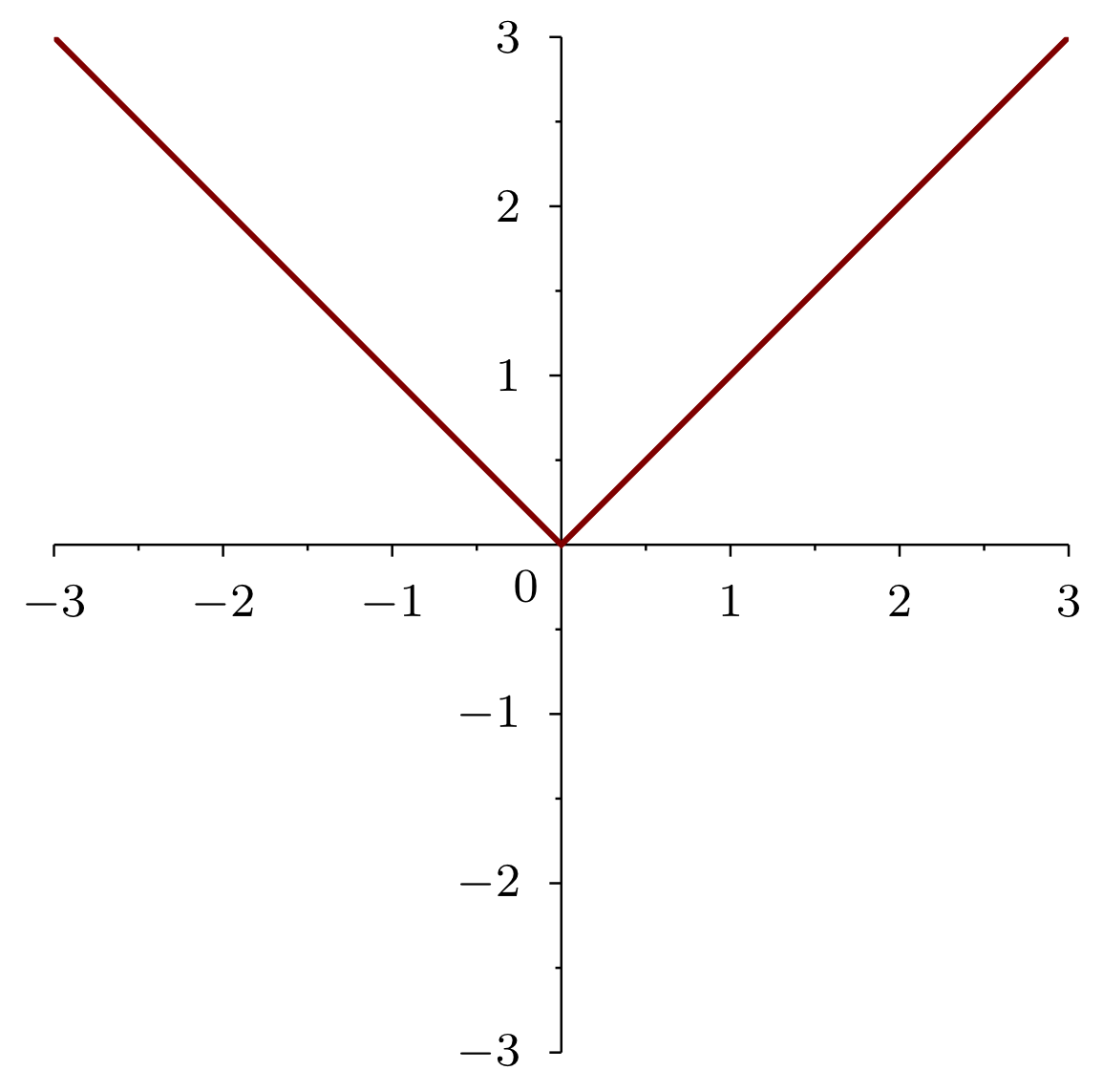
The absolute value $|x|$ assigns a variable $x\in ℝ$ its value without sign: If $x\ge 0$, then $|x|=x$, otherwise $|x|=-x$ (see figure).

Absolute value equations are equations in which one absolute value or several absolute values occur. Problems arise since the absolute value is calculated by distinguishing the two cases

${\displaystyle \left|\hspace{0.5em}\text{term}\hspace{0.5em}\right|\mathrm{\hspace{0.5em}\hspace{0.5em}}\mathrm{\hspace{0.5em}\hspace{0.5em}}=\mathrm{\hspace{0.5em}\hspace{0.5em}}\mathrm{\hspace{0.5em}\hspace{0.5em}}\{\begin{array}{cc}\hfill \text{term}& \text{for}\mathrm{\hspace{0.5em}\hspace{0.5em}}\text{term}\ge 0\hfill \\ \hfill -\text{term}& \text{for}\mathrm{\hspace{0.5em}\hspace{0.5em}}\text{Term}<0\hfill \end{array}\hspace{0.5em}.}$

For solving absolute value equations, these cases have to be solved step by step and analysed to find the solutions.

As soon as beside the absolute value several other terms occur a case analysis is required. In the following section we will explain in detail how this analysis is done and how it is written correctly since the case analysis will play an important role in the next modules.