Kapitel 6 Elementare Funktionen

Abschnitt 6.1 Grundlegendes zu Funktionen

6.1.2 Zuordnungen zwischen Mengen

Wir beginnen mit einem ersten Beispiel einer Funktion als Zuordnung zwischen zwei Mengen. Dazu betrachten wir die Menge der natürlichen Zahlen $\mathbb{N}$ sowie die Menge der rationalen Zahlen $\mathbb{Q}$ und veranschaulichen uns diese als zwei ,,Container" mit Zahlen.

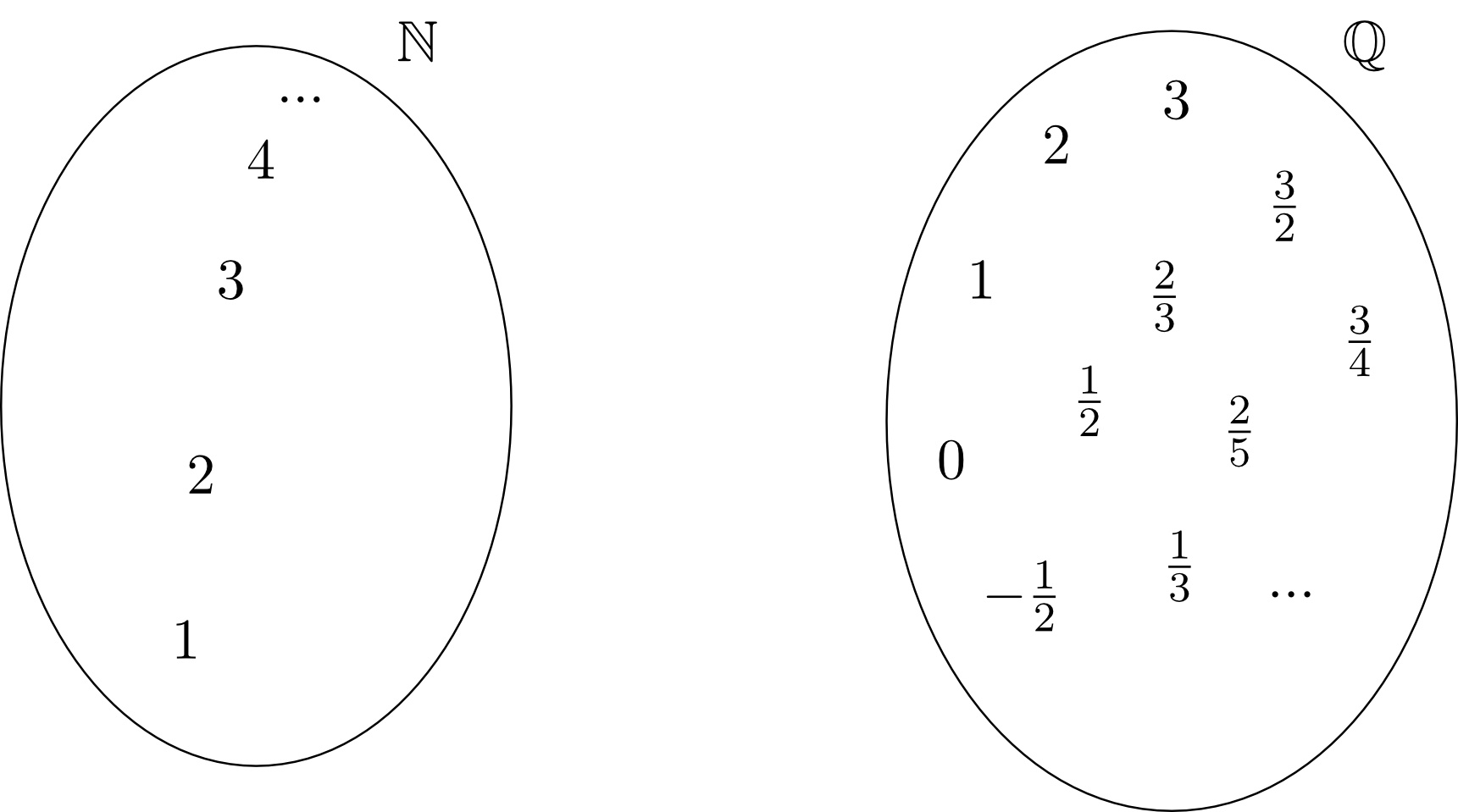
Nun wollen wir eine Zuordnung zwischen den Elementen dieser beiden Mengen auf folgende Art durchführen. Jeder beliebigen Zahl $n\in \mathbb{N}$ wird die Hälfte dieser Zahl $\frac{n}{2}\in \mathbb{Q}$ zugeordnet, also der Zahl $1\in \mathbb{N}$ die Zahl $\frac{1}{2}\in \mathbb{Q}$, der Zahl $2\in \mathbb{N}$ die Zahl $1\in \mathbb{Q}$ und immer so weiter. Dies können wir im Bild durch Pfeile veranschaulichen, die andeuten, welche Zahlen in $\mathbb{N}$ welchen Zahlen in $\mathbb{Q}$ zugeordnet werden.

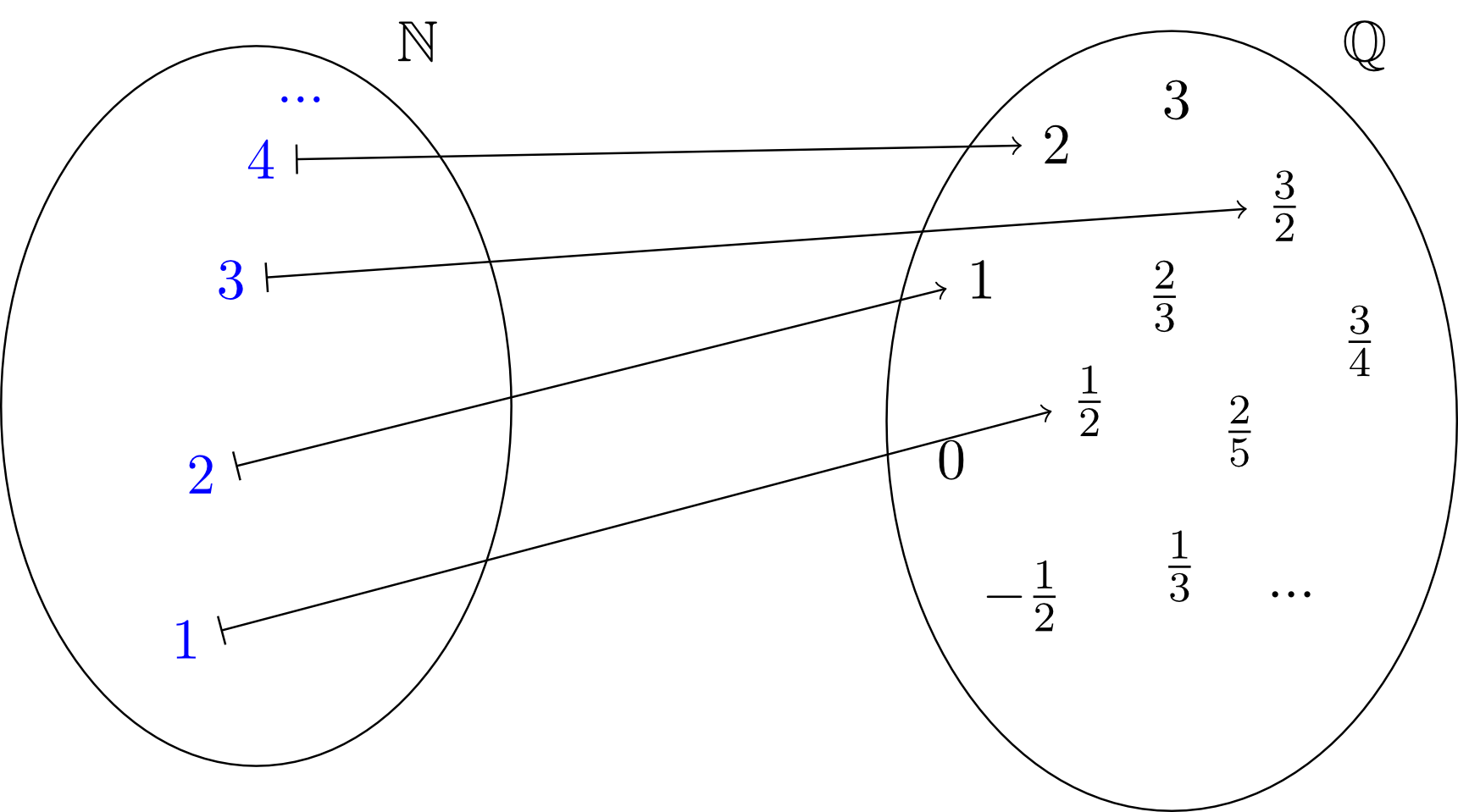
Wir benutzen für die Zuordnung der einzelnen Elemente der Mengen, die wir oben in Worten beschrieben haben, den sogenannten Zuordnungspfeil. Dies ist ein Pfeil, der auf einer Seite einen senkrechten Strich als Abschluss hat: $⟼$. Er bedeutet, dass der Zahl auf der Seite mit dem senkrechten Strich die Zahl auf der Seite der Pfeilspitze zugeordnet wird:

${\displaystyle \mathbb{N}\ni 1⟼0.5\in \mathbb{Q}\hspace{0.5em},\hspace{0.5em}\hspace{0.5em}\mathbb{N}\ni 2⟼1\in \mathbb{Q}\hspace{0.5em},\hspace{0.5em}\hspace{0.5em}\text{usw.}}$
Mit diesen Zuordnungen haben wir nun eine Funktion von den natürlichen Zahlen $\mathbb{N}$ in die rationalen Zahlen $\mathbb{Q}$ konstruiert. In der Mathematik gibt man dieser Zuordnung nun einen Namen, d.h. man reserviert ein Symbol (oft $f$ für Funktion), das genau diese Zuordnung beschreiben soll. Dazu muss man die Zahlenmengen notieren, aus denen und in die zugeordnet werden soll. In diesem Fall werden den Elementen der natürlichen Zahlen $\mathbb{N}$ rationale Zahlen zugeordnet. Dies schreibt man mathematisch mit einem sogenannten Abbildungspfeil $\to$, an dessen Spitze die Menge auftaucht, die das Ziel der Zuordnung ist und an dessen Basis die Menge steht, deren Elemente zugeordnet werden. In diesem Fall also

${\displaystyle f:\mathbb{N}\to \mathbb{Q}\hspace{0.5em}.}$
Man liest dies als ,,die Funktion $f$ bildet von $\mathbb{N}$ nach $\mathbb{Q}$ ab".
Weiterhin können wir uns nun die Frage stellen, ob wir die Zuordnungen dieser Funktion $1⟼\frac{1}{2},\hspace{0.5em}2⟼1,\hspace{0.5em}\text{usw.}$ kürzer aufschreiben können. Dazu erinnern wir uns an den Beginn dieses Beispiels. Wir haben uns überlegt, jeder natürlichen Zahl $n$ ihre Hälfte $\frac{n}{2}$ zuzuordnen. Damit können wir links und rechts des Zuordnungspfeils nun einfach diese beliebige natürliche Zahl $n$ bzw. die sich daraus ergebende rationale Zahl $\frac{n}{2}$ hinschreiben:

${\displaystyle n⟼\frac{n}{2}\hspace{0.5em}.}$
Man liest dies als ,,$n$ wird auf $\frac{n}{2}$ abgebildet". Diese Schreibweise bezeichnet man auch als Abbildungsvorschrift der Funktion. Eine weitere Schreibweise für die Abbildungsvorschrift benutzt den Namen der Funktion:

${\displaystyle f(n)=\frac{n}{2}\hspace{0.5em}.}$
Man liest dies als ,,$f$ von $n$ ist gleich $\frac{n}{2}$". Wir können also die hier betrachtete Funktion $f$ nun zusammengefasst folgendermaßen schreiben:

${\displaystyle f:\mathrm{\hspace{0.5em}\hspace{0.5em}}\{\begin{array}{ccc}\hfill \mathbb{N}& \hfill \to \hfill & \mathbb{Q}\hfill \\ \hfill n& \hfill ⟼\hfill & \frac{n}{2}\hspace{0.5em}.\hfill \end{array}}$
Man liest dies nun als ,,die Funktion $f$ bildet von $\mathbb{N}$ nach $\mathbb{Q}$ ab, jedes $n\in \mathbb{N}$ wird auf $\frac{n}{2}\in \mathbb{Q}$ abgebildet". Diese zusammenfassende Schreibweise werden wir im Rest dieses Moduls für Funktionen weiter verwenden.
Wir betrachten einige weitere einfache Beispiele für Funktionen:


Die obigen Beispiele zeigen einige Grundeigenschaften von Funktionen, für die wir nun spezielle Begriffe einführen wollen:

Betrachten wir die Abbildungsvorschrift $h(x)=\frac{1}{x}$ der Funktion $h$, so sehen wir, dass eigentlich nichts dagegen spricht, jede beliebige reelle Zahl für $x$ in $\frac{1}{x}$ einzusetzen außer der Zahl $x=0$, da die Rechenoperation ,,$\frac{1}{0}$" kein Ergebnis liefert. Man kann bei der Angabe einer Definitionsmenge also unterscheiden zwischen Zahlen, die ausgeschlossen sind, da man sie überhaupt nicht in die Abbildungsvorschrift einsetzen darf, und solchen, die ausgeschlossen sind, weil die Funktion eben so definiert ist. Dies führt nun auf den Begriff des größtmöglichen Definitionsbereichs einer Funktion, der größtmöglichen Teilmenge der reellen Zahlen $ℝ$, die man als Definitionsmenge einer Funktion mit bekannter Abbildungsvorschrift benutzen kann.


Beim Aufschreiben von Funktionen ist neben dem Definitionsbereich noch eine zweite Menge notwendig, nämlich diejenige Menge, die das Ziel der durch die Funktion beschriebenen Zuordnung ist. Diese wird als Zielmenge oder Zielbereich bezeichnet. Betrachten wir nochmal die Funktion

${\displaystyle \phi :\mathrm{\hspace{0.5em}\hspace{0.5em}}\{\begin{array}{ccc}\hfill (0;1)& \hfill \to \hfill & ℝ\hfill \\ \hfill y& \hfill ⟼\hfill & 3y+1\hfill \end{array}}$
aus Beispiel 6.1.4. Deren Zielmenge sind die reellen Zahlen $ℝ$. Die Zielmenge der Funktion

${\displaystyle f:\mathrm{\hspace{0.5em}\hspace{0.5em}}\{\begin{array}{ccc}\hfill \mathbb{N}& \hfill \to \hfill & \mathbb{Q}\hfill \\ \hfill n& \hfill ⟼\hfill & \frac{n}{2}\hfill \end{array}}$
aus dem einführenden Beispiel dieses Abschnitts sind die rationalen Zahlen $\mathbb{Q}$. Wir erkennen hier einen wichtigen Unterschied zwischen der Definitionsmenge und der Zielmenge einer Funktion. Die Definitionsmenge enthält alle Zahlen, und nur diese, die man in die Abbildungsvorschrift der Funktion einsetzen darf und möchte. Wohingegen die Zielmenge alle Zahlen enthalten kann, die potentiell als Ergebnis der Abbildungsvorschrift auftauchen können.
In diesem Zusammenhang stellen wir uns die Frage, was denn der kleinstmögliche Zielbereich ist, den man für eine Funktion mit gegebenem Definitionsbereich und bekannter Abbildungsvorschrift benutzen kann. Unter dem kleinstmöglichen Zielbereich verstehen wir all diejenigen Zahlen, die - bei gegebener Definitionsmenge und Abbildungsvorschrift - tatsächlich als Ziele der Zuordnung auftauchen. Diese Menge bezeichnet man als Wertebereich oder Wertemenge und dessen Elemente als Werte der Funktion. Für eine Funktion $f$ benutzt man das Symbol $W_f$ für die Wertemenge. Für die Werte einer Funktion $f$ mit Veränderlicher $x$ schreibt man allgemein meist $f(x)\in W_f$, wie in der Abbildungsvorschrift, oder führt eine weitere Variable ein, zum Beispiel $y=f(x)\in W_f$.

Solche Wertetabellen sind sinnvoll, um sich einen Überblick über die Werte einer Funktion zu verschaffen. Sie reichen aber nicht aus, um mathematisch ganz sicher zu sein, was der tatsächliche Wertebereich einer Funktion ist. Eine Methode, den Wertebereich einer Funktion zu bestimmen, benutzt das Lösen von Ungleichungen: