Kapitel 6 Elementare Funktionen

Abschnitt 6.2 Lineare Funktionen und Polynome

6.2.9 Gebrochenrationale Funktionen

Allgemeine gebrochenrationale Funktionen besitzen Abbildungsvorschriften, die aus dem Quotienten zweier Polynome bestehen. Hier einige Beispiele mit ihren Graphen. Natürlich müssen auch bei diesen Funktionen diejenigen Zahlen aus dem Definitionsbereich ausgeschlossen werden, für die der Nenner in der Abbildungsvorschrift gleich Null wird.



Die Nullstellen einer gebrochenrationalen Funktion ergeben sich als die Zählernullstellen. So hat zum Beispiel die Funktion

${\displaystyle j:\mathrm{\hspace{0.5em}\hspace{0.5em}}\{\begin{array}{ccc}\hfill ℝ\setminus \{-1;3\}& \hfill \to \hfill & ℝ\hfill \\ \hfill x& \hfill ⟼\hfill & \frac{x-1}{x^2-2x-3}\hfill \end{array}}$
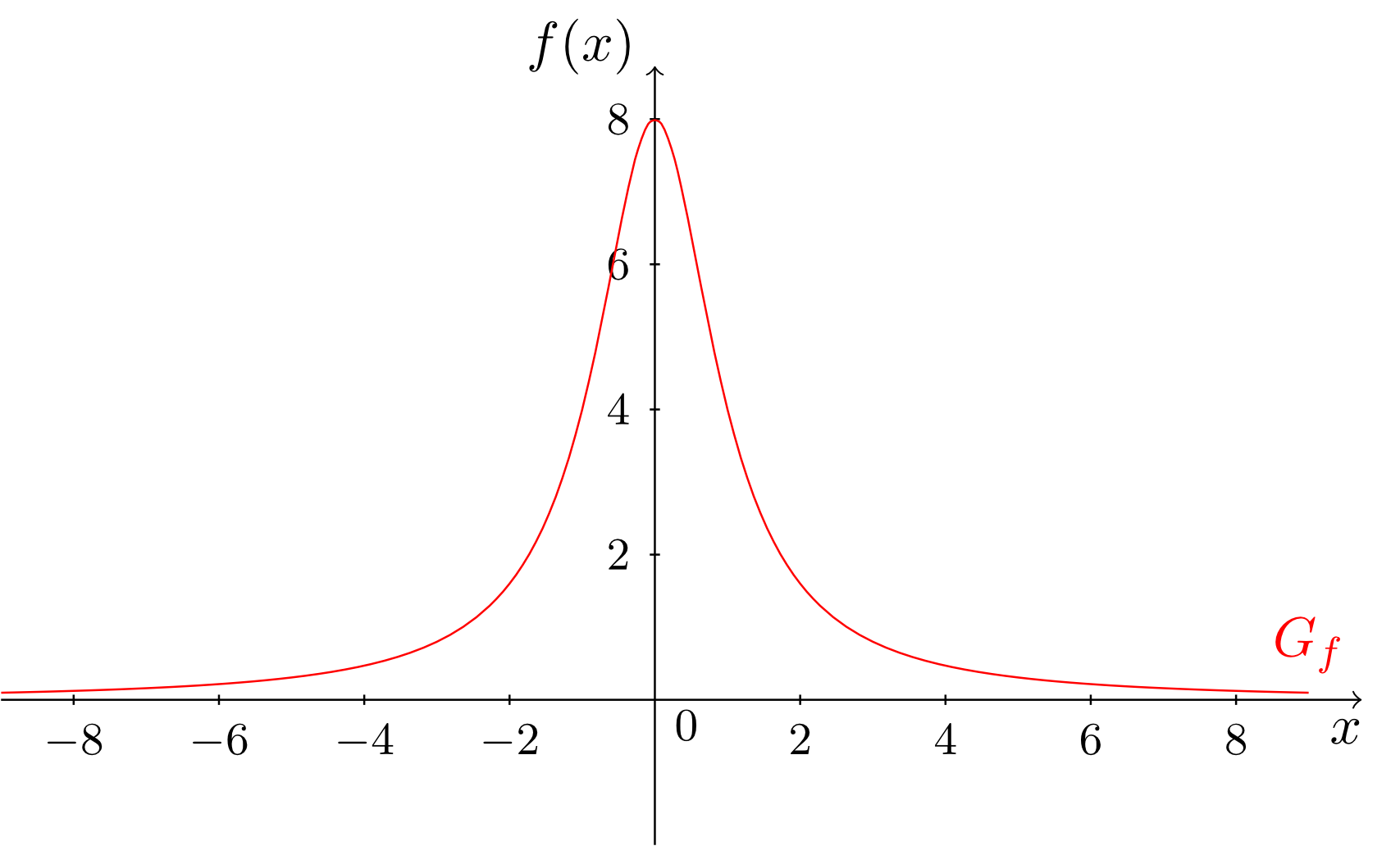
die einzige Nullstelle bei $x=1$. Die Nennernullstellen gebrochenrationaler Funktionen, welche aus dem Definitionsbereich ausgeschlossen werden, müssen oft noch genauer untersucht werden. Vor allem ist von Interesse, wie die Graphen der Funktionen in der Nähe der Definitionslücken verlaufen. Die Nennernullstellen gebrochenrationaler Funktionen bezeichnet man auch als Polstellen. Die folgenden Beispiele zeigen, dass es verschiedene Typen von Polstellen gibt.

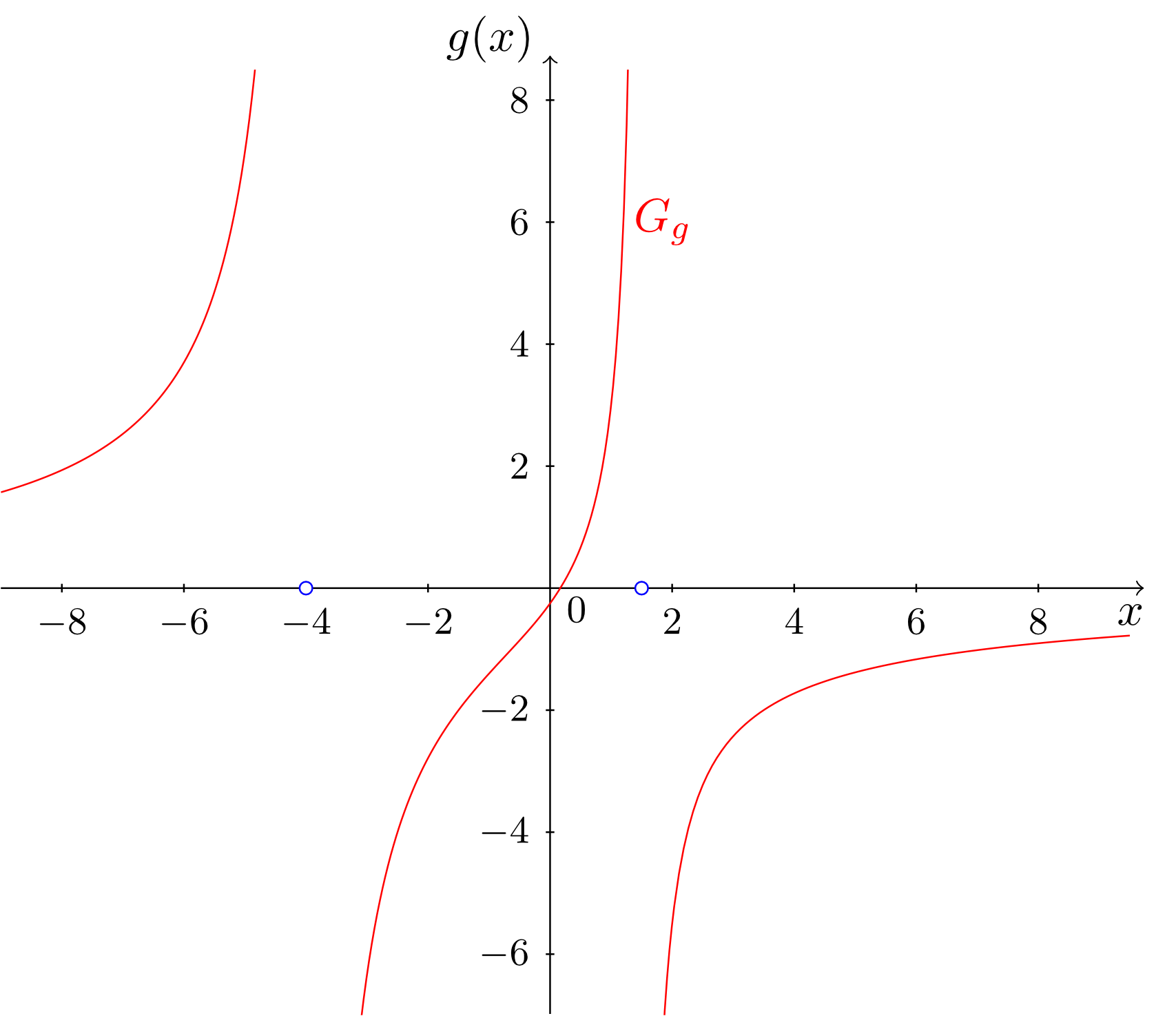
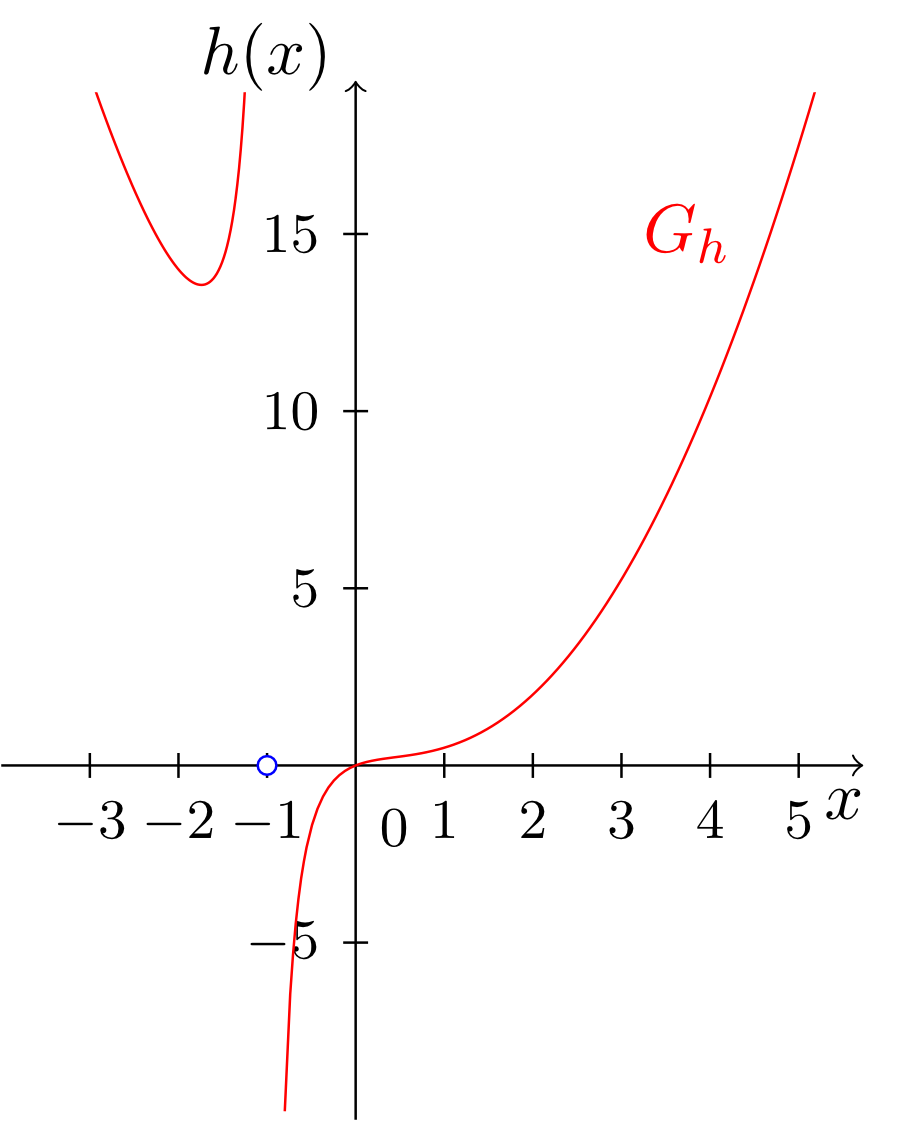
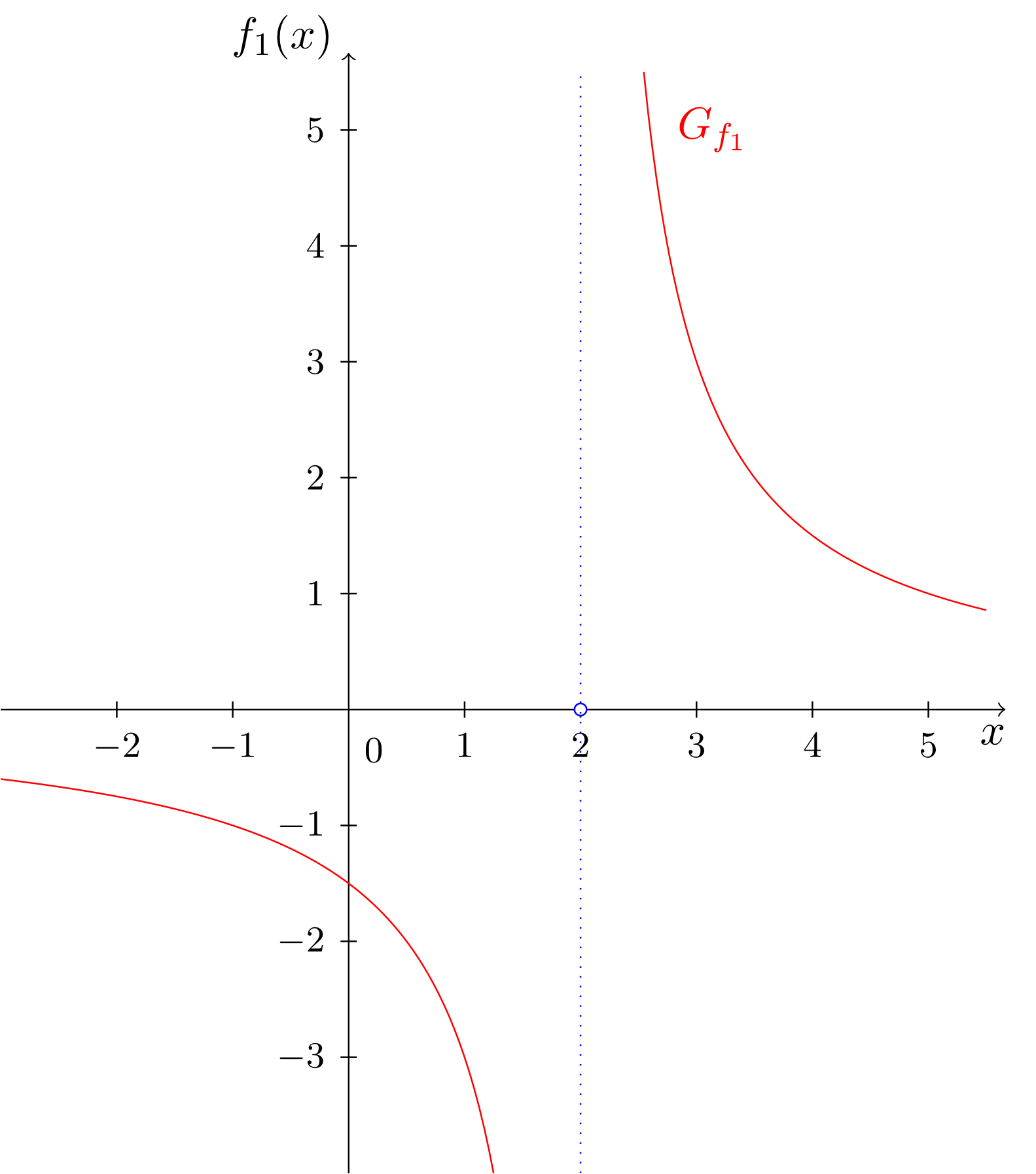
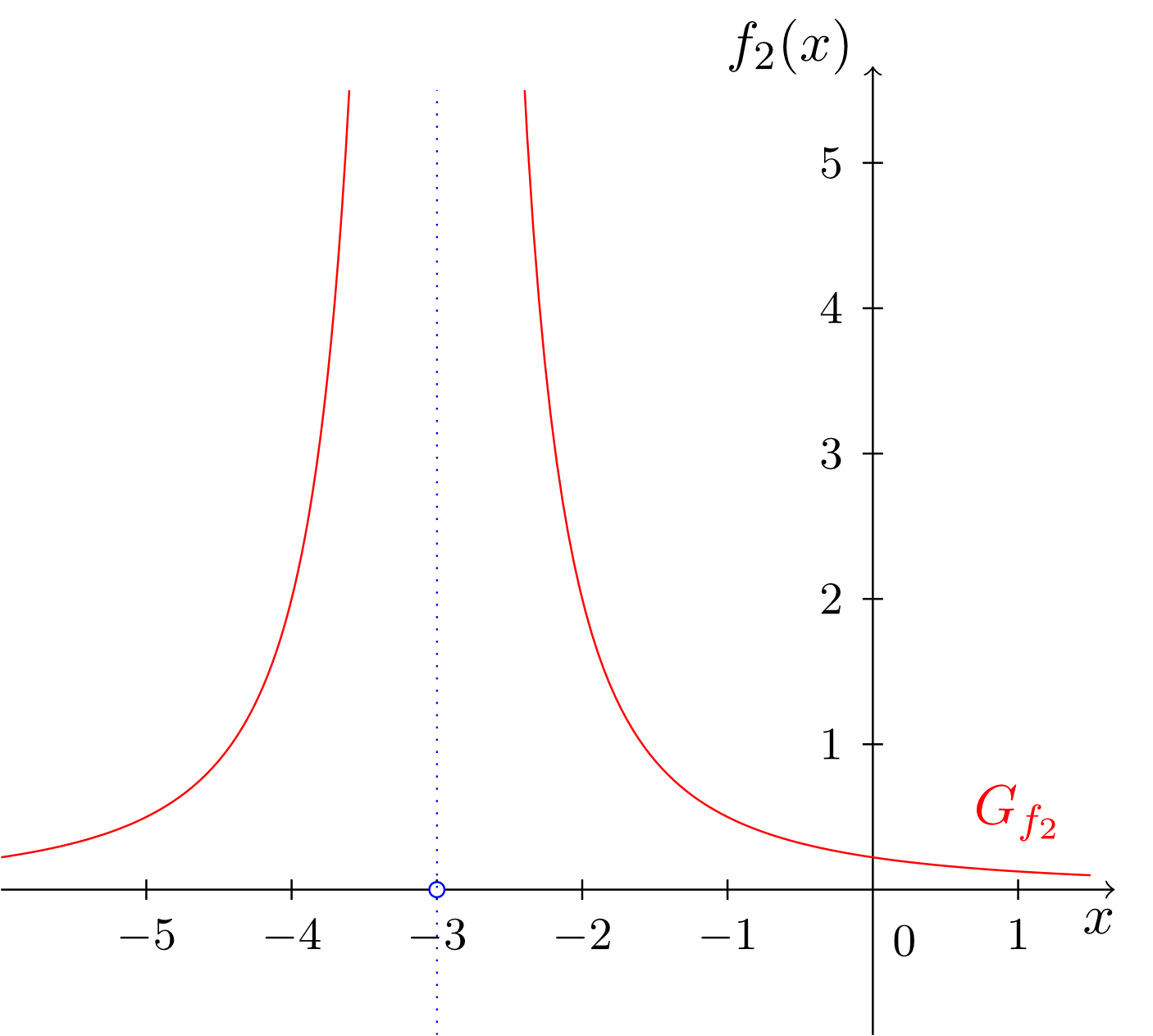
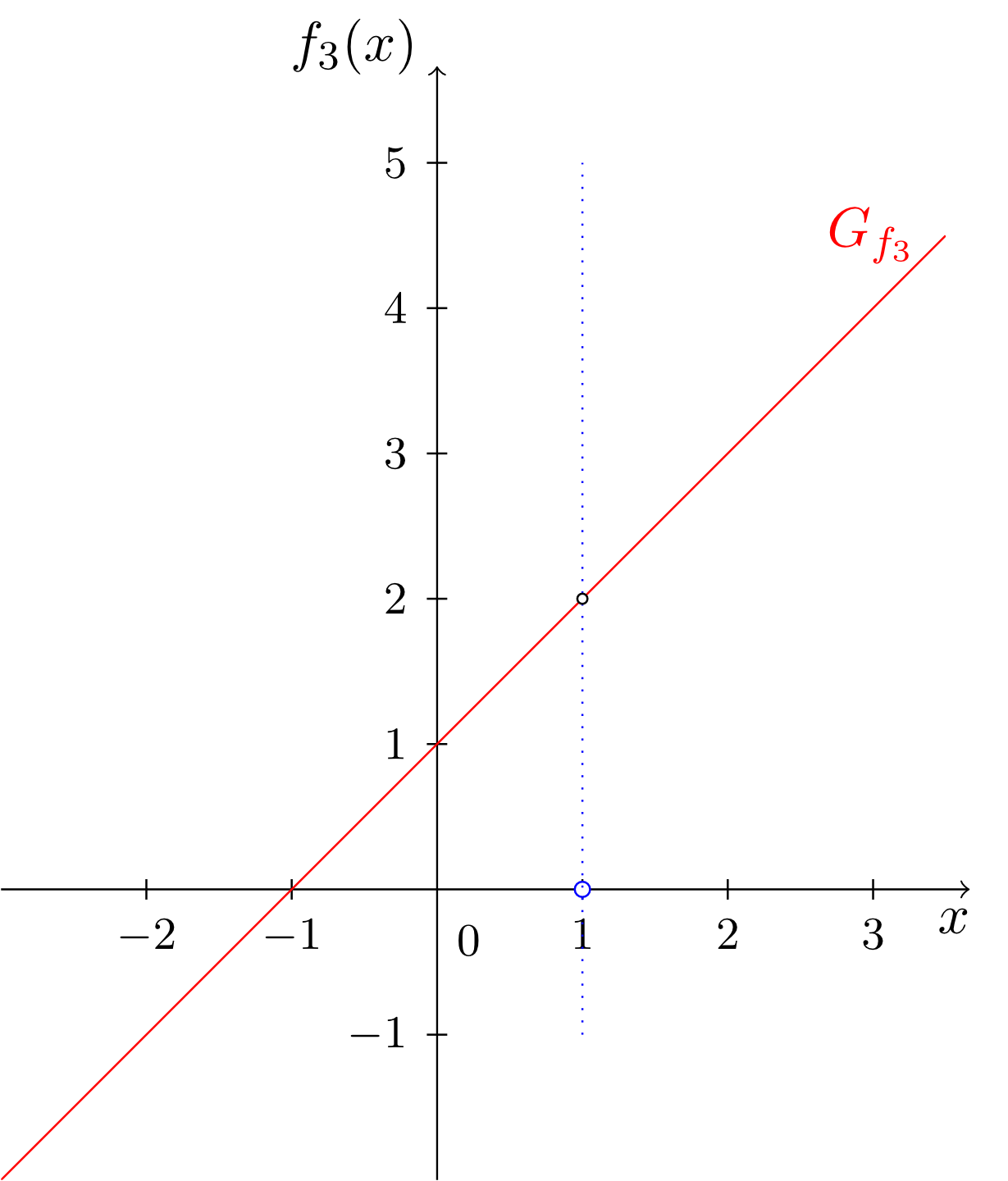
Die Stellen $x=2$ und $x=-3$ sind sogenannte echte Polstellen der Funktionen $f_1$ und $f_2$, die Stelle $x=1$ ist eine sogenannte hebbare Definitionslücke der Funktion $f_3$. Anhand der Graphen wird der Unterschied zwischen diesen Typen von Polstellen deutlich. Bei echten Polstellen wächst oder fällt der Graph in der Nähe der Polstelle unbeschränkt, und bei hebbaren Definitionslücken mündet er von links und rechts in das ,,Loch" im Graphen ein.
Anhand der Abbildungsvorschriften der drei Funktionen kommt dieser Unterschied folgendermaßen zum Ausdruck: Die Werte $x=2$ und $x=-3$ sind Nennernullstellen, aber keine Zählernullstellen der Funktionen $f_1$ bzw. $f_2$. Tatsächlich besitzen $f_1$ und $f_2$ gar keine Zählernullstellen. In einem solchen Fall sind die Nennernullstellen immer echte Polstellen.

Ein weiterer Unterschied wird zwischen den beiden Polstellen von $f_1$ und $f_2$ deutlich. Bei der Polstelle $x=2$ von $f_1$ findet ein Vorzeichenwechsel der Funktion statt. Der Graph von $f_1$ fällt links der Polstelle unbeschränkt ins Negative und wächst rechts der Polstelle (von rechts kommend) unbeschränkt ins Positive.
Der Graph von $f_2$ wächst auf beiden Seiten der Polstelle $x=-3$ (bei Annäherung an diese) ins Positive, es findet also kein Vorzeichenwechsel statt.
In der Abbildungsvorschrift von $f_3$ hingegen kann man den Term, der dafür verantwortlich ist, dass man die Polstelle $x=1$ nicht einsetzen darf, herauskürzen. Dies ist bei gebrochenrationalen Funktionen, die eine hebbare Definitionslücke als Polstelle aufweisen, immer so.