10.2.1 Introduction

In this section vectors are used (first of all) to describe lines in the plane. Then we will see that this description of lines can be extended to the three-dimensional case. Besides lines, there are other mathematical objects in space which can easily be described by means of vectors, namely planes. Finally, we will discuss the possible relative positions of points, lines, and planes with respect to each other.
For this purpose, the concepts outlined in the Info Box below are important.

Further contents
The following considerations and figures illustrate why the concepts of collinearity and coplanarity are relevant for the investigation of lines and planes.
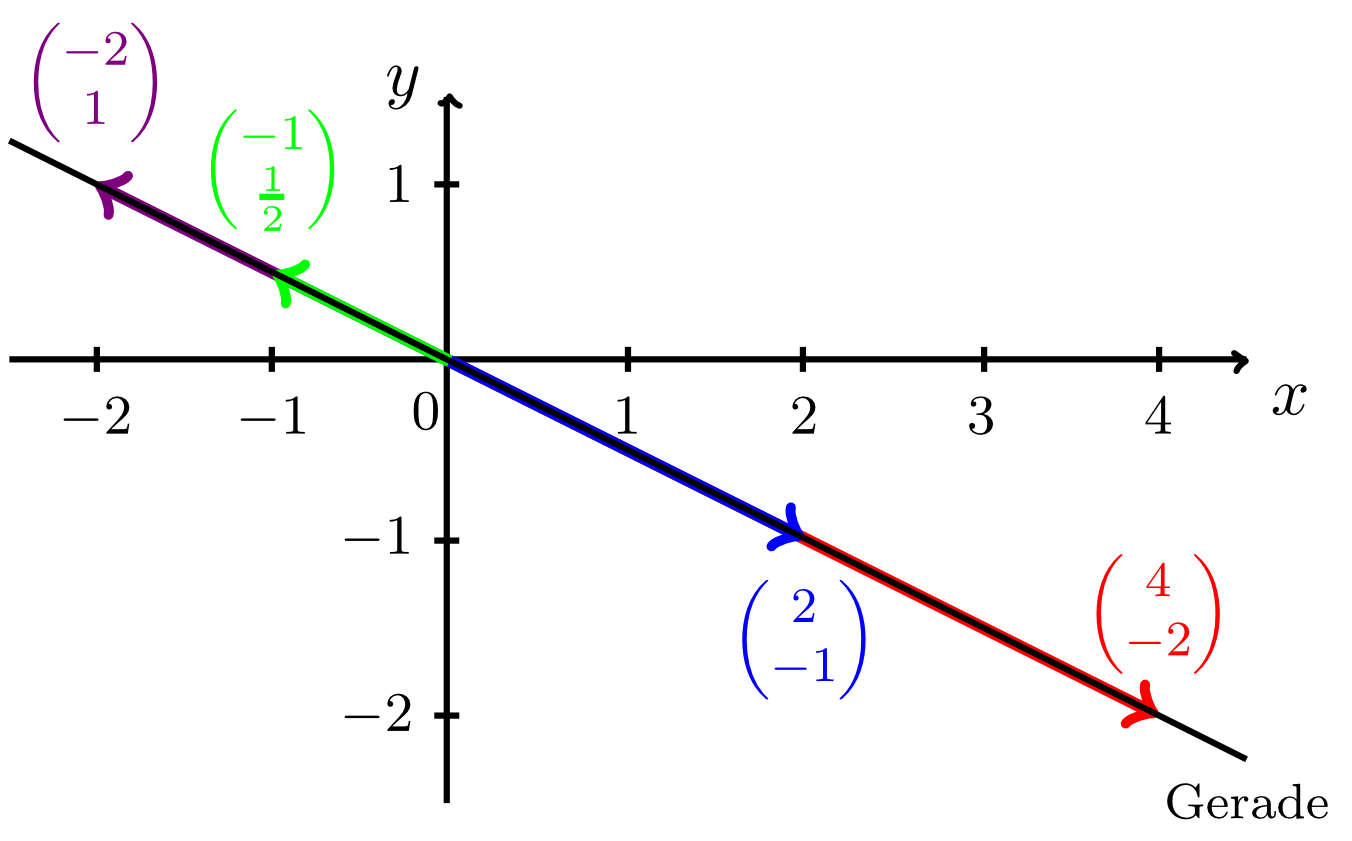
Collinear vectors are multiples of each other. The representatives of collinear vectors with the same initial point lie on the same line. For example, the vectors

${\displaystyle \overrightarrow{x}=\left(\begin{array}{c}\hfill 2\hfill \\ \hfill -1\hfill \end{array}\right)}$
and

${\displaystyle \overrightarrow{y}=\left(\begin{array}{c}\hfill -1\hfill \\ \hfill \frac{1}{2}\hfill \end{array}\right)}$
are collinear since

${\displaystyle \overrightarrow{y}=\left(\begin{array}{c}\hfill -1\hfill \\ \hfill \frac{1}{2}\hfill \end{array}\right)=-\frac{1}{2}\left(\begin{array}{c}\hfill 2\hfill \\ \hfill -1\hfill \end{array}\right)=-\frac{1}{2}\overrightarrow{x}}$
(or also $\overrightarrow{x}=-2\overrightarrow{y}$). Further vectors that are collinear to both $\overrightarrow{x}$ and $\overrightarrow{y}$ are, for example, $\left(\begin{array}{c}\hfill 4\hfill \\ \hfill -2\hfill \end{array}\right)$ or $\left(\begin{array}{c}\hfill -2\hfill \\ \hfill 1\hfill \end{array}\right)$. In contrast, the vector $\left(\begin{array}{c}\hfill 1\hfill \\ \hfill 1\hfill \end{array}\right)$ is not collinear to $\overrightarrow{x}$ (and hence not collinear to $\overrightarrow{y}$) since there cannot be any number $s\in ℝ$ that satisfies the equation

${\displaystyle \overrightarrow{x}=\left(\begin{array}{c}\hfill 2\hfill \\ \hfill -1\hfill \end{array}\right)=s\left(\begin{array}{c}\hfill 1\hfill \\ \hfill 1\hfill \end{array}\right)\hspace{0.5em}.}$
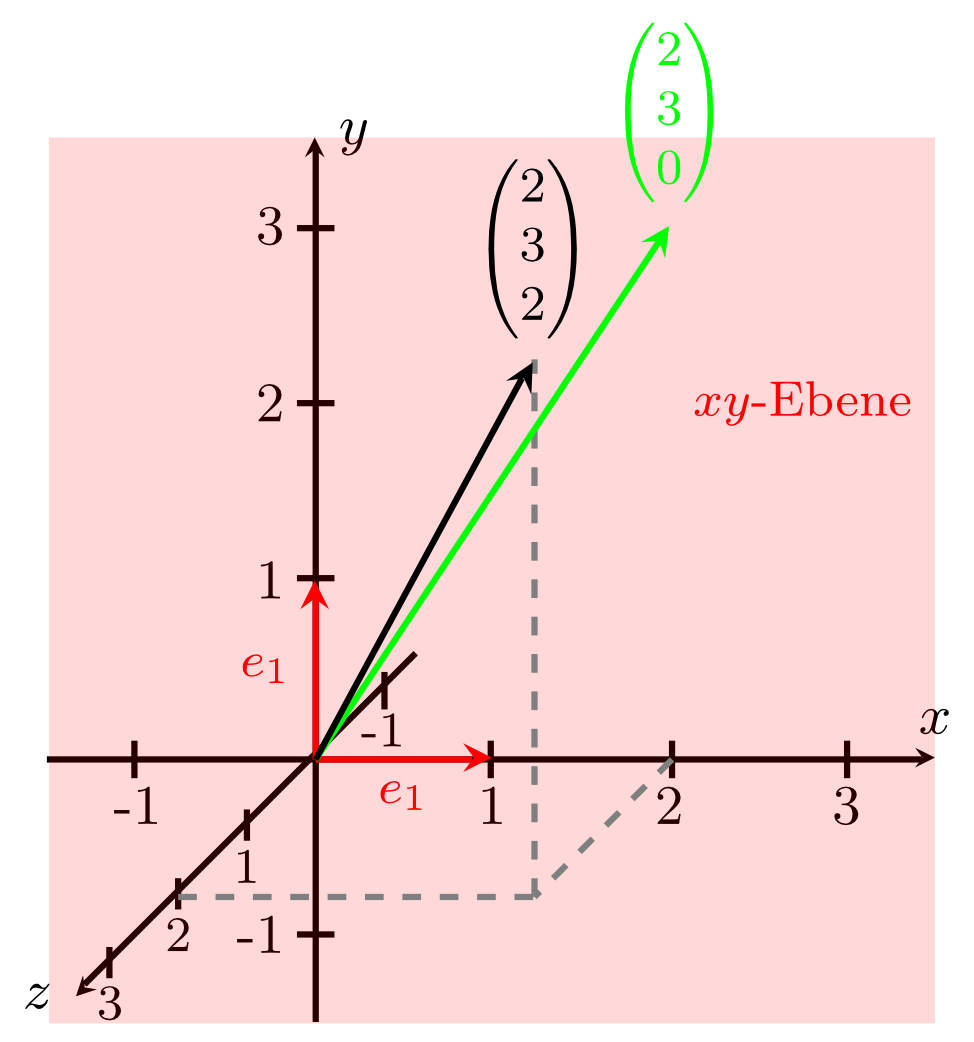
Representatives of collinear vectors with the same initial point, such as the arrows of the corresponding position vectors (see figure below), all lie on the same line. For coplanar vectors in space, their representatives lie in the same plane if they have the same initial point. For example, the vectors

${\displaystyle {\overrightarrow{e}}_1=\left(\begin{array}{c}\hfill 1\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \end{array}\right)\hspace{0.5em},\hspace{0.5em}\hspace{0.5em}{\overrightarrow{e}}_2=\left(\begin{array}{c}\hfill 0\hfill \\ \hfill 1\hfill \\ \hfill 0\hfill \end{array}\right)\hspace{0.5em}\text{and}\hspace{0.5em}\left(\begin{array}{c}\hfill 2\hfill \\ \hfill 3\hfill \\ \hfill 0\hfill \end{array}\right)}$
are coplanar since

${\displaystyle \left(\begin{array}{c}\hfill 2\hfill \\ \hfill 3\hfill \\ \hfill 0\hfill \end{array}\right)=2{\overrightarrow{e}}_1+3{\overrightarrow{e}}_2=2\left(\begin{array}{c}\hfill 1\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \end{array}\right)+3\left(\begin{array}{c}\hfill 0\hfill \\ \hfill 1\hfill \\ \hfill 0\hfill \end{array}\right)\hspace{0.5em}.}$
The arrows of their corresponding position vectors all lie in the $xy$-plane of a coordinate system in space. In contrast, the vectors

${\displaystyle {\overrightarrow{e}}_1=\left(\begin{array}{c}\hfill 1\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \end{array}\right),\hspace{0.5em}{\overrightarrow{e}}_2=\left(\begin{array}{c}\hfill 0\hfill \\ \hfill 1\hfill \\ \hfill 0\hfill \end{array}\right)\hspace{0.5em},\text{and}\hspace{0.5em}\left(\begin{array}{c}\hfill 2\hfill \\ \hfill 3\hfill \\ \hfill 2\hfill \end{array}\right)}$
are not coplanar since the vector $\left(\begin{array}{c}\hfill 2\hfill \\ \hfill 3\hfill \\ \hfill 2\hfill \end{array}\right)$ has a non-zero $z$-component, i.e. all its representatives are perpendicular to the $xy$-plane. It can easily be seen that there cannot be any numbers $s,t\in ℝ$ such that the equation

${\displaystyle \left(\begin{array}{c}\hfill 2\hfill \\ \hfill 3\hfill \\ \hfill 2\hfill \end{array}\right)=s\left(\begin{array}{c}\hfill 1\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \end{array}\right)+t\left(\begin{array}{c}\hfill 0\hfill \\ \hfill 1\hfill \\ \hfill 0\hfill \end{array}\right)}$
is satisfied. This is illustrated in the figure below.