Chapter 10 Basic Concepts of Descriptive Vector Geometry

Section 10.1 From Arrows to Vectors

10.1.2 Coordinate Systems in Three-Dimensional Space

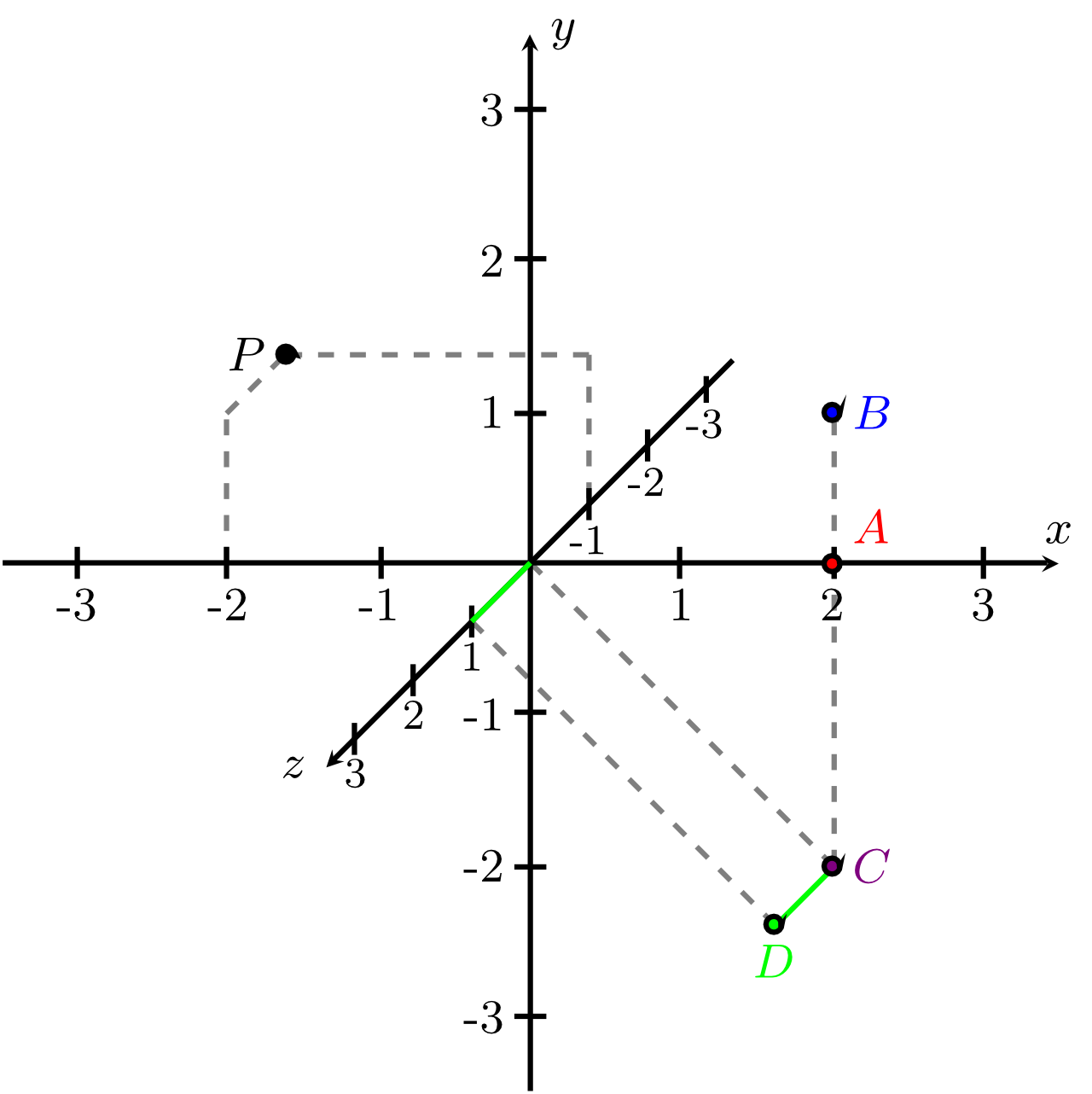
In Section 9.1 of the previous Module 9 we introduced Cartesian coordinate systems and points in the plane described by coordinates with respect to these coordinate systems. A solid understanding of these concepts is now presumed in this Module. To describe a point in three-dimensional space, three coordinates are required. Thus, a coordinate system in three-dimensional space needs three axes, the $x$-axis, $y$-axis and $z$-axis (sometimes called the $x_1$-axis, $x_2$-axis, and $x_3$-axis). Usually, points will be denoted by upper-case Latin letters $P,Q,R,\dots$, and their coordinates will be denoted by lower-case Latin letters $a,b,c,x,y,z,\dots$ as variables. Extending the notation from Module 9, the coordinates of a point are written, for example, as follows:

${\displaystyle P=(1;3;0)}$
or

${\displaystyle Q=(-2;2;3)\hspace{0.5em}.}$
Here, the $x$-coordinate of the point $Q$ is $-2$, its $y$-coordinate is $2$ and its $z$-coordinate is $3$. The point with the coordinates $(0;0;0)$ is called the origin, and it is denoted by the symbol $O$. All these points are drawn in the figure below.
The dashed lines in this figure indicate how the coordinates of points in such a three-dimensional representation can be drawn and read off. Note that these lines are all parallel to the coordinate axes.
We will only consider coordinate systems in three-dimensional space with perpendicular coordinate axes - these are Cartesian coordinate systems. Furthermore, we will use the common mathematical convention that coordinate systems in three-dimensional space are right-handed. Sometimes these are also called positively oriented. This means that the positive directions of the $x$, $y$, and $z$-axis can be determined by means of the right-hand rule as illustrated in the figure below.

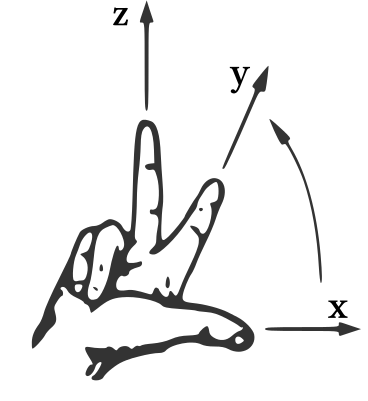
However, there are various possible representations. In the figure above showing the points $P$ and $Q$, the $x$-axis points to the right, the $y$-axis points up, and the $z$-axis points perpendicularly outwards from the drawing plane. In the figure which illustrates the right-hand rule, the $x$-axis points to the right, the $y$-axis points backwards into the drawing plane, and the $z$-axis points up. However, both coordinate systems are right-handed.

As in the two-dimensional case discussed in Section 9.1.2, an arbitrary number of points in three-dimensional space can be collected into a set of points. The following notation is used: