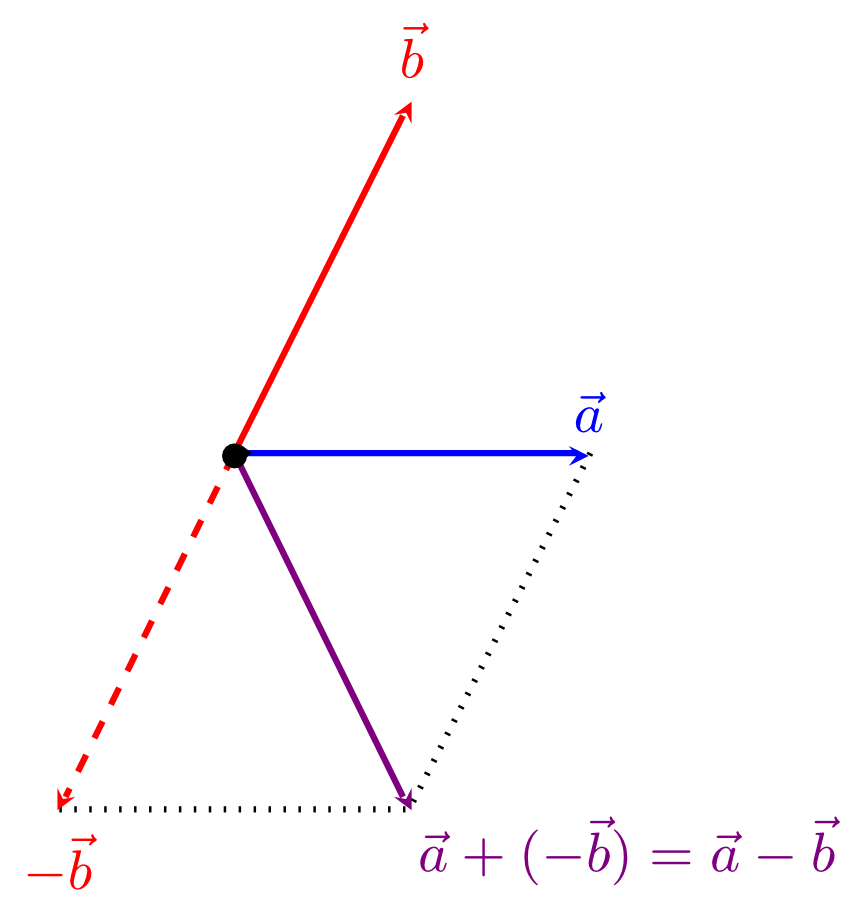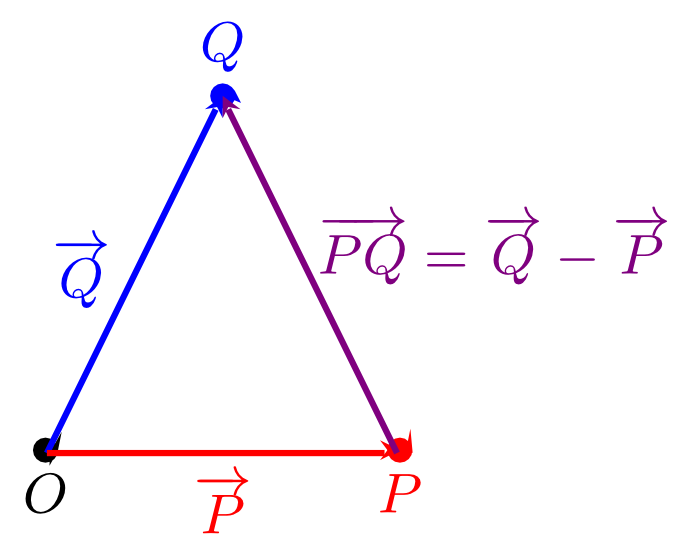Chapter 10 Basic Concepts of Descriptive Vector Geometry

Section 10.1 From Arrows to Vectors

10.1.4 Simple Vector Operations

In this section we discuss what kinds of vector operations we can carry out on the vectors introduced in the previous Section 10.1.3. We can view vector operations in two different ways. First you can carry out the vector operations of addition, subtraction and - with a certain restriction - multiplication on vectors specified as

2

- or

3

-tuples. On the other hand, these operations can be interpreted graphically with respect to the arrows representing the vectors. That is, the vector operations on vectors can be interpreted as geometric operations on their representatives. This geometric interpretation of vector operations leads to a deeper understanding of position vectors and connecting vectors of points.
Vector operations in two and three dimensions are carried out in essentially the same way. For all component-wise vector operations presented below both cases (two-dimensional and three-dimensional) are considered. The corresponding figures illustrate the geometric interpretation of the operations on the representatives of the vectors and visualise the position and connecting vectors. They will mostly show only arrows and points without a coordinate system. In this way, the figures apply to both the two-dimensional and the three-dimensional case.
Since vectors will be transformed below by equivalent transformations into each other, we need to specify under which conditions two vectors are considered to be equal.

Info 10.1.8

Two vectors

\vec{a}, \vec{b} \in ℝ^{2} or ℝ^{3}

are equal (written as

\vec{a} = \vec{b}

) if and only if they satisfy one (and hence all) of the following equivalent conditions:

$\vec{a}$ and $\vec{b}$ have the same components:

$\vec{a} = \vec{b} \Leftrightarrow (\begin{matrix} a_{x} \\ a_{y} \end{matrix}) = (\begin{matrix} b_{x} \\ b_{y} \end{matrix}) \Leftrightarrow a_{x} = b_{x} and a_{y} = b_{y}$
in the two-dimensional case or

$\vec{a} = \vec{b} \Leftrightarrow (\begin{matrix} a_{x} \\ a_{y} \\ a_{z} \end{matrix}) = (\begin{matrix} b_{x} \\ b_{y} \\ b_{z} \end{matrix}) \Leftrightarrow a_{x} = b_{x} and a_{y} = b_{y} and a_{z} = b_{z}$
in the three-dimensional case. This is also known as comparison of coordinates or components.
$\vec{a}$ and $\vec{b}$ have the same representatives.
$\vec{a}$ and $\vec{b}$ are both the position vector of the same point.
$\vec{a}$ and $\vec{b}$ are both the connecting vector of the same two points.

From the statements in the Info Box above we see that two vectors of different dimensions (i.e.

\vec{a} \in ℝ^{2}

and

\vec{b} \in ℝ^{3}

) can never be equal. Since these vectors have a different number of components, they are not even comparable. Thus, vector operations are only carried out on vectors with an equal number (two or three) of components , and these operations will always result in a vector with this fixed number of components.

Info 10.1.9

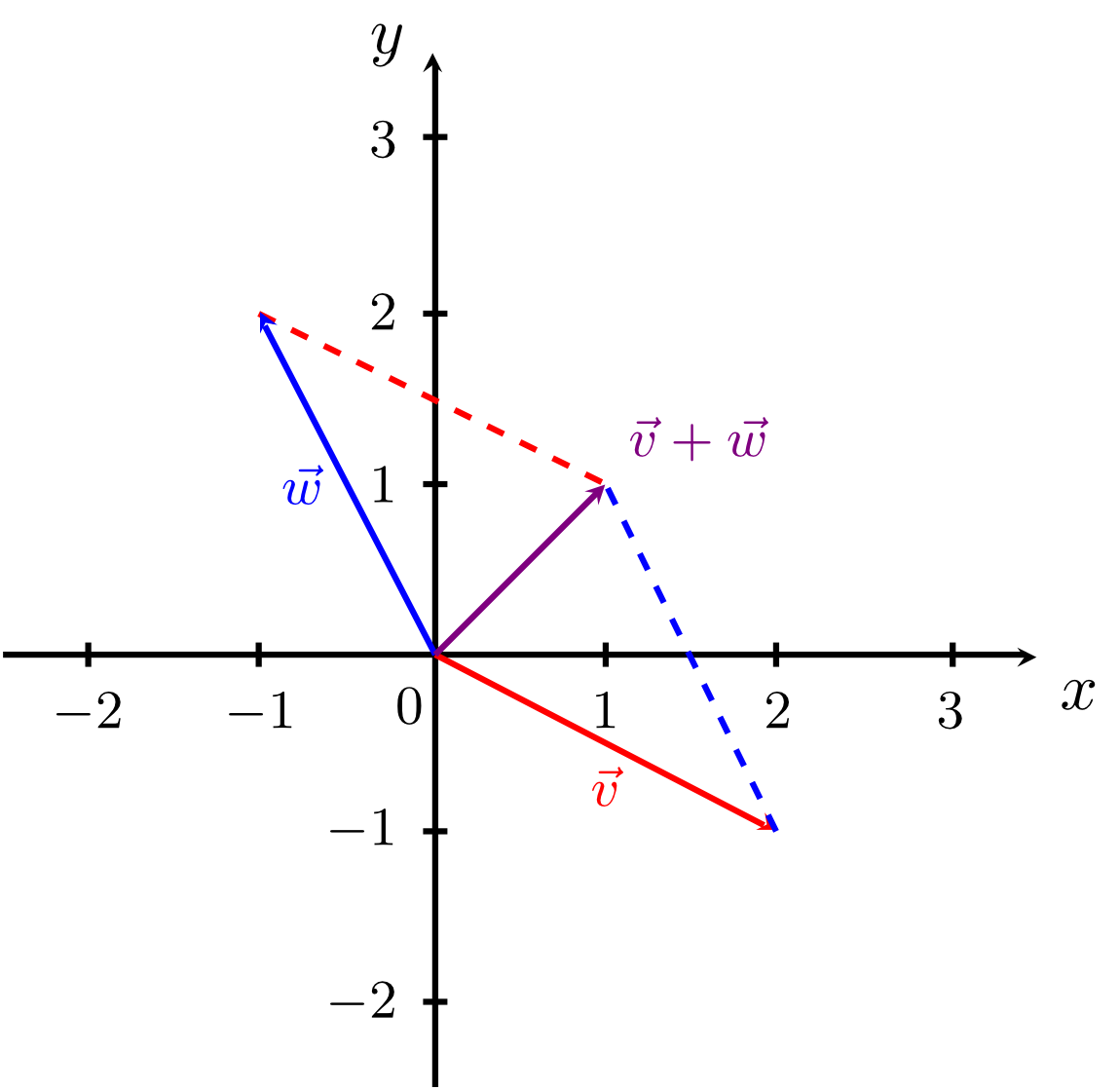
The addition of two vectors involves the addition of all their components, i.e.

\vec{a} + \vec{b} = (\begin{matrix} a_{x} \\ a_{y} \end{matrix}) + (\begin{matrix} b_{x} \\ b_{y} \end{matrix}) = (\begin{matrix} a_{x} + b_{x} \\ a_{y} + b_{y} \end{matrix})

in the two-dimensional case and

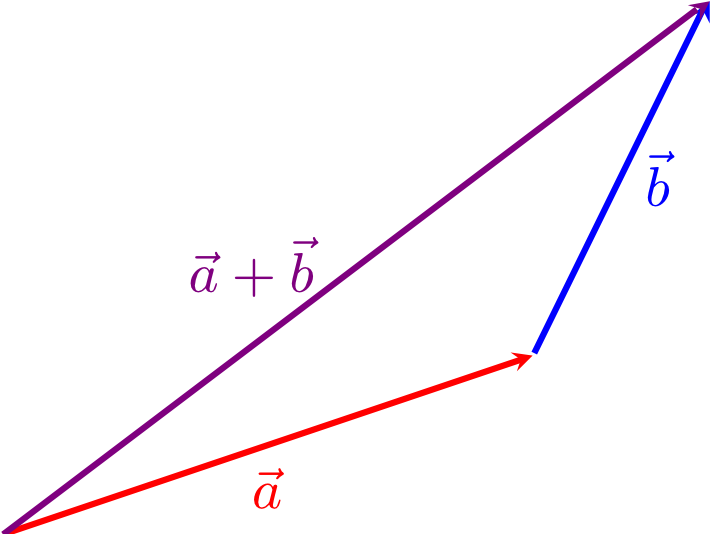
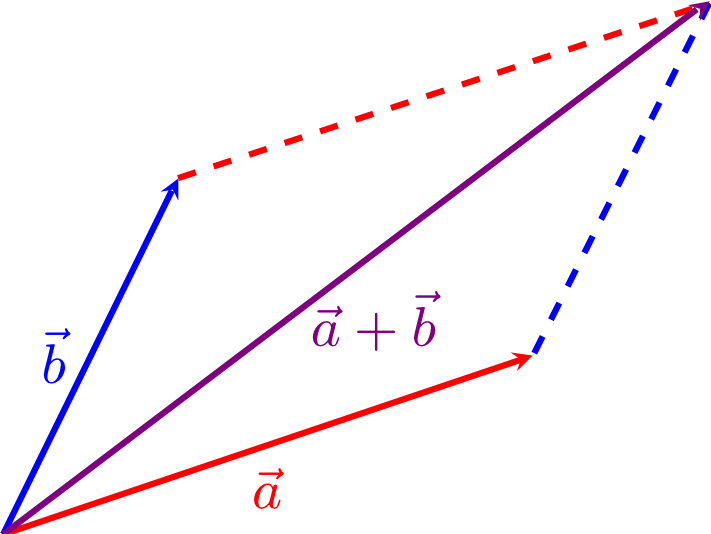
\vec{a} + \vec{b} = (\begin{matrix} a_{x} \\ a_{y} \\ a_{z} \end{matrix}) + (\begin{matrix} b_{x} \\ b_{y} \\ b_{z} \end{matrix}) = (\begin{matrix} a_{x} + b_{x} \\ a_{y} + b_{y} \\ a_{z} + b_{z} \end{matrix})

in the three-dimensional case. Geometrically, vector addition can be interpreted as either a"linking" of two arrows or a completion of two arrows to a parallelogram, depending on which representatives of the vectors are used:

The laws of associativity and commutativity apply to the addition of two vectors as to the addition of real numbers (see Section 1.1.3):

\vec{a} + \vec{b} = \vec{b} + \vec{a}

and

\vec{a} + \vec{b} + \vec{c} = (\vec{a} + \vec{b}) + \vec{c} = \vec{a} + (\vec{b} + \vec{c}) .

The zero vector

\vec{O} = (\begin{matrix} 0 \\ 0 \end{matrix})

\vec{O} = (\begin{matrix} 0 \\ 0 \\ 0 \end{matrix})

plays the same role for vectors as the number

0

for the real numbers:

\vec{a} + \vec{O} = \vec{O} + \vec{a} = \vec{a} .

Example 10.1.10

Consider two vectors

\vec{v} = (\begin{matrix} 2 \\ - 1 \end{matrix})

and

\vec{w} = (\begin{matrix} - 1 \\ 2 \end{matrix})

. Then, we have

\vec{v} + \vec{w} = (\begin{matrix} 2 \\ - 1 \end{matrix}) + (\begin{matrix} - 1 \\ 2 \end{matrix}) = (\begin{matrix} 2 - 1 \\ - 1 + 2 \end{matrix}) = (\begin{matrix} 1 \\ 1 \end{matrix}) .

This is illustrated by the figure below.

Furthermore,

\vec{w}

is the connecting vector from the point

P = (2; 0)

to the point

Q = (1; 2)

, i.e.

\vec{w} = \vec{P Q}

, and

\vec{v}

is the connecting vector from the point

Q = (1; 2)

to the point

R = (3; 1)

, i.e.

\vec{v} = \vec{Q R}

\vec{w} + \vec{v} = \vec{P Q} + \vec{Q R} = \vec{P R} .

This is illustrated by the figure below.

The example above shows that expressions for connecting vectors of points can also be simplified by means of vector operations. This will be discussed for the subtraction of vectors in more detail below.

Exercise 10.1.11

Let the vectors $\vec{u} = (\begin{matrix} 1 \\ 0 \\ - 8 \end{matrix})$ and $\vec{v} = (\begin{matrix} - 3 \\ - 4 \\ 3 \end{matrix})$ be given. Calculate $\vec{v} + \vec{u}$ .
$\vec{v} + \vec{u} =$
Let the points $P$ , $Q$ , and $R$ be given. Which of the following expressions are equivalent to the expression $(\vec{P} + \vec{P Q}) + \vec{Q R}$ ?

$\vec{P} + (\vec{P Q} + \vec{Q R})$

$\vec{P R}$

$\vec{Q R}$

$\vec{O R}$

$\vec{R}$

$\vec{Q} + \vec{Q R}$

$\vec{v} + \vec{u} = (\begin{matrix} - 3 \\ - 4 \\ 3 \end{matrix}) + (\begin{matrix} 1 \\ 0 \\ - 8 \end{matrix}) = (\begin{matrix} - 3 + 1 \\ - 4 + 0 \\ 3 - 8 \end{matrix}) = (\begin{matrix} - 2 \\ - 4 \\ - 5 \end{matrix}) .$
$(\vec{P} + \vec{P Q}) + \vec{Q R} = \vec{P} + (\vec{P Q} + \vec{Q R}) (associativity)$

$= (\vec{O P} + \vec{P Q}) + \vec{Q R} = \vec{O Q} + \vec{Q R} = \vec{Q} + \vec{Q R} = \vec{O R} = \vec{R} .$

When we study possible operations on vectors further, we will see that the component-wise multiplication or division of vectors is not a meaningful operation. To understand this, however, would go far beyond the scope of this course. At this point you simply have to accept that vectors cannot be multiplied that simply, let alone divided. What we certainly can do is multiply vectors by real numbers and - based on that - subtract vectors. Please note: if we speak of the length of a vector in the following section, we mean the geometric length of the arrows representing this vector. The concept of the length (a.k.a. absolute value or norm) of a vector will be discussed in more detail later on.

Info 10.1.12

The multiplication of a vector by a real number involves the multiplication of each component by this real number. If

\vec{a}

is a vector and

s \in ℝ

, then we have

s \cdot \vec{a} = s \vec{a} = s (\begin{matrix} a_{x} \\ a_{y} \end{matrix}) = (\begin{matrix} s a_{x} \\ s a_{y} \end{matrix})

in the two-dimensional case and

s \cdot \vec{a} = s \vec{a} = s (\begin{matrix} a_{x} \\ a_{y} \\ a_{z} \end{matrix}) = (\begin{matrix} s a_{x} \\ s a_{y} \\ s a_{z} \end{matrix})

in the three-dimensional case. The division of a vector by a number

0 \neq s \in ℝ

is then simply defined as its multiplication by the reciprocal

\frac{1}{s}

\frac{\vec{a}}{s} = \frac{1}{s} \vec{a} .

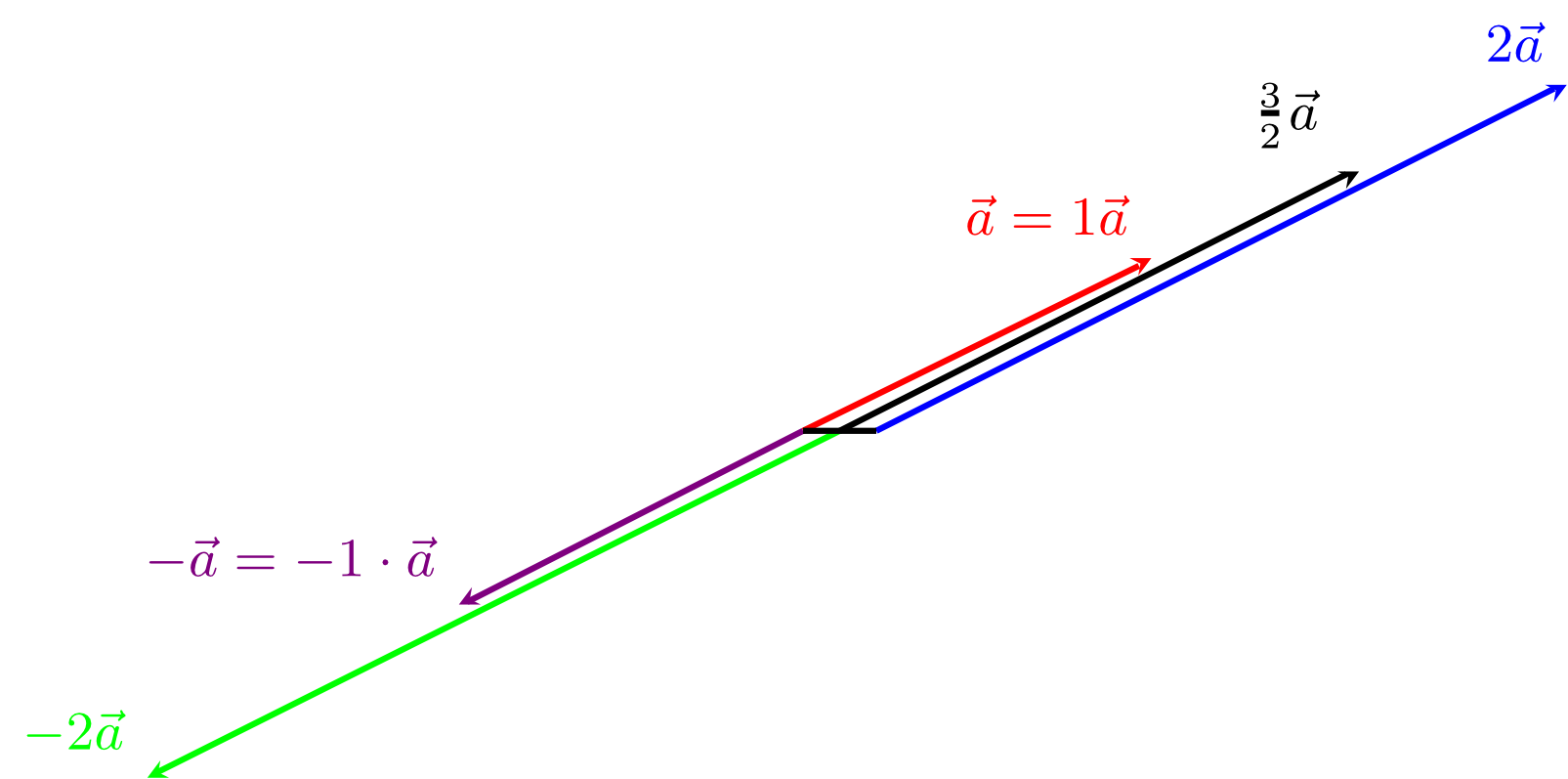
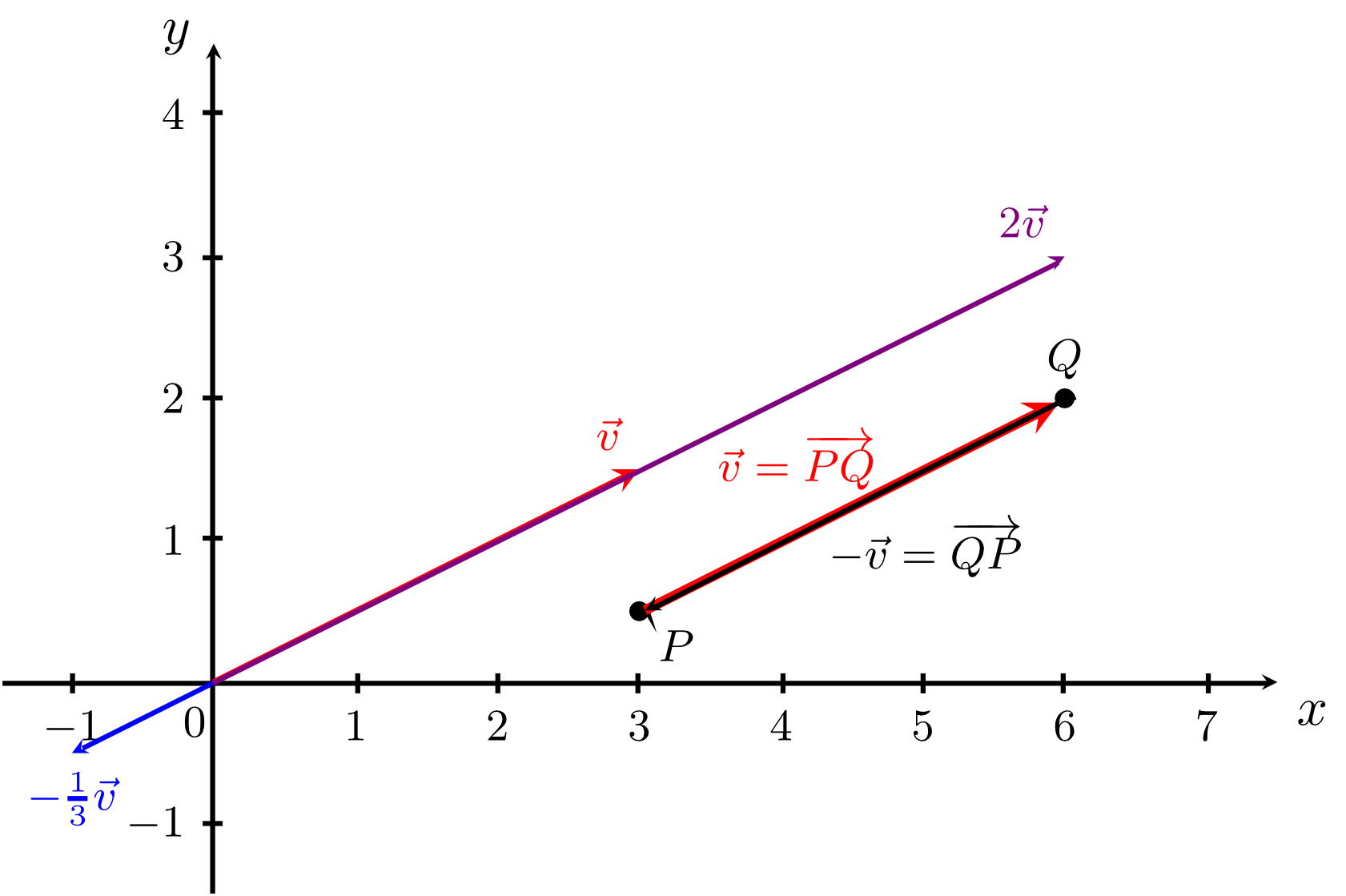
Thus, multiplying a vector by a real number

s \in ℝ

s > 0

results in an equally oriented vector that is stretched by a factor of

s

. For

s \in ℝ

s < 0

, the resulting vector is also stretched by a factor of

s

but it is flipped around by an angle of

π

. In the special case of

s = 0

, we obviously have

0 \vec{a} = \vec{O}

for every vector

\vec{a}

. Two other relevant cases are the multiplication by a factor of

s = 1

1 \cdot \vec{a} = \vec{a}

- which obviously leaves the vector unchanged - and the multiplication by

s = - 1

- 1 \cdot \vec{a} = - \vec{a}

- which results in the so-called opposite vector. This is a vector of equal length and opposite orientation. This is illustrated in the figure below.

Since the multiplication by real numbers changes the length (scales the vectors), real numbers with respect to vectors are often called scalars, and the multiplication of a vector by a real number is called scalar multiplication.

Example 10.1.13

Let the vector

\vec{v} = (\begin{matrix} 3 \\ \frac{3}{2} \end{matrix})

be given. Then, for example, we have

2 \vec{v} = 2 (\begin{matrix} 3 \\ \frac{3}{2} \end{matrix}) = (\begin{matrix} 2 \cdot 3 \\ 2 \cdot \frac{3}{2} \end{matrix}) = (\begin{matrix} 6 \\ 3 \end{matrix})

and

- \frac{\vec{v}}{3} = - \frac{1}{3} \vec{v} = - \frac{1}{3} (\begin{matrix} 3 \\ \frac{3}{2} \end{matrix}) = (\begin{matrix} - 1 \\ - \frac{1}{2} \end{matrix}) .

Moreover,

\vec{v} = \vec{P Q}

for

P = (3; \frac{1}{2})

and

Q = (6; 2)

since

\vec{v} = (\begin{matrix} 3 \\ \frac{3}{2} \end{matrix}) = (\begin{matrix} 6 - 3 \\ 2 - \frac{1}{2} \end{matrix}) .

Then we have

- \vec{v} = - \vec{P Q} = \vec{Q P}

since

- \vec{v} = (\begin{matrix} - 3 \\ - \frac{3}{2} \end{matrix}) = (\begin{matrix} 3 - 6 \\ \frac{1}{2} - 2 \end{matrix}) .

This is illustrated in the figure below.

The following calculation rules apply to scalar multiplication:

Info 10.1.14

Let two real numbers

r

and

s

and two vectors

\vec{a}

and

\vec{b}

be given. Then the following calculation rules apply:

$r \vec{a} = \vec{a} r$
$r s \vec{a} = (r s) \vec{a} = r (s \vec{a})$
$(r + s) \vec{a} = r \vec{a} + s \vec{a}$
$r (\vec{a} + \vec{b}) = r \vec{a} + r \vec{b}$
$r (- \vec{a}) = (- r) \vec{a} = - (r \vec{a})$
$r \vec{a} = 0 \Leftrightarrow r = 0$ or $\vec{a} = \vec{O}$

The first law is called the commutativity law of scalar multiplication, the second is the associativity law of scalar multiplication, and the third and fourth are the distributive laws of scalar multiplication.

Using the concept of an opposite vector we are now able to specify what the subtraction of vectors means.

Info 10.1.15

Let two vectors

\vec{a}

and

\vec{b}

be given. Then, their difference

\vec{a} - \vec{b}

is the sum of

\vec{a}

and the opposite vector of

\vec{b}

. Thus, we have

\vec{a} - \vec{b} = \vec{a} + (- \vec{b}) = (\begin{matrix} a_{x} \\ a_{y} \end{matrix}) + (\begin{matrix} - b_{x} \\ - b_{y} \end{matrix}) = (\begin{matrix} a_{x} - b_{x} \\ a_{y} - b_{y} \end{matrix})

in the two-dimensional case and

\vec{a} - \vec{b} = \vec{a} + (- \vec{b}) = (\begin{matrix} a_{x} \\ a_{y} \\ a_{z} \end{matrix}) + (\begin{matrix} - b_{x} \\ - b_{y} \\ - b_{z} \end{matrix}) = (\begin{matrix} a_{x} - b_{x} \\ a_{y} - b_{y} \\ a_{z} - b_{z} \end{matrix})

in the three-dimensional case. The difference of vectors can also be interpreted geometrically by means of the representatives as illustrated in the figure below.

If we only consider the difference of vectors by means of their components, the question arises what the concept of an opposite vector here is required for. Indeed, the difference of vectors in componentwise notation could also be written analogously to the sum without using the concept of an opposite vector. However, if we think of the geometrical interpretation of the difference by means of representatives (see figure in the Info Box above), we see that a geometrical interpretation is only possible using the concept of an opposite vector.

Example 10.1.16

This example shows typical problems involving the calculation rules for vectors presented so far.

Simplify the following vector expressions:
- $(\begin{matrix} 1 \\ - 2 \\ 0.5 \end{matrix}) - \frac{1}{2} (\begin{matrix} 2 \\ - 3 \\ 1 \end{matrix})$ ,
- $2 (\vec{v} - \vec{w}) + 3 r \vec{w} - r \cdot (- 2 \vec{v})$ für $r \in ℝ$ .
Applying the calculation rules results in
- $(\begin{matrix} 1 \\ - 2 \\ 0.5 \end{matrix}) - \frac{1}{2} (\begin{matrix} 2 \\ - 3 \\ 1 \end{matrix}) = (\begin{matrix} 1 \\ - 2 \\ 0.5 \end{matrix}) - (\begin{matrix} 1 \\ - \frac{3}{2} \\ \frac{1}{2} \end{matrix}) = (\begin{matrix} 1 - 1 \\ - 2 - (- \frac{3}{2}) \\ 0.5 - \frac{1}{2} \end{matrix}) = (\begin{matrix} 0 \\ - \frac{1}{2} \\ 0 \end{matrix}) .$
- $2 (\vec{v} - \vec{w}) + 3 r \vec{w} - r \cdot (- 2 \vec{v}) = 2 \vec{v} - 2 \vec{w} + 3 r \vec{w} + 2 r \vec{v} = 2 (r + 1) \vec{v} + (3 r - 2) \vec{w} .$
Let two vectors $\vec{a} = (\begin{matrix} 1 \\ 2 \end{matrix})$ and $\vec{b} = (\begin{matrix} - 8 \\ 3 \end{matrix})$ be given. Find the unknown vector $\vec{x}$ in the equation

$\vec{a} - 2 \vec{b} - (3 \vec{a} + \vec{x}) = (\begin{matrix} 0 \\ - 1 \end{matrix}) .$

Solving for $\vec{x}$ and substituting $\vec{a}$ and $\vec{b}$ results in

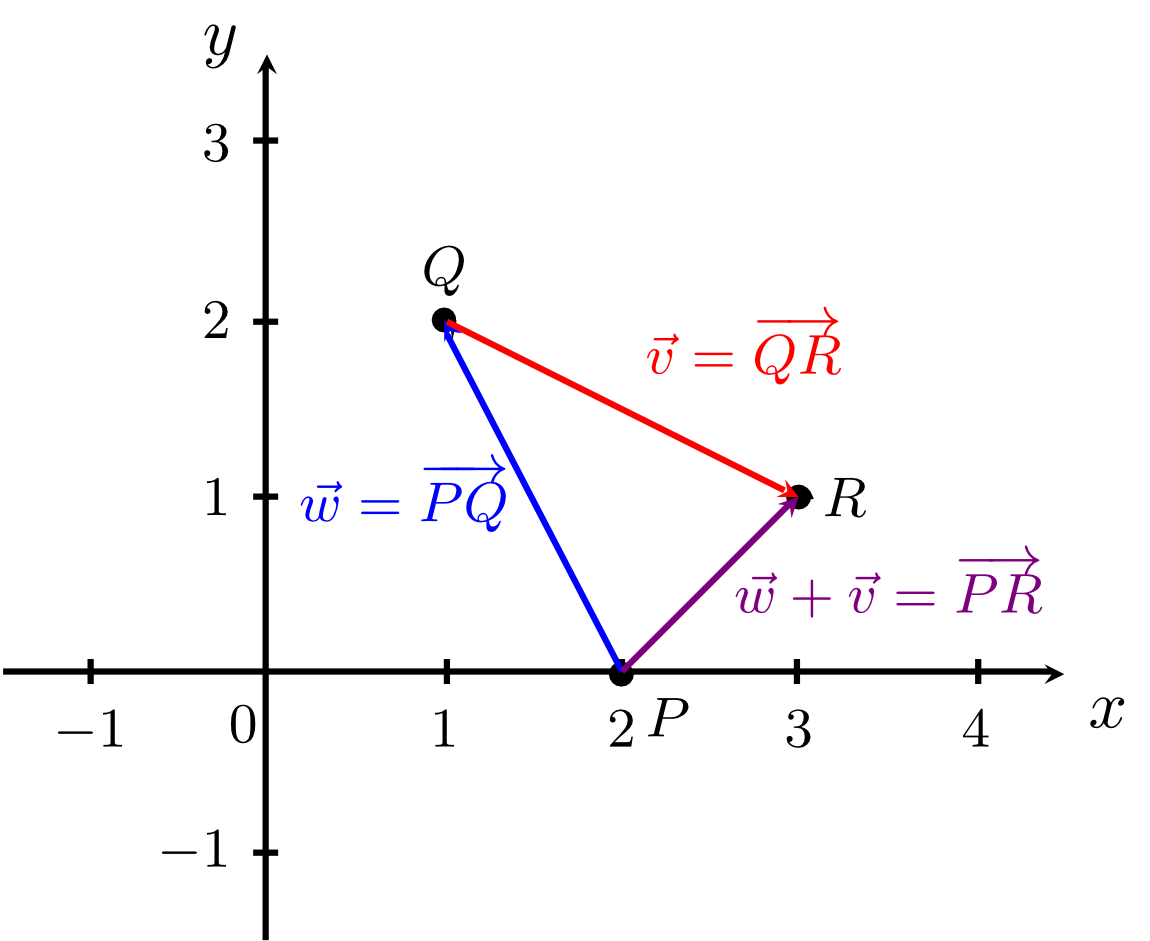
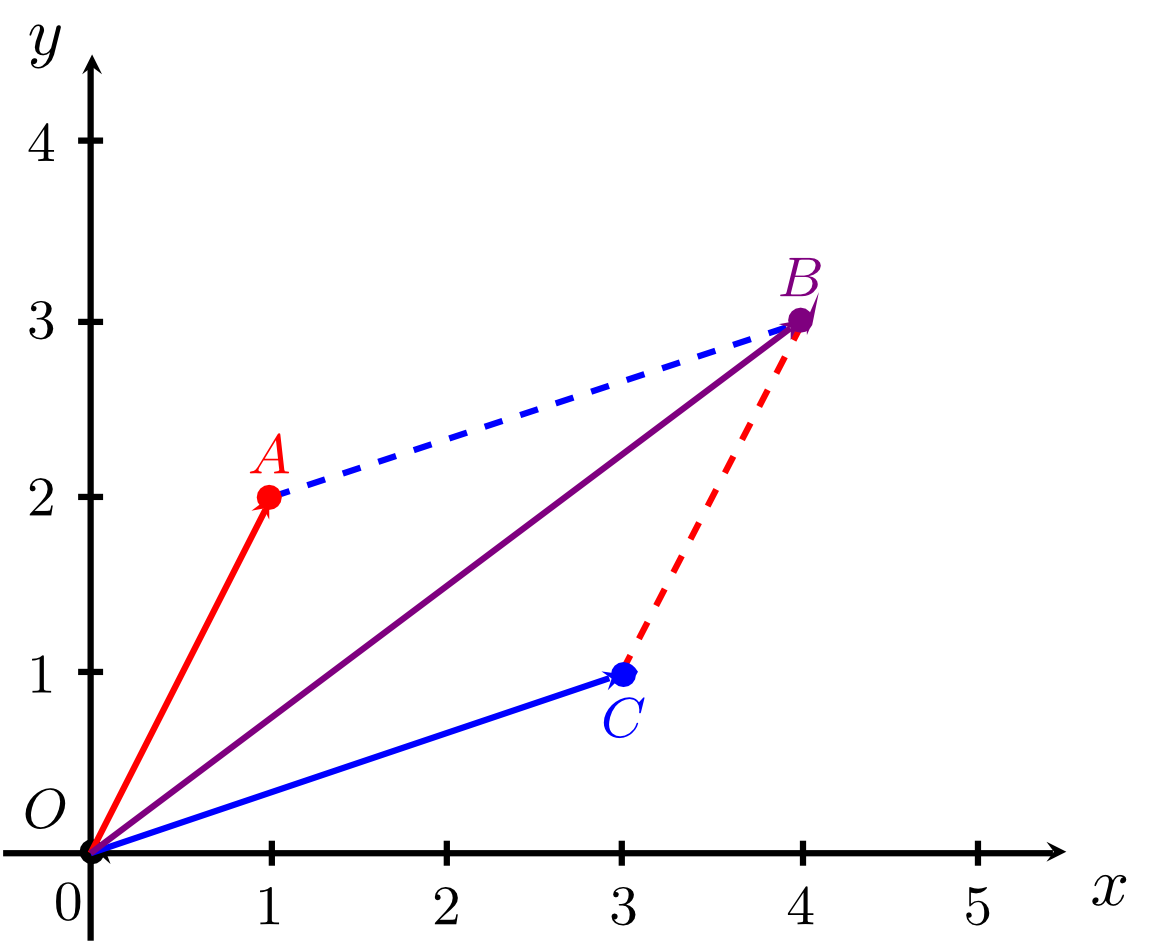
$- (3 \vec{a} + \vec{x}) = (\begin{matrix} 0 \\ - 1 \end{matrix}) - \vec{a} + 2 \vec{b} \Leftrightarrow - \vec{x} = (\begin{matrix} 0 \\ - 1 \end{matrix}) - \vec{a} + 2 \vec{b} + 3 \vec{a} = (\begin{matrix} 0 \\ - 1 \end{matrix}) + 2 (\vec{a} + \vec{b})$

$\Leftrightarrow \vec{x} = - (\begin{matrix} 0 \\ - 1 \end{matrix}) - 2 ((\begin{matrix} 1 \\ 2 \end{matrix}) + (\begin{matrix} - 8 \\ 3 \end{matrix})) = (\begin{matrix} 0 \\ 1 \end{matrix}) - 2 (\begin{matrix} - 7 \\ 5 \end{matrix}) \Leftrightarrow \vec{x} = (\begin{matrix} 14 \\ - 9 \end{matrix}) .$
Using the difference of vectors, specify the connecting vector $\vec{P Q}$ of the two points $P$ and $Q$ by means of the position vectors $\vec{P}$ and $\vec{Q}$ . We have:

$\vec{Q} - \vec{P} = \vec{O Q} - \vec{O P} = - \vec{Q O} - \vec{O P} = - (\vec{Q O} + \vec{O P}) = - \vec{Q P} = \vec{P Q} .$
The connecting vector $\vec{P Q}$ from a point $P$ to a point $Q$ is always the difference of the position vector $\vec{Q}$ (to the terminal point of the connecting vector) and the position vector $\vec{P}$ (to the initial point of the connecting vector). This is illustrated in the figure below and can also be seen from the calculation rule for connecting vectors outlined in Info Box 10.1.5.
The points $A = (2; 1)$ , $B = (4; 2)$ , and $C = (3; 3)$ are the vertices of a triangle. The (geometric) centroid $S$ of this triangle can be calculated by means of the corresponding position vectors:

$\vec{S} = \frac{1}{3} (\vec{A} + \vec{B} + \vec{C}) = \frac{1}{3} ((\begin{matrix} 2 \\ 1 \end{matrix}) + (\begin{matrix} 4 \\ 2 \end{matrix}) + (\begin{matrix} 3 \\ 3 \end{matrix})) = \frac{1}{3} (\begin{matrix} 9 \\ 6 \end{matrix}) = (\begin{matrix} 3 \\ 2 \end{matrix}) .$
Thus, we have $S = (3; 2)$ . This is illustrated in the figure below.

Exercise 10.1.17

Let $P$ , $Q$ , $R$ , and $S$ be points in space. Simplify the expression

$\vec{P Q} - (\vec{P Q} - \vec{Q R}) + \vec{R S}$
as far as possible.
Show that the points $A = (1; 2)$ , $B = (4; 3)$ , and $C = (3; 1)$ together with the origin form the vertices of a parallelogram.

$\vec{P Q} - (\vec{P Q} - \vec{Q R}) + \vec{R S} = \vec{P Q} - \vec{P Q} + \vec{Q R} + \vec{R S} = \vec{O} + \vec{Q R} + \vec{R S} = \vec{Q S} .$
According to the geometrical interpretation of vector addition, the four points form a parallelogram if one of the position vectors $\vec{A}$ , $\vec{B}$ , or $\vec{C}$ is the sum of the two other position vectors. Since we have

$\vec{A} + \vec{C} = (\begin{matrix} 1 \\ 2 \end{matrix}) + (\begin{matrix} 3 \\ 1 \end{matrix}) = (\begin{matrix} 4 \\ 3 \end{matrix}) = \vec{B},$
the three points together with the origin form the vertices of a parallelogram. This is illustrated in the figure below.

Exercise 10.1.18

Simplify the following expressions as far as possible:

$2 (\begin{matrix} - 1 \\ 4 \\ 2 \end{matrix}) - 3 (\begin{matrix} 1 \\ 6 \\ - 2 \end{matrix}) =$ .
$- 2 (\begin{matrix} - t \\ 3 \end{matrix}) - ((\begin{matrix} - 1 \\ 0 \end{matrix}) + \frac{t}{2} (\begin{matrix} 4 \\ - 42 \end{matrix})) =$ .

Vectors can be entered as (a;b) or (a;b;c).

$2 (\begin{matrix} - 1 \\ 4 \\ 2 \end{matrix}) - 3 (\begin{matrix} 1 \\ 6 \\ - 2 \end{matrix}) = (\begin{matrix} - 2 \\ 8 \\ 4 \end{matrix}) - (\begin{matrix} 3 \\ 18 \\ - 6 \end{matrix}) = (\begin{matrix} - 5 \\ - 10 \\ 10 \end{matrix}) .$
$- 2 (\begin{matrix} - t \\ 3 \end{matrix}) - ((\begin{matrix} - 1 \\ 0 \end{matrix}) + \frac{t}{2} (\begin{matrix} 4 \\ - 42 \end{matrix})) = (\begin{matrix} 2 t \\ - 6 \end{matrix}) + (\begin{matrix} 1 \\ 0 \end{matrix}) - (\begin{matrix} 2 t \\ - 21 t \end{matrix}) = (\begin{matrix} 1 \\ 21 t - 6 \end{matrix}) .$

Exercise 10.1.19

Find the vector

\vec{y}

in the equation

3 ((\begin{matrix} 1 \\ - 1 \\ 1 \end{matrix}) - \vec{y}) = - 8 (\begin{matrix} 0.25 \\ 0.25 \\ - 0.25 \end{matrix}) + \vec{y} .

\vec{y} =

3 ((\begin{matrix} 1 \\ - 1 \\ 1 \end{matrix}) - \vec{y}) = - 8 (\begin{matrix} 0.25 \\ 0.25 \\ - 0.25 \end{matrix}) + \vec{y} \Leftrightarrow (\begin{matrix} 3 \\ - 3 \\ 3 \end{matrix}) + 2 (\begin{matrix} 1 \\ 1 \\ - 1 \end{matrix}) = 4 \vec{y}

\Leftrightarrow 4 \vec{y} = (\begin{matrix} 5 \\ - 1 \\ 1 \end{matrix}) \Leftrightarrow \vec{y} = (\begin{matrix} \frac{5}{4} \\ - \frac{1}{4} \\ \frac{1}{4} \end{matrix}) .

Since any vector has an arbitrary number of arrows as its representatives (which arise from each other by parallel translation), all these representatives have the same geometrical length (which is always the distance between the two points they connect). Therefore, it is reasonable to speak of the length of a vector. In mathematics, the length of a vector is called the absolute value or norm.

Info 10.1.20

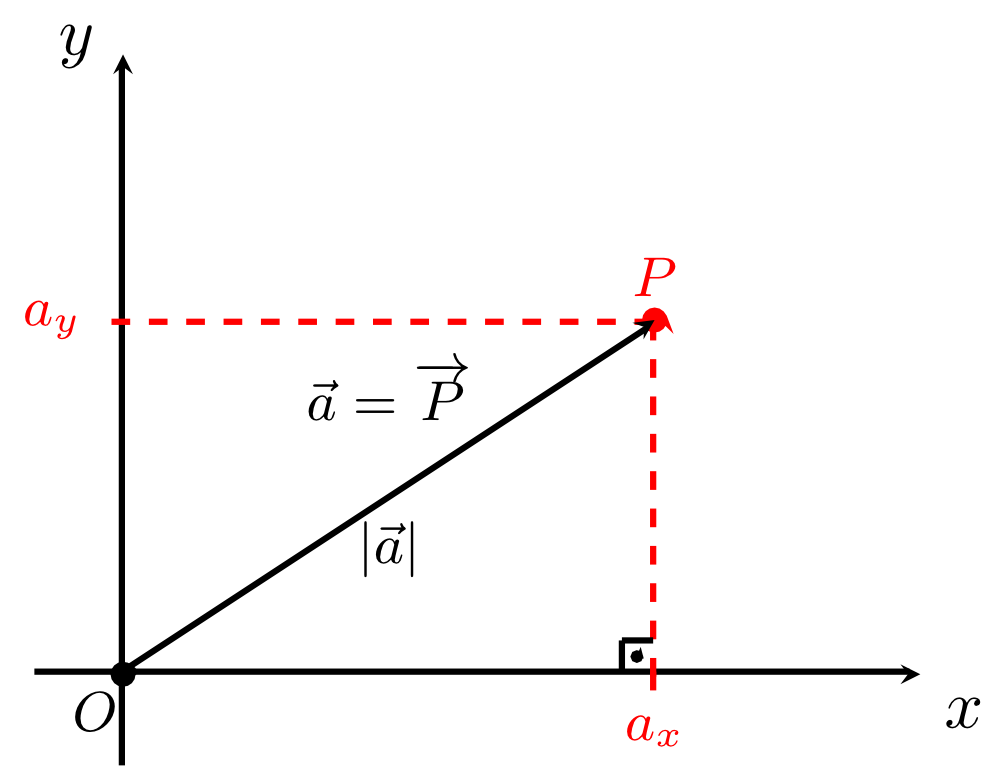
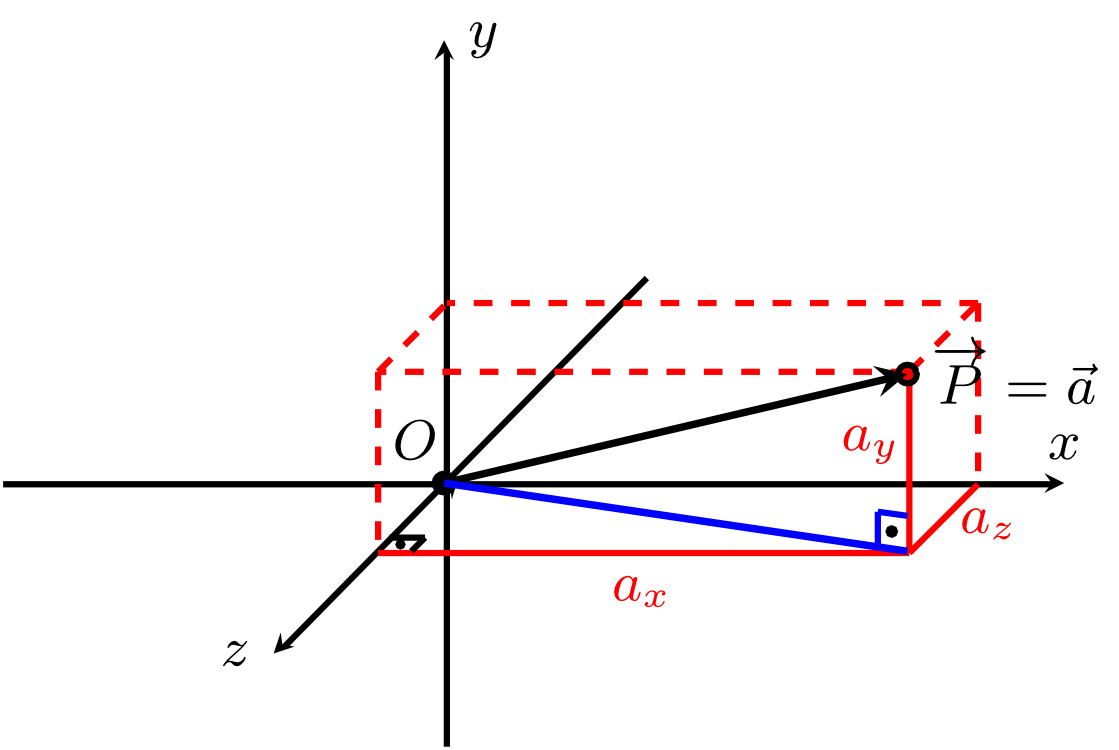
The absolute value or norm of a vector

\vec{a}

is denoted by

| \vec{a} |

and equals the distance between the origin

O

and the point

P

that has the vector

\vec{a}

as its corresponding position vector (i.e.

\vec{P} = \vec{a}

). Thus, we have generally

| \vec{a} | = [\overline{O P}]

and hence in the two-dimensional case

| \vec{a} | = | (\begin{matrix} a_{x} \\ a_{y} \end{matrix}) | = \sqrt{a_{x}^{2} + a_{y}^{2}}

or in the three-dimensional case

| \vec{a} | = | (\begin{matrix} a_{x} \\ a_{y} \\ a_{z} \end{matrix}) | = \sqrt{a_{x}^{2} + a_{y}^{2} + a_{z}^{2}} .

A vector with an absolute value of

1

is also called the unit vector.

Applying the formula given in the Info Box 9.3.2 in Module 9 for the distance of two points in a two-dimensional coordinate system immediately results in the formula for the two-dimensional case:

This is another simple application of Pythagoras' theorem. The three-dimensional case is not much more complex: Pythagoras' theorem can still be applied:

In the figure above two right triangles can be identified. From the right triangle lying in the

xz

-plane we obtain

\sqrt{a_{x}^{2} + a_{z}^{2}}

for the length of the blue line. From the second right triangle we then obtain for the length of the segment from

O

P

, i.e. for

| \vec{a} |

\sqrt{a_{y}^{2} + {(\sqrt{a_{x}^{2} + a_{z}^{2}})}^{2}} = \sqrt{a_{x}^{2} + a_{y}^{2} + a_{z}^{2}} .

For norms of vectors the following calculation rules apply:

Info 10.1.21

Let two vectors

\vec{a}

and

\vec{b}

(both in

ℝ^{2}

or in

ℝ^{3}

) and a real number

r \in ℝ

be given. Then, we have:

$| \vec{a} | \geq 0$ and $| \vec{a} | = 0 \Leftrightarrow \vec{a} = \vec{O}$ ,
$| r \vec{a} | = | r | \cdot | \vec{a} |$ , and
$| \vec{a} + \vec{b} | \leq | \vec{a} | + | \vec{b} |$ .

The first rule states that norms are always non-negative and that only the norm of the zero vector is

0

. The second rule is especially useful in calculating the norms of constant multiples of vectors. The third rule is called the triangle inequality.

Example 10.1.22

The absolute value of the vector $\frac{1}{4} (\begin{matrix} 3 \\ - 1 \\ \sqrt{6} \end{matrix})$ is

$| \frac{1}{4} (\begin{matrix} 3 \\ - 1 \\ \sqrt{6} \end{matrix}) | = | \frac{1}{4} | | (\begin{matrix} 3 \\ - 1 \\ \sqrt{6} \end{matrix}) | = \frac{1}{4} \sqrt{3^{2} + (- 1)^{2} + 6} = \frac{\sqrt{16}}{4} = 1 .$
Hence, this is a unit vector.
Find a number $q \in ℝ$ such that $| (\begin{matrix} q^{2} - 2 \\ 4 \end{matrix}) - 2 (\begin{matrix} q - 1 \\ q \end{matrix}) | = 0$ .

$| (\begin{matrix} q^{2} - 2 \\ 4 \end{matrix}) - 2 (\begin{matrix} q - 1 \\ q \end{matrix}) | = | (\begin{matrix} q^{2} - 2 q \\ 4 - 2 q \end{matrix}) | = 0 \Leftrightarrow (\begin{matrix} q^{2} - 2 q \\ 4 - 2 q \end{matrix}) = (\begin{matrix} 0 \\ 0 \end{matrix})$

$\Leftrightarrow q^{2} - 2 q = 0 and 4 - 2 q = 0 \Leftrightarrow q (q - 2) = 0 and 2 (2 - q) = 0 \Leftrightarrow q = 2 .$

Exercise 10.1.23

Calculate

| - \frac{1}{3} (\begin{matrix} 2 \\ - 14 \\ 5 \end{matrix}) | =

| - \frac{1}{3} (\begin{matrix} 2 \\ - 14 \\ 5 \end{matrix}) | = | - \frac{1}{3} | \cdot | (\begin{matrix} 2 \\ - 14 \\ 5 \end{matrix}) | = \frac{1}{3} \sqrt{2^{2} + (- 14)^{2} + 5^{2}} = \frac{1}{3} \sqrt{225} = \frac{15}{3} = 5 .

Exercise 10.1.24

Find the number

χ > 3

such that

| (\begin{matrix} 3 \\ χ \end{matrix}) - (\begin{matrix} χ \\ 3 \end{matrix}) | = 2 \sqrt{2}

χ =

| (\begin{matrix} 3 \\ χ \end{matrix}) - (\begin{matrix} χ \\ 3 \end{matrix}) | = | (\begin{matrix} 3 - χ \\ χ - 3 \end{matrix}) | = \sqrt{(3 - χ)^{2} + (χ - 3)^{2}} = 2 \sqrt{2} \Leftrightarrow \sqrt{2 (3 - χ)^{2}} = 2 \sqrt{2}

\Leftrightarrow | 3 - χ | = 2 \Leftrightarrow χ = 1 or χ = 5 .

From

χ > 3

, it follows that

χ = 5

Exercise 10.1.25

Show that the points

A = (4; 2; 7)

B = (3; 1; 9)

, and

C = (2; 3; 8)

are the vertices of an equilateral triangle.

The triangle is equilateral if

| \vec{A B} | = | \vec{A C} | = | \vec{B C} | .

| \vec{A B} | = | \vec{B} - \vec{A} | = | (\begin{matrix} 3 \\ 1 \\ 9 \end{matrix}) - (\begin{matrix} 4 \\ 2 \\ 7 \end{matrix}) | = | (\begin{matrix} - 1 \\ - 1 \\ 2 \end{matrix}) | = \sqrt{(- 1)^{2} + (- 1)^{2} + 2^{2}} = \sqrt{6},

| \vec{A C} | = | \vec{C} - \vec{A} | = | (\begin{matrix} 2 \\ 3 \\ 8 \end{matrix}) - (\begin{matrix} 4 \\ 2 \\ 7 \end{matrix}) | = | (\begin{matrix} - 2 \\ 1 \\ 1 \end{matrix}) | = \sqrt{(- 2)^{2} + 1^{2} + 1^{2}} = \sqrt{6},

| \vec{B C} | = | \vec{C} - \vec{B} | = | (\begin{matrix} 2 \\ 3 \\ 8 \end{matrix}) - (\begin{matrix} 3 \\ 1 \\ 9 \end{matrix}) | = | (\begin{matrix} - 1 \\ 2 \\ - 1 \end{matrix}) | = \sqrt{(- 1)^{2} + 2^{2} + (- 1)^{2}} = \sqrt{6} .

Thus, the triangle is equilateral.

Onlinebrückenkurs Mathematik

1. Elementary Arithmetic

2. Equations in one Variable

3. Inequalities in one Variable

4. System of Linear Equations

5. Geometry

6. Elementary Functions

7. Differential Calculus

8. Integral Calculus

9. Objects in the Two-Dimensional Coordinate System

10. Basic Concepts of Descriptive Vector Geometry

11. Language of Descriptive Statistics

Chapter 10 Basic Concepts of Descriptive Vector Geometry

10.1.4 Simple Vector Operations

Info 10.1.8

Info 10.1.9

Example 10.1.10

Exercise 10.1.11

Info 10.1.12

Example 10.1.13

Info 10.1.14

Info 10.1.15

Example 10.1.16

Exercise 10.1.17

Exercise 10.1.18

Exercise 10.1.19

Info 10.1.20

Info 10.1.21

Example 10.1.22

Exercise 10.1.23

Exercise 10.1.24

Exercise 10.1.25

		$\vec{P} + (\vec{P Q} + \vec{Q R})$
		$\vec{P R}$
		$\vec{Q R}$
		$\vec{O R}$
		$\vec{R}$
		$\vec{Q} + \vec{Q R}$