Chapter 10 Basic Concepts of Descriptive Vector Geometry

Section 10.2 Lines and Planes

10.2.2 Lines in the Plane and in Space

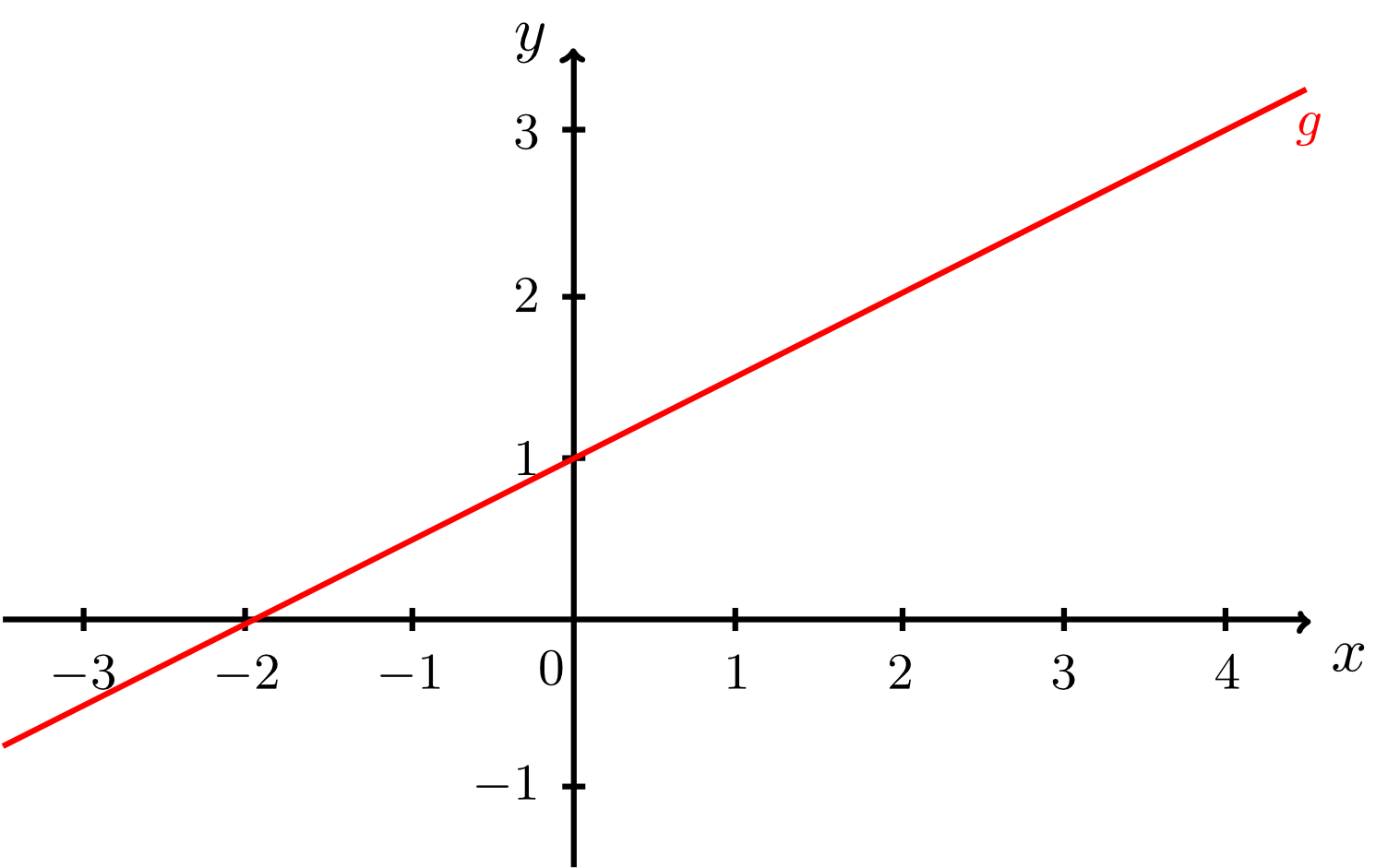
In Module 9 we described lines in the plane using coordinate equations for the points lying on the lines with respect to a fixed coordinate system. In this way, for example, a line

g

with slope

\frac{1}{2}

and

y

-intercept

1

is given as the set of points

g = {(x; y) \in ℝ^{2} : y = \frac{1}{2} x + 1},

which is often abbreviated by specifying only the coordinate equation of a line (here in normal form):

g : y = \frac{1}{2} x + 1 .

The figure below shows this line.

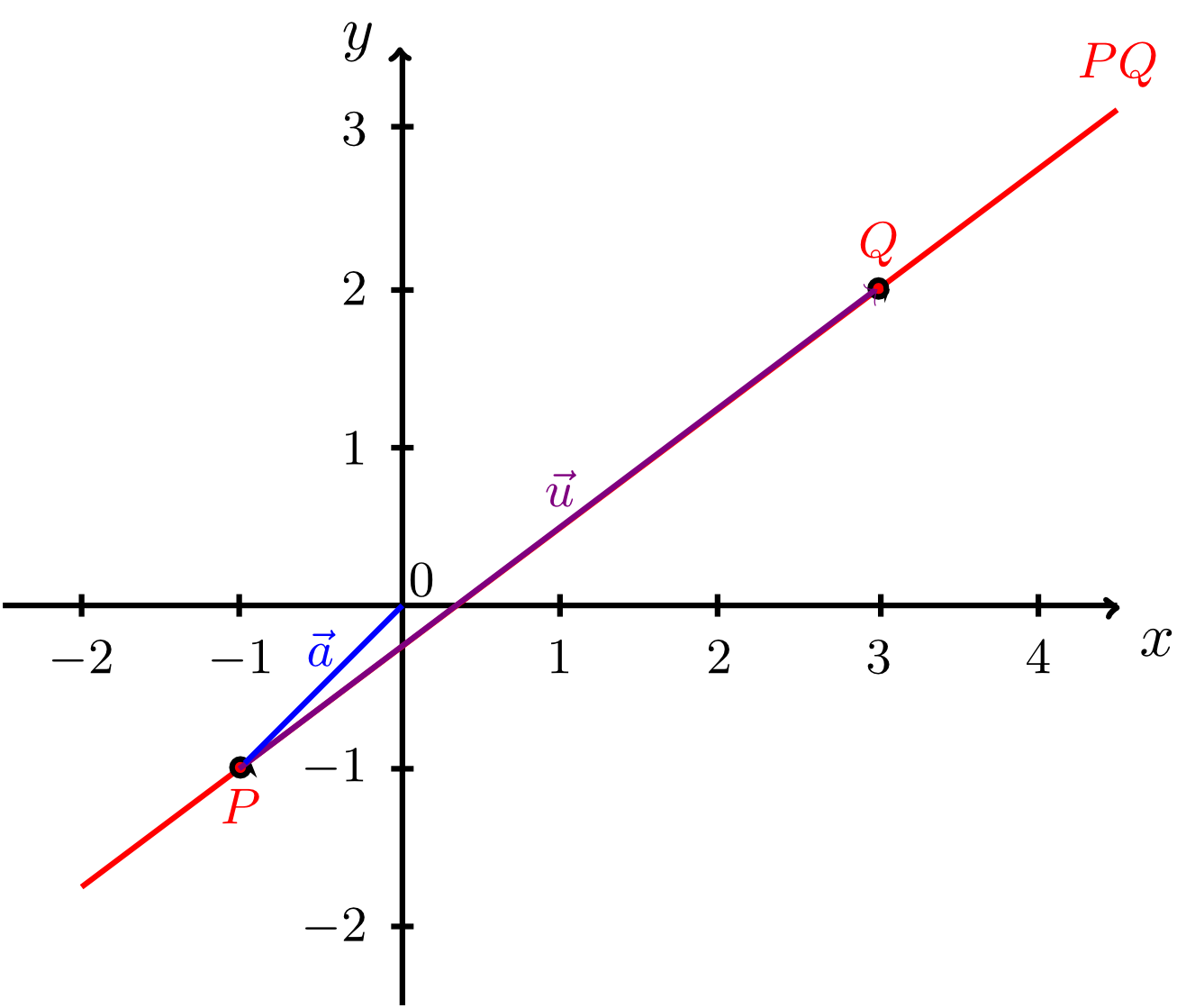
In the following sections we want to describe the points on the line by only their corresponding position vectors. The considerations outlined below result in the following description: the coordinates of the points

(x; y)

lying on the line

g

satisfy the equation

y = \frac{1}{2} x + 1 .

This equation can be substituted into the description of the point. Then, we see that the line

g

consists of points of the form

(x; \frac{1}{2} x + 1)

with

x \in ℝ

. Let the corresponding position vectors of these points be denoted by

\vec{r}

. Then, we have

\vec{r} = (\begin{matrix} x \\ \frac{1}{2} x + 1 \end{matrix}) = x (\begin{matrix} 1 \\ \frac{1}{2} \end{matrix}) + (\begin{matrix} 0 \\ 1 \end{matrix})

with

x \in ℝ

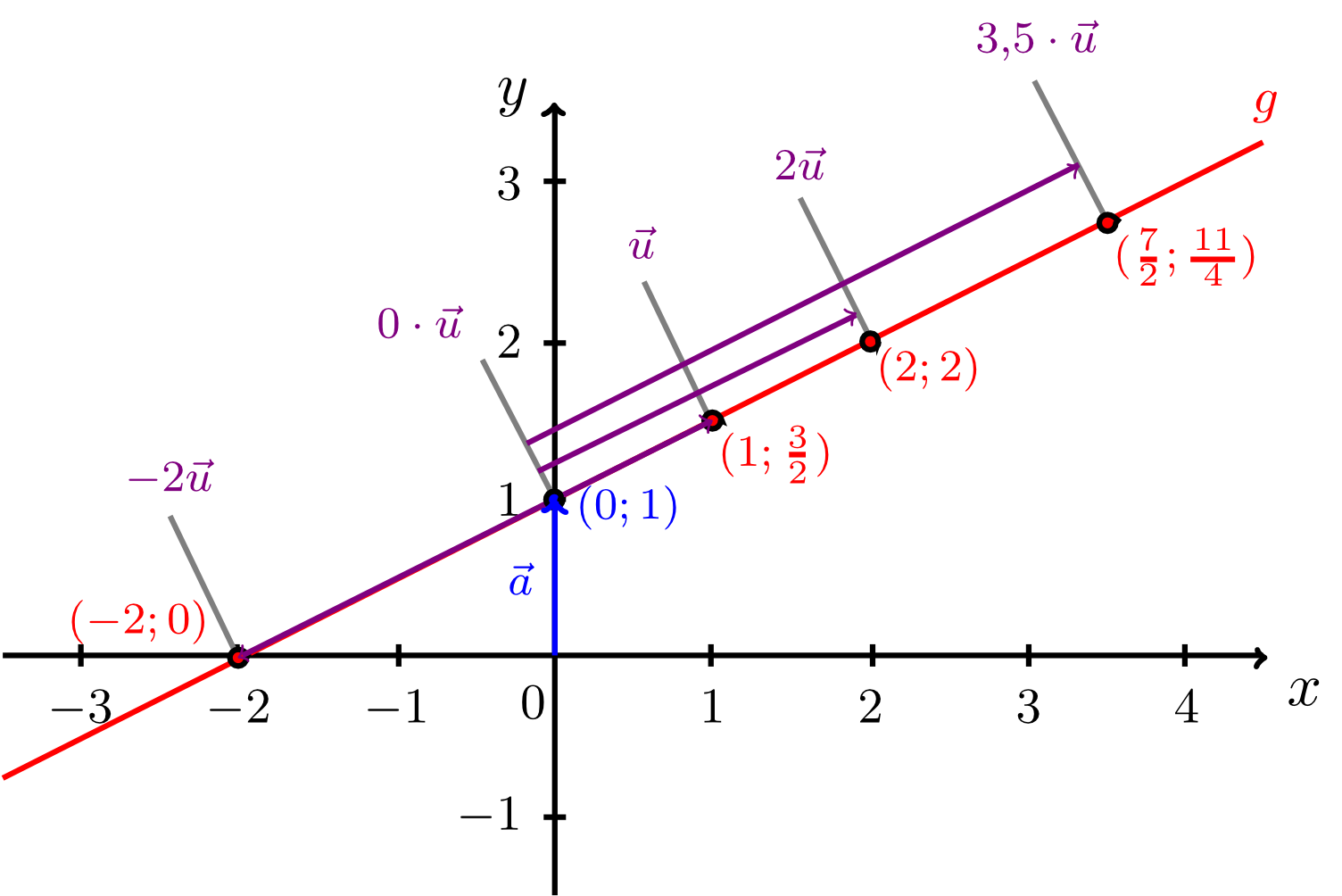
. Using position vectors, the line

g

can also be described by

g : \vec{r} = x (\begin{matrix} 1 \\ \frac{1}{2} \end{matrix}) + (\begin{matrix} 0 \\ 1 \end{matrix}), x \in ℝ .

In other words: The points of

g

are defined by the sum of the vector

\vec{a} = (\begin{matrix} 0 \\ 1 \end{matrix})

and all possible multiples of the vector

\vec{u} = (\begin{matrix} 1 \\ \frac{1}{2} \end{matrix})

, i.e. all vectors collinear to the vector

(\begin{matrix} 1 \\ \frac{1}{2} \end{matrix})

. The figure below illustrates this approach.

The Info Box below outlines the most relevant terms, methods and concepts for this so-called vector form or parametric form of an equation of a line.

Info 10.2.2

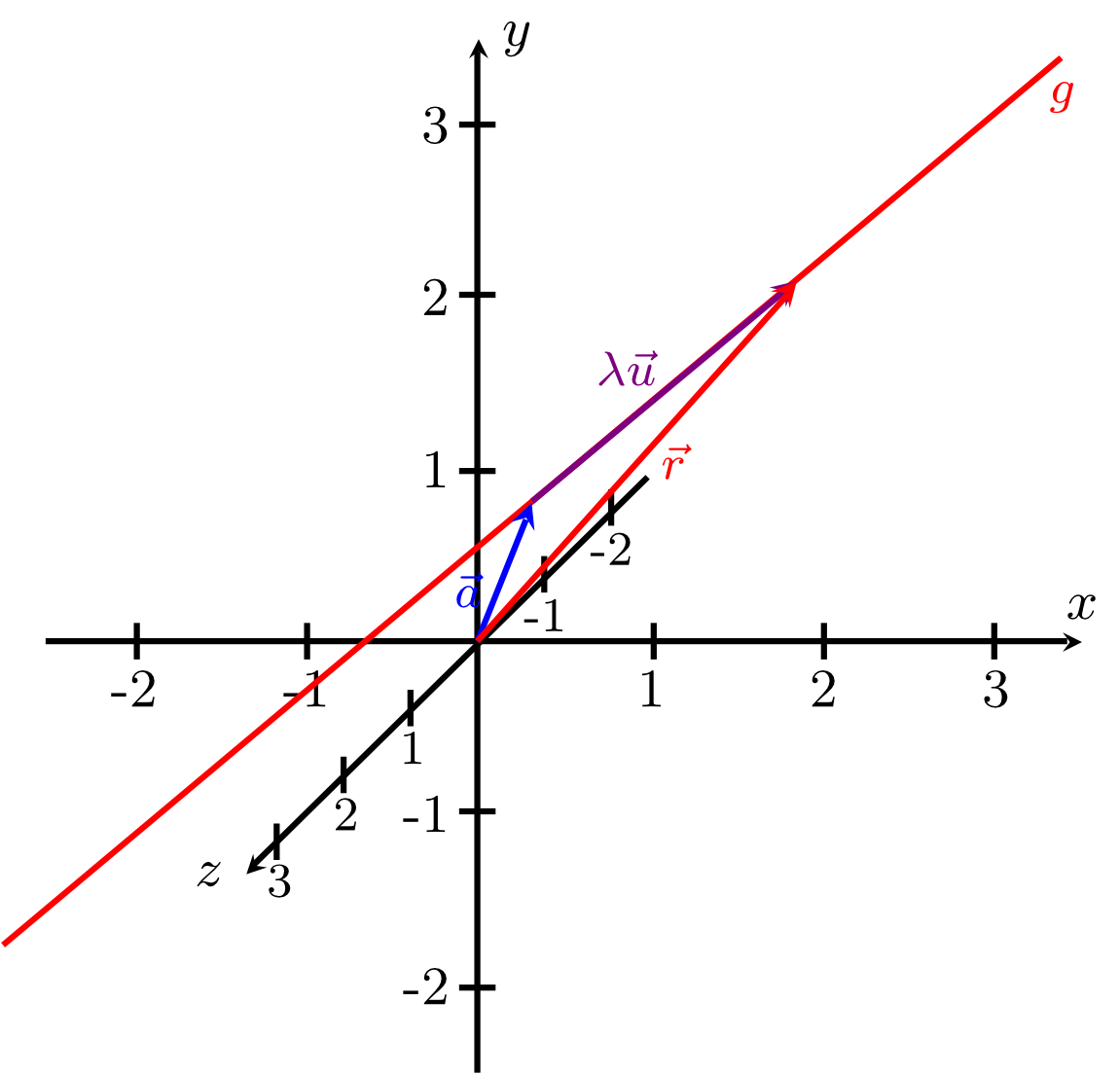
A line $g$ in the plane is given in vector form or in parametric form as the set of position vectors

$g = {\vec{r} = λ \vec{u} + \vec{a} \in ℝ^{2} : λ \in ℝ},$
often written in short as

$g : \vec{r} = λ \vec{u} + \vec{a}, λ \in ℝ .$
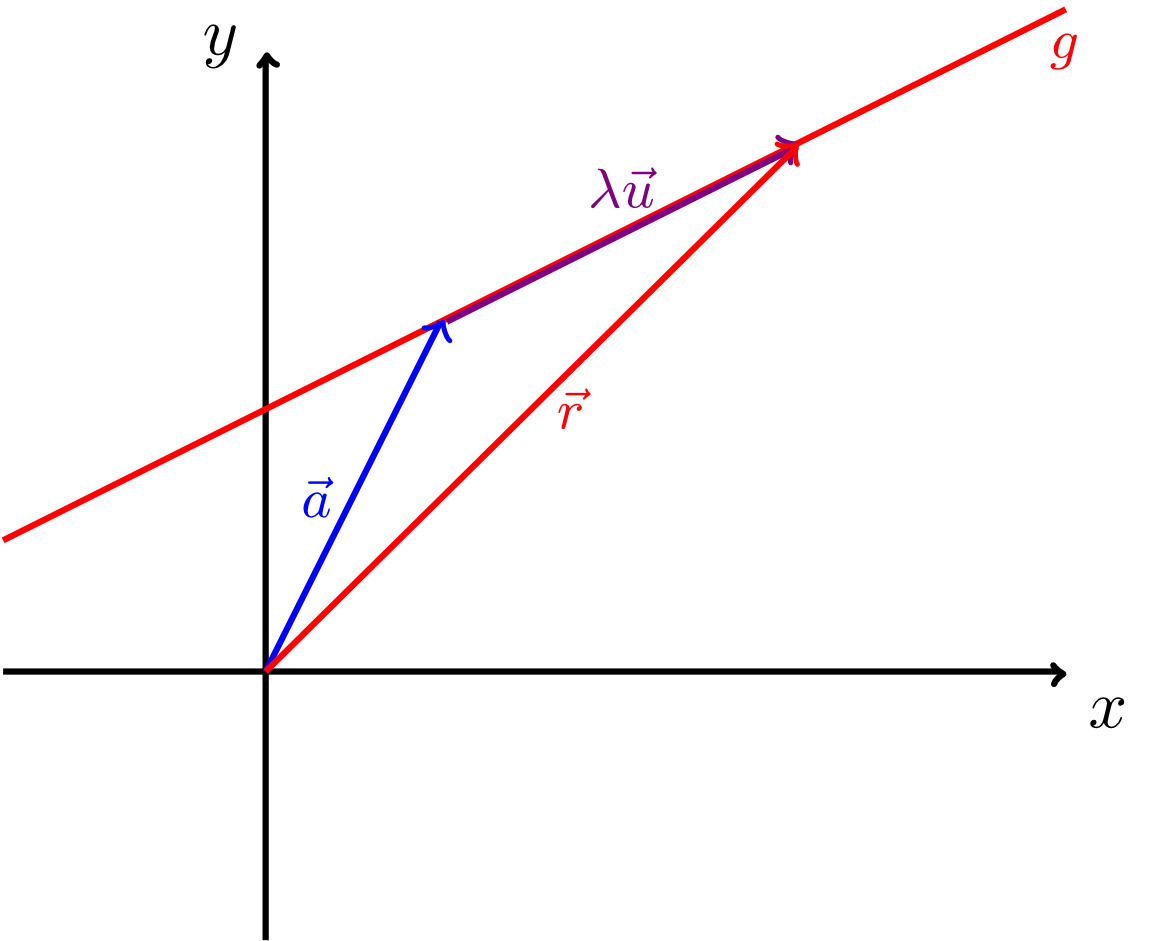
Here, $λ$ is called a parameter, $\vec{a}$ is called the reference vector, and $\vec{u} \neq \vec{O}$ is called he direction vector of the line. The position vectors $\vec{r}$ point to the individual points on the line. The reference vector $\vec{a}$ is the position vector of a fixed point on the line that is called a reference point. The multiples $λ \vec{u}$ of the direction vector $\vec{u}$ are all vectors collinear to $\vec{u}$ (see figure below).
For a line $g$ given in normal form by the equation

$g : y = m x + b$
the vector form of the equation of a line can be found by generating the position vectors $(\begin{matrix} x \\ m x + b \end{matrix}) = x (\begin{matrix} 1 \\ m \end{matrix}) + (\begin{matrix} 0 \\ b \end{matrix})$ . Then, the vector form of the equation of a line is

$g : \vec{r} = x (\begin{matrix} 1 \\ m \end{matrix}) + (\begin{matrix} 0 \\ b \end{matrix}), x \in ℝ$
with the direction vector $\vec{u} = (\begin{matrix} 1 \\ m \end{matrix})$ and the reference vector $\vec{a} = (\begin{matrix} 0 \\ b \end{matrix})$ .
For a line $g$ given by the equation in parametric form:

$g : \vec{r} = λ \vec{u} + \vec{a}, λ \in ℝ$
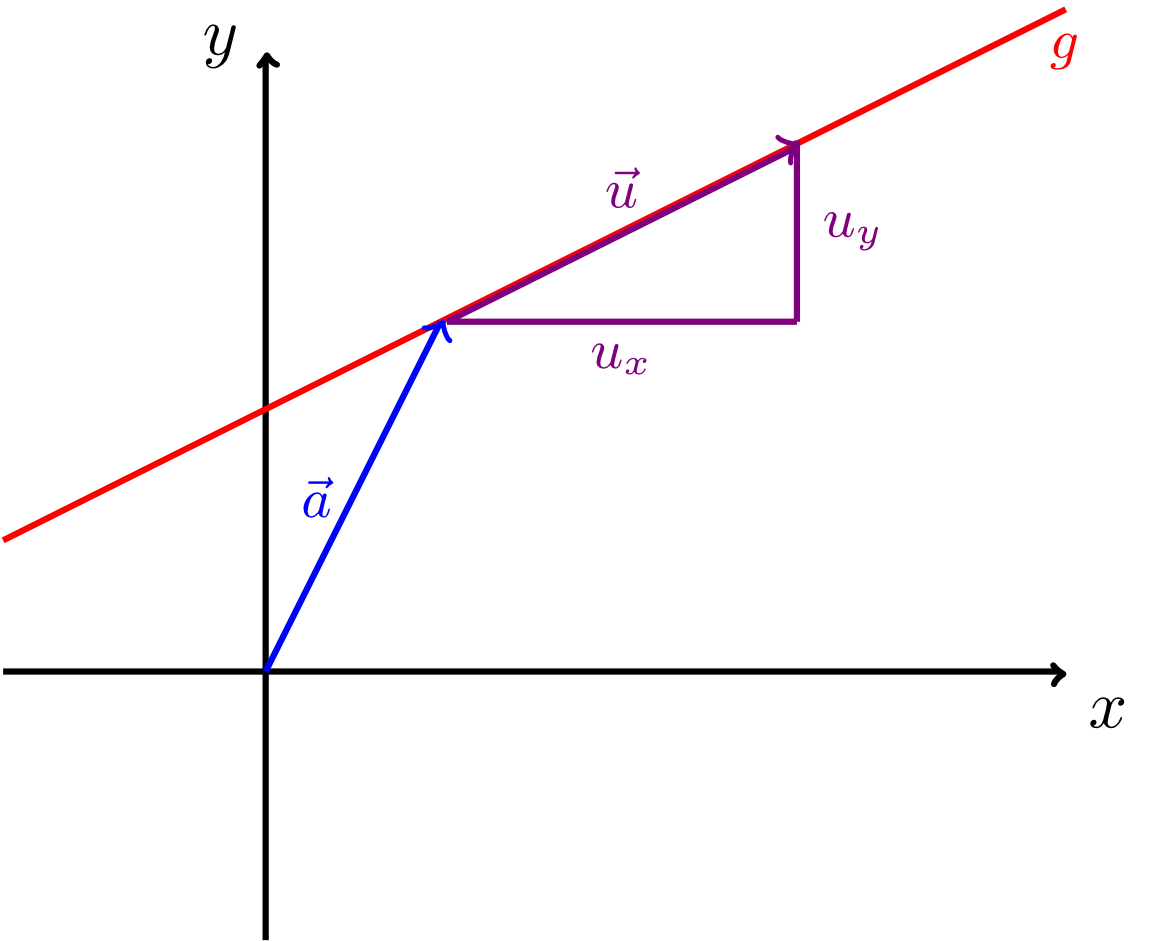
the corresponding equation of the line can be found as follows: the direction vector $\vec{u} = (\begin{matrix} u_{x} \\ u_{y} \end{matrix})$ immediately provides the slope of the line via a slope triangle. We have

$m = \frac{u_{y}}{u_{x}} .$

(Here, $u_{x}$ must be non-zero, i.e. $u_{x} \neq 0$ . The special case $u_{x} = 0$ is discussed in the example below.) From Section 9.2.2 we know that we only need another point on the line to determine the $y$ -intercept $b$ and specify the equation of the line in normal form. It is easiest to use the reference point $\vec{a}$ for this.

One can immediately see that the parametric form of the equation of a line is not unique. Every point on the line can be used as reference point, and the direction vector can be chosen from an arbitrary number of collinear vectors. For example, the line

g

with the equation of a line

g : \frac{1}{2} x + 1

in coordinate form discussed in the first example of the subsection is not only described by the vector equation

g : \vec{r} = x (\begin{matrix} 1 \\ \frac{1}{2} \end{matrix}) + (\begin{matrix} 0 \\ 1 \end{matrix}), x \in ℝ

in parametric form, but also by the equations

g : \vec{r} = λ (\begin{matrix} 2 \\ 1 \end{matrix}) + (\begin{matrix} 2 \\ 2 \end{matrix}), λ \in ℝ

g : \vec{r} = ν (\begin{matrix} - 2 \\ - 1 \end{matrix}) + (\begin{matrix} - 2 \\ 0 \end{matrix}), ν \in ℝ .

Often representations are chosen such that the direction vector is as simple as possible. However, for representations of the same line by different direction vectors or reference vectors, different parameter values have to be used since in different representations the same parameter value defines different points on the line. For example, the parameter value

λ = 1

defines, in the corresponding parametric equation of

g

, the point

1 \cdot (\begin{matrix} 2 \\ 1 \end{matrix}) + (\begin{matrix} 2 \\ 2 \end{matrix}) = (\begin{matrix} 4 \\ 3 \end{matrix}),

but the parameter value

ν = 1

defines, in the corresponding parametric equation of

g

, the point

1 \cdot (\begin{matrix} - 2 \\ - 1 \end{matrix}) + (\begin{matrix} - 2 \\ 0 \end{matrix}) = (\begin{matrix} - 4 \\ - 1 \end{matrix}) .

The example below lists a few applications of equations of a line in vector form.

Example 10.2.3

Let the line $g$ in the plane be given by the equation

$g : 2 y - 3 x = 6 .$
Find two different equations of a line of $g$ in vector form.
First, we transform the equation of a line into normal form:

$2 y - 3 x = 6 \Leftrightarrow y = \frac{3}{2} x + 3 .$
Thus, points on the line $g$ have the form $(x; \frac{3}{2} x + 3)$ , $x \in ℝ$ described by the position vector $(\begin{matrix} x \\ \frac{3}{2} x + 3 \end{matrix})$ , $x \in ℝ$ . Hence, one possible parametric form is given by

$g : \vec{r} = x (\begin{matrix} 1 \\ \frac{3}{2} \end{matrix}) + (\begin{matrix} 0 \\ 3 \end{matrix}), x \in ℝ .$
Choosing another direction vector collinear to $(\begin{matrix} 1 \\ \frac{3}{2} \end{matrix})$ and another reference point on $g$ results in another equation of a line in parametric form. For example, $(\begin{matrix} 2 \\ 3 \end{matrix})$ is collinear to $(\begin{matrix} 1 \\ \frac{3}{2} \end{matrix})$ since $(\begin{matrix} 2 \\ 3 \end{matrix}) = 2 (\begin{matrix} 1 \\ \frac{3}{2} \end{matrix})$ . $(\begin{matrix} 2 \\ 6 \end{matrix})$ is another appropriate reference vector since the coordinates of the point $(2; 6)$ obviously satisfy the equation of a line. Hence,

$g : \vec{r} = σ (\begin{matrix} 2 \\ 3 \end{matrix}) + (\begin{matrix} 2 \\ 6 \end{matrix}), σ \in ℝ$
is another possible parametric form of an equation of the line $g$ .
In the case of a line with an equation that cannot be transformed into normal form, such as

$h : x = 2,$
an equation in parametric form can still be given.
All points on the line $h$ have the form $(2; y)$ for $y \in ℝ$ , with the corresponding position vector $(\begin{matrix} 2 \\ y \end{matrix})$ for $y \in ℝ$ . Since $(\begin{matrix} 2 \\ y \end{matrix}) = y (\begin{matrix} 0 \\ 1 \end{matrix}) + (\begin{matrix} 2 \\ 0 \end{matrix})$ , one possible vector form of $h$ is given by

$h : \vec{r} = y (\begin{matrix} 0 \\ 1 \end{matrix}) + (\begin{matrix} 2 \\ 0 \end{matrix}), y \in ℝ .$
Let the line $α$ be given in parametric form by

$α : \vec{r} = μ (\begin{matrix} - 3 \\ 2 \end{matrix}) + (\begin{matrix} 1 \\ 1 \end{matrix}), μ \in ℝ .$
Find the corresponding equation of a line in normal form.
The direction vector $(\begin{matrix} - 3 \\ 2 \end{matrix})$ gives the slope $m = \frac{2}{- 3} = - \frac{2}{3}$ . Thus, the equation of the line in normal form is

$α : y = - \frac{2}{3} x + b .$
The reference vector of $α$ is $(\begin{matrix} 1 \\ 1 \end{matrix})$ . The reference point $(1; 1)$ can be substituted into the equation of the line to determine the $y$ -intercept:

$1 = - \frac{2}{3} \cdot 1 + b \Leftrightarrow b = \frac{5}{3} .$
Thus, we have

$α : y = - \frac{2}{3} x + \frac{5}{3} .$
If, for example, a line is given by the equation

$β : \vec{r} = λ (\begin{matrix} 0 \\ - 2 \end{matrix}) + (\begin{matrix} - 1 \\ 1 \end{matrix}), λ \in ℝ$
in parametric form, where the $x$ -component of the direction vector is $0$ , the corresponding equation of the line in component form can be found.
The direction vector with an $x$ -component of $0$ implies that the line is parallel to the $y$ -axis. Hence, the equation of the line has the form

$β : x = c .$
The constant $c$ can be determined by substituting the reference point $(- 1; 1)$ into this equation resulting in $- 1 = c$ , and we get

$β : x = - 1 .$
Given the two points $P = (- 1; - 1)$ and $Q = (3; 2)$ , find the equation of a line of $P Q$ in parametric form.
For the direction vector we the connection vector

$\vec{u} = \vec{P Q} = \vec{Q} - \vec{P} = (\begin{matrix} 3 \\ 2 \end{matrix}) - (\begin{matrix} - 1 \\ - 1 \end{matrix}) = (\begin{matrix} 4 \\ 3 \end{matrix})$
and for the reference vector we use the position vector of a given point, for example,

$\vec{a} = \vec{P} = (\begin{matrix} - 1 \\ - 1 \end{matrix}) .$
Thus, we have

$P Q : \vec{r} = λ (\begin{matrix} 4 \\ 3 \end{matrix}) + (\begin{matrix} - 1 \\ - 1 \end{matrix}), λ \in ℝ .$
The line is shown in the figure below.

Exercise 10.2.4

Let the line $g$ be given by the equation

$g : \vec{r} = t (\begin{matrix} - 1 \\ 5 \end{matrix}) + (\begin{matrix} 2 \\ 5 \end{matrix}), t \in ℝ$
in parametric form. Find the equation $g$ in normal form:
$g : y =$ .
The line $h$ with the equation of a line in coordinate form

$h : \frac{1}{2} y + x + 2 = 0$
has the parametric form

$h : \vec{r} = s (\begin{matrix} a \\ 2 \end{matrix}) + (\begin{matrix} b \\ - 5 \end{matrix}), s \in ℝ .$
Find the missing values of $a$ and $b$ .
$a =$

$b =$

Consider the two points

A = (- 2; - 1)

and

B = (3; - \frac{3}{2})

. Which of the following parametric equations are correct representations of the line

A B

	(i)	$A B : \vec{r} = s (\begin{matrix} 5 \\ - \frac{1}{2} \end{matrix}) + (\begin{matrix} 0 \\ - \frac{6}{5} \end{matrix}), s \in ℝ$
	(ii)	$A B : \vec{r} = t (\begin{matrix} 5 \\ \frac{1}{2} \end{matrix}) + (\begin{matrix} - 2 \\ - 1 \end{matrix}), t \in ℝ$
	(iii)	$A B : \vec{r} = u (\begin{matrix} - 5 \\ \frac{1}{2} \end{matrix}) + (\begin{matrix} - 12 \\ 0 \end{matrix}), u \in ℝ$
	(iv)	$A B : \vec{r} = v (\begin{matrix} 10 \\ - 1 \end{matrix}) + (\begin{matrix} 4 \\ - \frac{8}{5} \end{matrix}), v \in ℝ$
	(v)	$A B : \vec{r} = w (\begin{matrix} - 1 \\ 10 \end{matrix}) + (\begin{matrix} - 22 \\ 1 \end{matrix}), w \in ℝ$
	(vi)	$A B : \vec{r} = z (\begin{matrix} \frac{5}{2} \\ - \frac{1}{4} \end{matrix}) + (\begin{matrix} \frac{6}{5} \\ - 1 \end{matrix}), z \in ℝ$

Find the value of $ψ$ such that the point $P$ with the position vector

$\vec{P} = (\begin{matrix} - 2 \\ ψ \end{matrix})$
lies on the line

$i : \vec{r} = τ (\begin{matrix} 1 \\ - 3 \end{matrix}) + (\begin{matrix} - 1 \\ 2 \end{matrix}), τ \in ℝ,$
and find the value of the parameter $τ$ such that $\vec{r} = \vec{P}$ .
$ψ =$

$τ =$

The slope of the line can be found from the direction vector $(\begin{matrix} - 1 \\ 5 \end{matrix})$ : $m = \frac{5}{- 1} = - 5$ . Thus, we have

$g : y = - 5 x + b .$
Substituting the reference point $(2; 5)$ into the equation results in:

$5 = - 5 \cdot 2 + b \Leftrightarrow b = 15 .$
Thus, we have:

$g : y = - 5 x + 15 .$
Transforming the equation of a line into normal form results in

$\frac{1}{2} y + x + 2 = 0 \Leftrightarrow y = - 2 x - 4 .$
The reference point $(b; - 5)$ corresponding to the reference vector $(\begin{matrix} b \\ - 5 \end{matrix})$ must lie on the line, i.e. its coordinates must satisfy the equation of the line:

$- 5 = - 2 b - 4 \Leftrightarrow b = \frac{1}{2} .$
The position vectors of the points on $h$ have the form $(\begin{matrix} x \\ - 2 x - 4 \end{matrix}) = x (\begin{matrix} 1 \\ - 2 \end{matrix}) + (\begin{matrix} 0 \\ - 4 \end{matrix})$ , so $(\begin{matrix} 1 \\ - 2 \end{matrix})$ is the direction vector of $h$ . Other direction vectors of $h$ are collinear to this vector. Since

$- 1 \cdot (\begin{matrix} 1 \\ - 2 \end{matrix}) = (\begin{matrix} - 1 \\ 2 \end{matrix})$
we have $a = - 1$ .
From the given points $A$ and $B$ , we have for the direction vector

$\vec{A B} = \vec{B} - \vec{A} = (\begin{matrix} 3 \\ - \frac{3}{2} \end{matrix}) - (\begin{matrix} - 2 \\ - 1 \end{matrix}) = (\begin{matrix} 5 \\ - \frac{1}{2} \end{matrix}) .$
The direction vectors in the cases (ii) and (v) are not collinear to this vector. Thus, (ii) and (v) do not represent the line $A B$ correctly. From the direction vector $\vec{A B} = (\begin{matrix} 5 \\ - \frac{1}{2} \end{matrix})$ , we know the slope $m = \frac{- \frac{1}{2}}{5} = - \frac{1}{10}$ of the line $A B$ . Thus, the equation of the line is

$A B : y = - \frac{1}{10} x + b,$
and substituting the coordinates of $A$ into the equation results in the following value of the $y$ -intercept $b$ :

$- 1 = - \frac{1}{10} \cdot (- 2) + b \Leftrightarrow b = - \frac{6}{5} .$
Hence, we have

$A B : y = - \frac{1}{10} x - \frac{6}{5} .$
The equation of the line is satisfied by the coordinates of the reference points in cases (i) to (v) but not by the coordinates of the reference point in the case (vi). Thus, the parametric equations in the cases (i), (iii), and (iv) represent the line correctly, the equations in the cases (ii), (v), and (vi), however, do not.
The condition

$(\begin{matrix} - 2 \\ ψ \end{matrix}) = τ (\begin{matrix} 1 \\ - 3 \end{matrix}) + (\begin{matrix} - 1 \\ 2 \end{matrix})$
results in the two equations

$- 2 = τ - 1 und ψ = - 3 τ + 2 .$
Thus, we first have $τ = - 1$ and hence, $ψ = - 3 \cdot (- 1) + 2 = 5$ .

In contrast to lines in the plane, lines in space cannot be described by an equation of a line in coordinate form. However, the description by a parametric equation can be easily extended from two to three dimensions (see Info Box below).

Info 10.2.5

A line

g

in space is given in vector form or parametric form as the set of position vectors

g = {\vec{r} = λ \vec{u} + \vec{a} \in ℝ^{3} : λ \in ℝ},

often written in short as

g : \vec{r} = λ \vec{u} + \vec{a}, λ \in ℝ .

As in the two-dimensional case:

λ

is called a parameter,

\vec{a}

is called the reference vector, and

\vec{u} \neq \vec{O}

is called the direction vector of the line

g

(see figure below).

In this three-dimensional case, as in the plane, the parametric form of the equation of a line is not unique. The example below lists a few applications of parametric equations of a line in space.

Example 10.2.6

Let the two points

P = (- 1; - 2; \frac{1}{2})

and

Q = (2; 0; 8)

in space be given. Find two different representations of the line

P Q

in parametric form.
We use the connecting vector

\vec{P Q}

as direction vector:

\vec{P Q} = \vec{Q} - \vec{P} = (\begin{matrix} 2 \\ 0 \\ 8 \end{matrix}) - (\begin{matrix} - 1 \\ - 2 \\ \frac{1}{2} \end{matrix}) = (\begin{matrix} 3 \\ 2 \\ \frac{15}{2} \end{matrix}) .

The point

Q

can be used as reference point. For the parametric form we get

P Q : \vec{r} = t (\begin{matrix} 3 \\ 2 \\ \frac{15}{2} \end{matrix}) + (\begin{matrix} 2 \\ 0 \\ 8 \end{matrix}), t \in ℝ .

Further possible direction vectors must be collinear to the vector

\vec{P Q}

. For example:

(\begin{matrix} - 6 \\ - 4 \\ - 15 \end{matrix}) = - 2 (\begin{matrix} 3 \\ 2 \\ \frac{15}{2} \end{matrix}) .

We can also use the point

P

as reference point which results in

P Q : \vec{r} = s (\begin{matrix} - 6 \\ - 4 \\ - 15 \end{matrix}) + (\begin{matrix} - 1 \\ - 2 \\ \frac{1}{2} \end{matrix}), s \in ℝ

as another correct equation of the line

P Q

in vector form.

Exercise 10.2.7

The line $h = A B$ through the points $A = (- 1; - 1; 0)$ and $B = (- 3; 0; 1)$ has the parametric equation

$h : \vec{r} = λ (\begin{matrix} 4 \\ a \\ b \end{matrix}) + (\begin{matrix} c \\ d \\ - 4 \end{matrix}), λ \in ℝ .$
Find the missing values of $a$ , $b$ , $c$ , and $d$ .
$a =$

$b =$

$c =$

$d =$
Find the value of $χ$ such that the point $P$ with the position vector

$\vec{P} = (\begin{matrix} - 2 \\ χ \\ - 8 \end{matrix})$
lies on the line

$g : \vec{r} = ν (\begin{matrix} 1 \\ - 3 \\ 8 \end{matrix}) + (\begin{matrix} - 1 \\ 2 \\ 0 \end{matrix}), ν \in ℝ,$
and find the value of the parameter $ν$ such that $\vec{r} = \vec{P}$ .
$χ =$

$ν =$

From the given points $A$ and $B$ , we have for the direction vector

$\vec{A B} = \vec{B} - \vec{A} = (\begin{matrix} - 3 \\ 0 \\ 1 \end{matrix}) - (\begin{matrix} - 1 \\ - 1 \\ 0 \end{matrix}) = (\begin{matrix} - 2 \\ 1 \\ 1 \end{matrix}) .$
Thus, $(\begin{matrix} 4 \\ a \\ b \end{matrix})$ is collinear to $(\begin{matrix} - 2 \\ 1 \\ 1 \end{matrix})$ , and hence it is also a possible direction vector of $h$ for $a = b = - 2$ since in this case, we have

$(\begin{matrix} 4 \\ - 2 \\ - 2 \end{matrix}) = - 2 \cdot (\begin{matrix} - 2 \\ 1 \\ 1 \end{matrix}) .$
The reference vector $(\begin{matrix} c \\ d \\ - 4 \end{matrix})$ must correspond to a point on $h$ . Using $\vec{A B}$ as direction vector and $\vec{A}$ as reference vector, one possible equation of the line $h$ in parametric form is

$h : \vec{r} = t (\begin{matrix} - 2 \\ 1 \\ 1 \end{matrix}) + (\begin{matrix} - 1 \\ - 1 \\ 0 \end{matrix}), t \in ℝ .$
This results in the equation

$(\begin{matrix} c \\ d \\ - 4 \end{matrix}) = t (\begin{matrix} - 2 \\ 1 \\ 1 \end{matrix}) + (\begin{matrix} - 1 \\ - 1 \\ 0 \end{matrix}) = (\begin{matrix} - 2 t - 1 \\ t - 1 \\ t \end{matrix}),$
and from the third component we immediately read off $t = - 4$ . Thus, we have

$(\begin{matrix} c \\ d \\ - 4 \end{matrix}) = - 4 \cdot (\begin{matrix} - 2 \\ 1 \\ 1 \end{matrix}) + (\begin{matrix} - 1 \\ - 1 \\ 0 \end{matrix}) = (\begin{matrix} 7 \\ - 5 \\ - 4 \end{matrix})$
and hence $c = 7$ and $d = - 5$ .
The condition

$(\begin{matrix} - 2 \\ χ \\ - 8 \end{matrix}) = ν (\begin{matrix} 1 \\ - 3 \\ 8 \end{matrix}) + (\begin{matrix} - 1 \\ 2 \\ 0 \end{matrix}) = (\begin{matrix} ν - 1 \\ - 3 ν + 2 \\ 8 ν \end{matrix})$
results for the first and the third component in $ν = - 1$ , and from the second component we have $χ = - 3 \cdot (- 1) + 2 = 5$ .

Onlinebrückenkurs Mathematik

1. Elementary Arithmetic

2. Equations in one Variable

3. Inequalities in one Variable

4. System of Linear Equations

5. Geometry

6. Elementary Functions

7. Differential Calculus

8. Integral Calculus

9. Objects in the Two-Dimensional Coordinate System

10. Basic Concepts of Descriptive Vector Geometry

11. Language of Descriptive Statistics