Chapter 4 System of Linear Equations
Section 4.3 LS in three Variables4.3.2 Solvability and Comparison Method, graphical Interpretation
As described in section 4.2 for systems of two linear equations in two variables, the question for solvability and the solution of the system can be traced back very clearly to the question for existence and position of the intersection point of two lines. And of course, one should think about whether for systems of three linear equations a similar graphical interpretation can be found.If the previous two-dimensional space (for the variables and ) is supplemented by another dimension or variable, namely , then using a linear equation in this three variables
a plane is represented in general form. This equation is similar to the equation of a line we already investigated. For , this equation can be solved for :
which is the explicit form of the equation of the very same plane. The last equation assigns every pair , i.e. every point in the --plane, a value , i.e. a height in three-dimensional space. Thus, a surface above the --plane is created, which is a plane due to the linearity of the equation.
Now, not only the first equation of the system 4.3.2 has to be satisfied but simultaneously also the second and third equation which can be graphically interpreted as planes as well. If we are now interested in the solution of a system of three linear equations, we have to investigate - in the graphical interpretation - the intersection behaviour of three planes. On this point, let us first investigate an example.
Example 4.3.3
Find the solution set of the following system of linear equations
The base set is the set of real numbers .
Each of the three equations can be solved for easily:
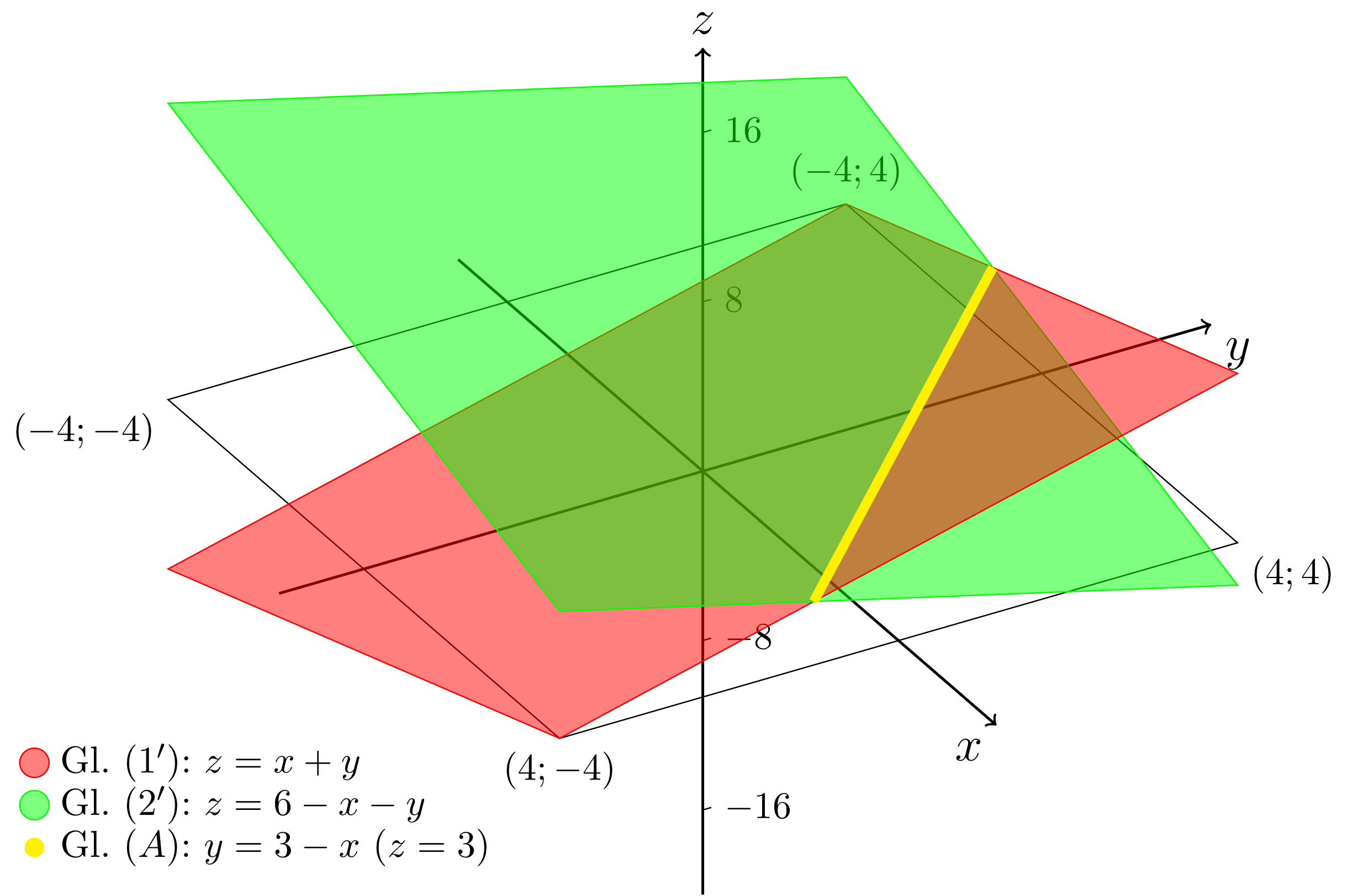
Equating the right-hand sides of equation and equation corresponds graphically to the determination of the intersection line of the two planes described by these equations:
Substituting this relation into equation or equation results in an equation for the -coordinate of the intersection line; in this case we have . The following figure shows this intersection line described by equation as the intersection of the two non-parallel planes described by equation and equation .
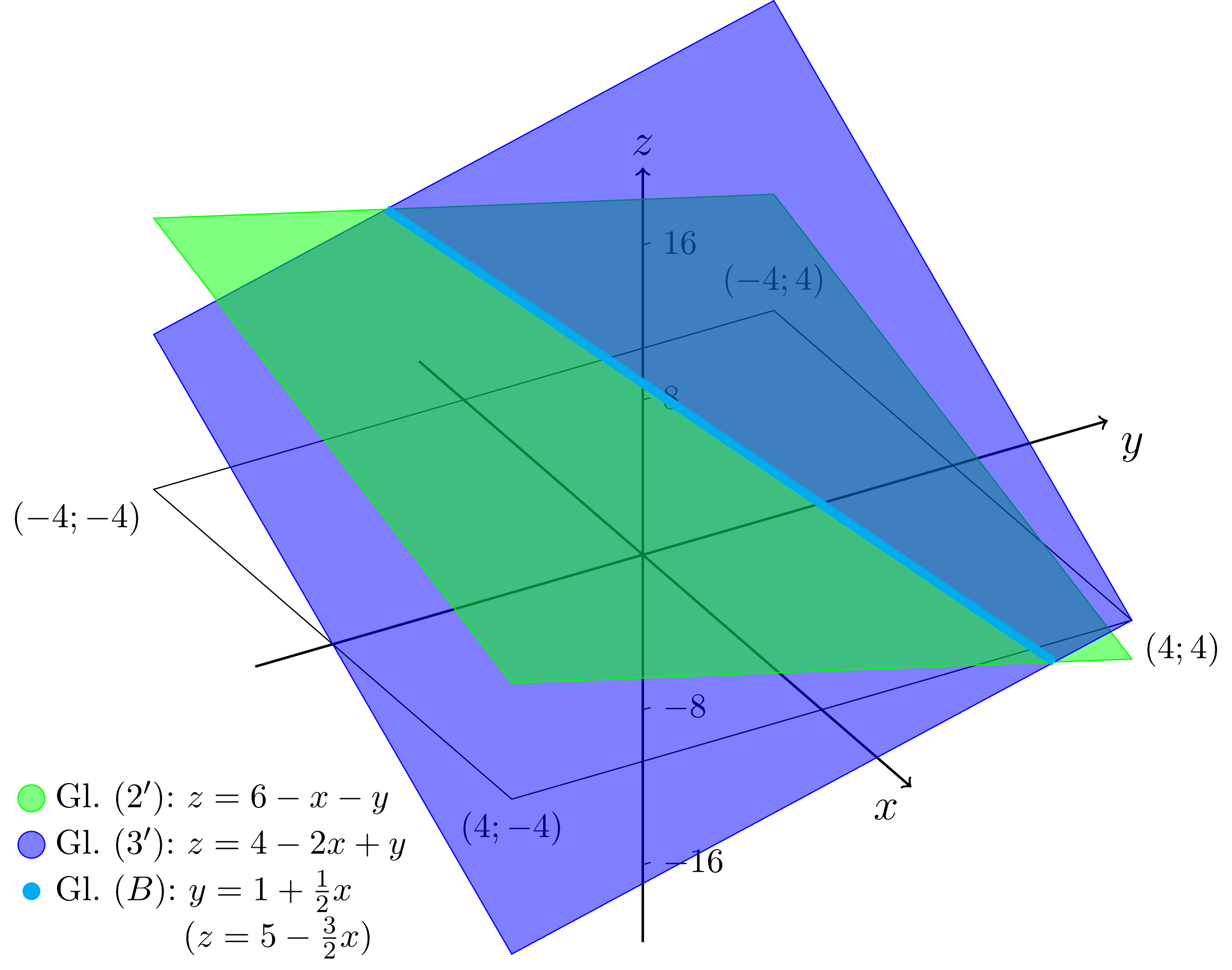
The totally analogous statement holds if the right-hand sides of equation and equation are equated. Then, one obtains for the intersection line of the planes and :
Substituting this relation into equation or equation results in an equation for the -coordinate of the intersection line; in this case we have . The following figure shows the intersection line described by equation as the intersection of the two non-parallel planes described by equation and equation .
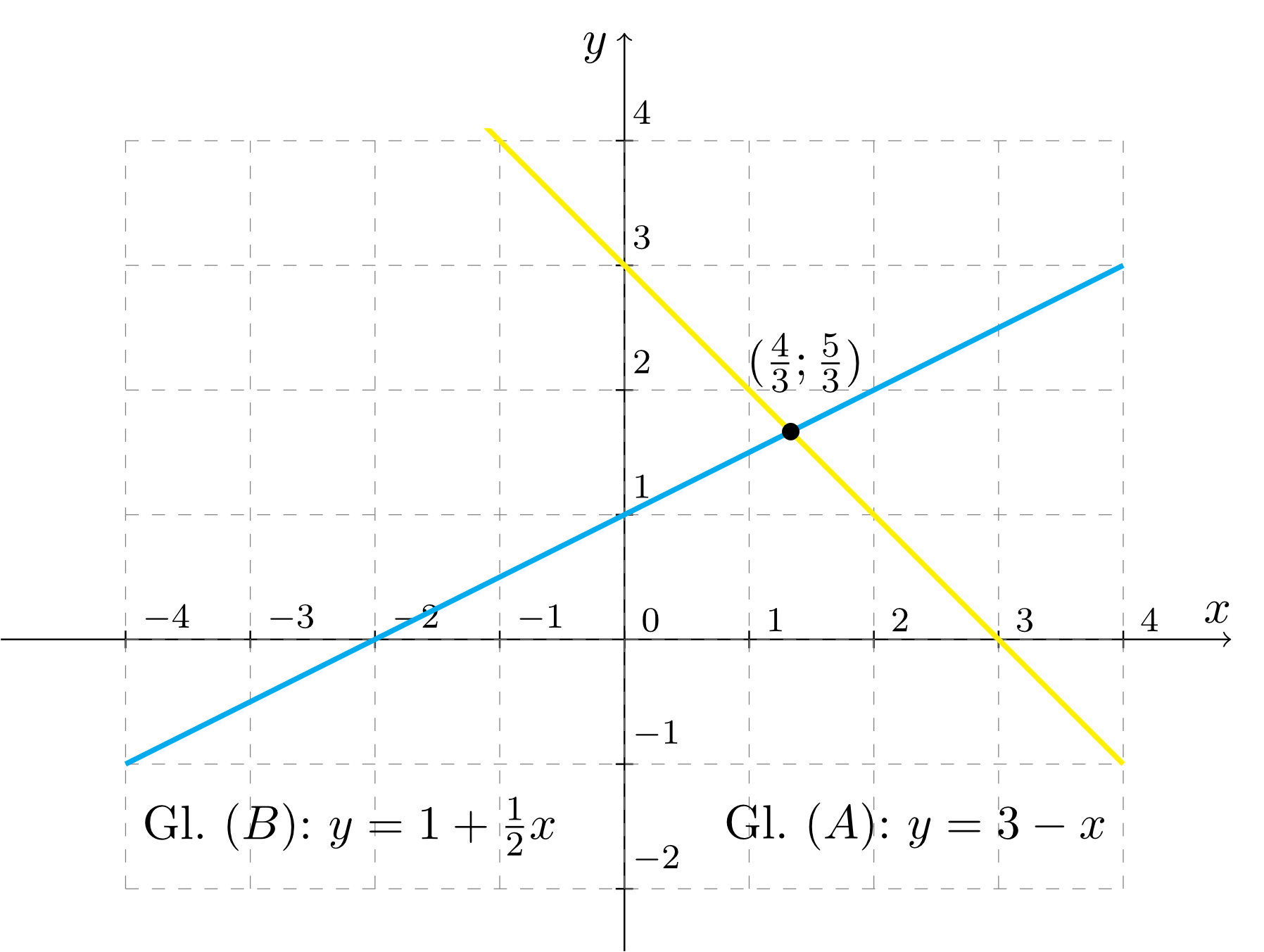
Since all equations in the initial linear system have to hold simultaneously, the two equations for the two intersection lines of the three planes also have to hold simultaneously. Graphically, this is the case at the intersection point of the intersection lines. This intersection point is found by equating the right-hand sides of equation and equation :
The value of can be calculated by inserting the value of , for example, in equation :
The following figure shows the intersection lines described by equation and equation in the --plane (view from above) and their intersection point.
Finally, the value of results by inserting the values of and , for example, in equation :
Thus, the given system of linear equations has a unique solution. The solution set is .
The base set is the set of real numbers .
Each of the three equations can be solved for easily:
Equating the right-hand sides of equation and equation corresponds graphically to the determination of the intersection line of the two planes described by these equations:
Substituting this relation into equation or equation results in an equation for the -coordinate of the intersection line; in this case we have . The following figure shows this intersection line described by equation as the intersection of the two non-parallel planes described by equation and equation .
The totally analogous statement holds if the right-hand sides of equation and equation are equated. Then, one obtains for the intersection line of the planes and :
Substituting this relation into equation or equation results in an equation for the -coordinate of the intersection line; in this case we have . The following figure shows the intersection line described by equation as the intersection of the two non-parallel planes described by equation and equation .
Since all equations in the initial linear system have to hold simultaneously, the two equations for the two intersection lines of the three planes also have to hold simultaneously. Graphically, this is the case at the intersection point of the intersection lines. This intersection point is found by equating the right-hand sides of equation and equation :
The value of can be calculated by inserting the value of , for example, in equation :
The following figure shows the intersection lines described by equation and equation in the --plane (view from above) and their intersection point.
Finally, the value of results by inserting the values of and , for example, in equation :
Thus, the given system of linear equations has a unique solution. The solution set is .
- If (at least) two of the three planes are parallel to each other (without being congruent), the system has no solution: Planes that are parallel (without being congruent) do not intersect and hence the equations describing the planes cannot hold simultaneously.
- If two of the three planes are congruent, the intersection set with the third (non-parallel) plane is an intersection line. All points on this intersection line are solutions of the system. Hence, the solution set is infinite.
- If the three planes are congruent, all points of the (congruent) planes are solutions of the system. Again, the solution set is infinite.
- A unique solution can only exist in this last case: The three (non-parallel and non-congruent) planes have three intersection lines (intersection of plane and plane , intersection of plane and plane , and intersection of plane and plane ):
- If two of the three intersection lines are parallel, the system has no solution.
- If two of the three intersection lines are congruent, the system has an infinite number of solutions.
- If the three intersection lines intersect in one point, the solution is unique and the solution set consists of exactly one element.
- If two of the three intersection lines are parallel, the system has no solution.
By the way, in the above example 4.3.3 it is not necessary to find the third intersection line and to check whether this third intersection line intersects the two other lines in their intersection point: This is automatically true since equating the right-hand sides of equation and equation (first intersection line/equation ) and equating the right-hand sides of equation and equation (second intersection line/equation ) guaranties the validity of the equation of the third intersection line (right-hand side of = right-hand side of ):
In the example, the comparison method was used since it relates very closely to the geometric interpretation. Equating explicit equations of planes or lines, respectively, corresponds precisely to the determination of intersection lines and points.
Info 4.3.4
In the comparison method, as a first step the three linear equations are solved for one of the variables - or for a multiple of one of the variables. Then, the resulting new equations are equated in pairs. It is sufficient to equate two pairs. Altogether, a system of two linear equations in only two variables results, which can be subsequently be investigated using methods described in section 4.2.
Exercise 4.3.5
Find the solution set of the following system of linear equations
Use the comparison method and be clever!
Use the comparison method and be clever!
 Onlinebrückenkurs Mathematik
Onlinebrückenkurs Mathematik