Chapter 4 System of Linear Equations

Section 4.4 More general Systems

4.4.3 Exercises

Exercise 4.4.3

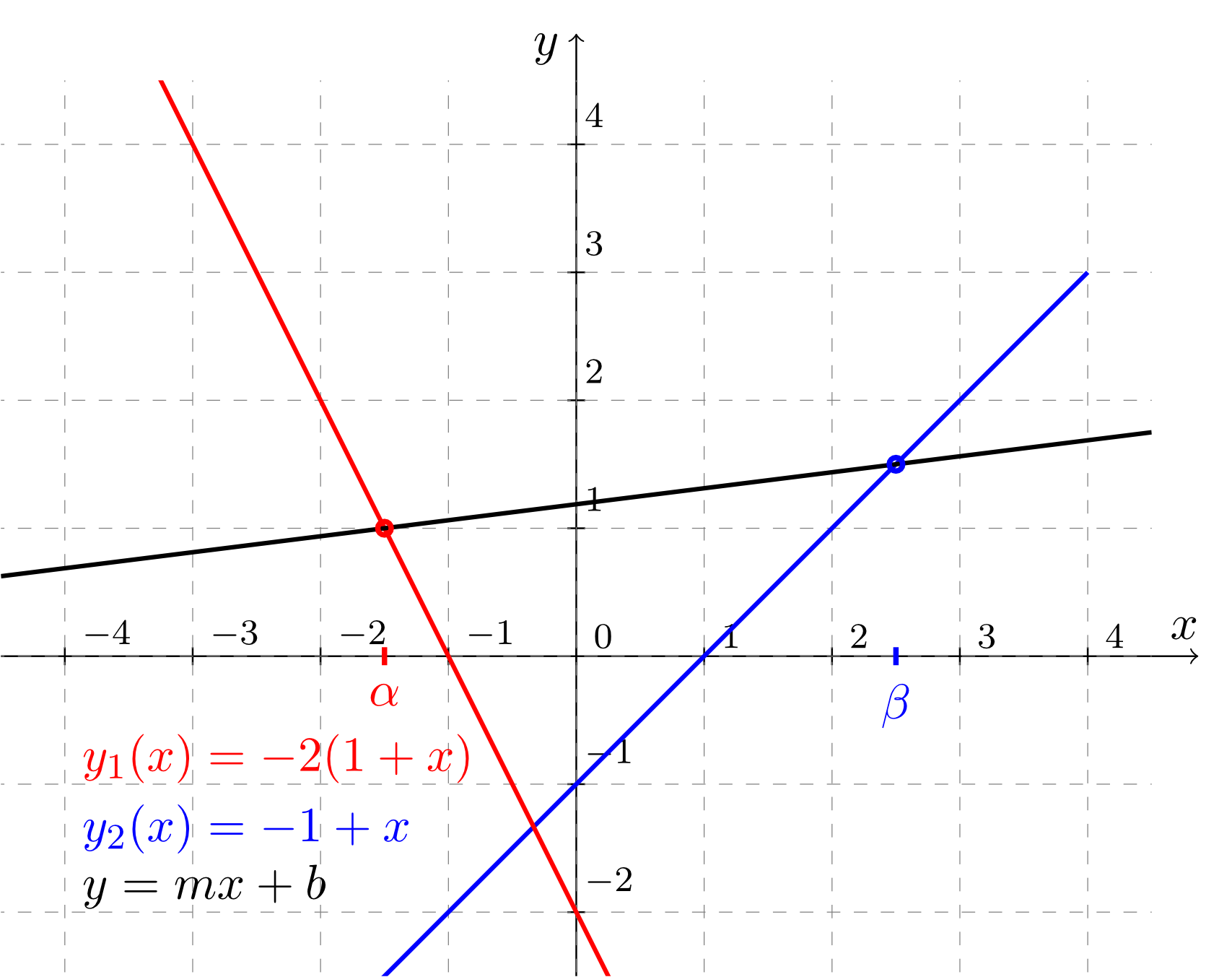
Find the

y

-intercept

b

and the slope

m

of a line described by the equation

y = m x + b

which is defined by two points. The first point at

x_{1} = α

lies on the line described by the equation

y_{1} (x) = - 2 (1 + x)

. The second point at

x_{2} = β

lies on the line described by the equation

y_{2} (x) = x - 1

. The following figure illustrates the situation.

Find the system of equations for the parameters $b$ and $m$ .
The first equation reads $m α + b$ $=$
;
the second equation reads $m β + b$ $=$
.
The constants $α$ and $β$ have to remain in the solution; for these alpha and beta can be entered.
Solve this system of equations for $b$ and $m$ . For which values of $α$ and $β$ does the system have a unique solution, no solution, or an infinite number of solutions?
For $α = - 2$ and $β = 2$ one obtains, for example, the solution $m$ $=$
and $b$ $=$
, the case $α = 2$ and $β = - 2$ results in the solution $m$ $=$
and $b$ $=$ .
The LS has an infinite number of solutions if $α$ $=$
and $β$ $=$ .
The corresponding solutions can be parameterised by $m = r$ and $b$ $=$
, $r \in ℝ$ .
What is the graphical interpretation of the last two cases, i.e. no solution and an infinite number of solutions?

>From the condition

$y (x_{1} = α) = y_{1} (x_{1} = α) and y (x_{2} = β) = y_{2} (x_{2} = β)$
the LS for $m$ and $b$ results in:

$\begin{matrix} m α + b & = & - 2 (1 + α) & equation (1), \\ m β + b & = & - 1 + β & equation (2) . \end{matrix}$
If equation $(2)$ is replaced by the difference of equation $(2)$ and equation $(1)$ , one obtains

$\begin{matrix} m α + b & = & - 2 (1 + α) & equation (1), \\ m (β - α) & = & 1 + 2 α + β & equation (2') . \end{matrix}$
With this, the LS has already triangular form.

A. For $β - α \neq 0 \Leftrightarrow β \neq α$ equation $(2')$ can be divided by $(β - α)$ , which for the slope $m$ results in

$m = \frac{1 + 2 α + β}{β - α} .$
For example, this result can be substituted into equation $(1)$ resolved for $b$ :

$b = - 2 (1 + α) - m α = - 2 (1 + α) - \frac{1 + 2 α + β}{β - α} α .$
The obtained values of $m$ and $b$ represent a unique solution of the considered LS.
For $α = - 2$ , $β = 2$ , the solution is $m = - 1 / 4, b = 5 / 2$ , and for $α = 2$ , $β = - 2$ the solution is $m = - 3 / 4, b = - 9 / 2$ .

B. In this case $β - α = 0 \Leftrightarrow β = α$ . So, the left-hand side of equation $(2')$ is zero. Thus, the following additional case analysis is required:
Ba. If the right-hand side of equation is non-zero, i.e. $(2')$ $1 + 2 α + β \neq 0$ , the LS has no solution, i.e. $L = ∅$ . For $β = α$ one obtains $β = α \neq - \frac{1}{3}$ .
Bb. If the right-hand side of equation $(2')$ is zero, the LS only consists of equation $(1)$ with $β = α = - \frac{1}{3}$ . In this case $m = λ$ , $λ \in ℝ$ can be chosen arbitrary, and $b$ results directly from equation $(1)$ : $b = \frac{1}{3} λ - \frac{4}{3}$ . Thus, the solution set of the LS is

$L = {(m = λ; b = \frac{1}{3} λ - \frac{4}{3}) : λ \in ℝ} .$
The right-hand sides of equation $(1)$ and equation $(2)$ contain the $y$ -values of the initial lines at $x_{1} = α$ and $x_{2} = β$ , i.e. $y_{1} (α)$ and $y_{2} (β)$ , such that the right-hand side of equation $(2')$ is the difference $y_{2} (β) - y_{1} (α)$ . In case B, i.e. for $β = α$ , one then obtains $y_{2} (α) - y_{1} (α)$ . So, the LS has no solution (case Ba) if $y_{2} (α) - y_{1} (α) \neq 0$ $\Leftrightarrow$ $y_{2} (α) \neq y_{1} (α)$ , i.e. the two lines have different $y$ -values. On the other hand an infinite number of solutions exist (case Bb) if the two initial equations intersect at $x = α$ .

Exercise 4.4.4

Find the solution set of the following LS depending on the parameter

t \in ℝ

\begin{matrix} x - y + t z & = & t & equation (1), \\ t x + (1 - t) y + (1 + t^{2}) z & = & - 1 + t & equation (2), \\ (1 - t) x + (- 2 + t) y + (- 1 + t - t^{2}) z & = & t^{2} & equation (3) . \end{matrix}

The LS only has solutions for the following values of the parameter:

t \in

.
Set can be entered in the form ${$ a;b;c; $\dots}$ . The empty set can be entered as

{}

.
For the smallest value of the parameter

t

the solution is

x

=

y

=

z = r

r \in ℝ

.
For the greatest value of the parameter

t

the solution is

x

=

y

=

z = r

r \in ℝ

As a first step, equation

(3)

is replaced by the sum of equation

(2)

and equation

(3)

\begin{matrix} x - y + t z & = & t & equation (1), \\ t x + (1 - t) y + (1 + t^{2}) z & = & - 1 + t & equation (2), \\ x - y + t z & = & - 1 + t + t^{2} & equation (3') . \end{matrix}

Since the left-hand side of equation

(1)

and equation

(3')

coincide, it is useful to replace equation

(3')

by the sum of the negative of equation

(1)

and equation

(3')

\begin{matrix} x - y + t z & = & t & equation (1), \\ t x + (1 - t) y + (1 + t^{2}) z & = & - 1 + t & equation (2), \\ 0 & = & - 1 + t^{2} & equation (3'') . \end{matrix}

subsequently, replacing equation

(2)

by the sum of

(- t)

-times equation

(1)

and equation

(2)

results in a LS in triangular form:

\begin{matrix} x - y + t z & = & t & equation (1), \\ y + z & = & - 1 + t - t^{2} & equation (2'), \\ 0 & = & - 1 + t^{2} & equation (3'') . \end{matrix}

Finally, adding equation

(2')

to equation

(1)

results in a further simplification,

\begin{matrix} x + (1 + t) z & = & - 1 + 2 t - t^{2} & equation (1'), \\ y + z & = & - 1 + t - t^{2} & equation (2'), \\ 0 & = & - 1 + t^{2} & equation (3'') . \end{matrix}

This equivalent LS only has a solution if equation

(3'')

is satisfied as well, i.e.

0 = - 1 + t^{2}

\Leftrightarrow

t^{2} = 1

. In all other cases the solution set is the empty set, i.e.

L = ∅ für t \in ℝ ∖ {- 1; 1} .

If equation

(3'')

is now satisfied, i.e.

t = 1

t = - 1

, then

z

can be chosen arbitrarily, i.e.

z = λ

λ \in ℝ

. Solving equation

(1')

and equation

(2')

for

x

and

y

, respectively, for

t = 1

results in the expressions

x = - 2 z

and

y = - 1 - z

, so the solution set is

L = {(x = - 2 λ; y = - 1 - λ; z = λ) : λ \in ℝ} for t = 1 .

Accordingly, for

t = - 1

one obtains

x = - 4

and

y = - 3 - z

, so the solution set is

L = {(x = - 4; y = - 3 - λ; z = λ) : λ \in ℝ} for t = - 1 .

Onlinebrückenkurs Mathematik

1. Elementary Arithmetic

2. Equations in one Variable

3. Inequalities in one Variable

4. System of Linear Equations

5. Geometry

6. Elementary Functions

7. Differential Calculus

8. Integral Calculus

9. Objects in the Two-Dimensional Coordinate System

10. Basic Concepts of Descriptive Vector Geometry

11. Language of Descriptive Statistics

Chapter 4 System of Linear Equations

4.4.3 Exercises

Exercise 4.4.3

Exercise 4.4.4