4.5.1 Final Test Module 4

This is a test for submission:

Unlike open exercises, no hints for formulating mathematical expressions are provided.
The test can be restarted or interrupted at any time.
The test can be terminated and submitted using the buttons at the end of the page, or reset.
The test can be attempted several times. Only the last version will be included in the statistics.

Find the solution set of the following system of linear equations:

\begin{matrix} - x + 2 y & = & - 5, \\ 3 x + y & = & 1 . \end{matrix}

The solution set

	is empty,
	contains exactly one element: $x =$ , $y =$ ,
	contains an infinite number of solution pairs $(x; y)$ .

Find the two-digit number such that its digit sum is 6 and exchanging the tens and the units digit results in a number which is 18 less. Answer:
.

Find the value of the real parameter

α

for which the following system of linear equations

\begin{matrix} 2 x + y & = & 3, \\ 4 x + 2 y & = & α \end{matrix}

has an infinite number of solutions.
Answer:

α =

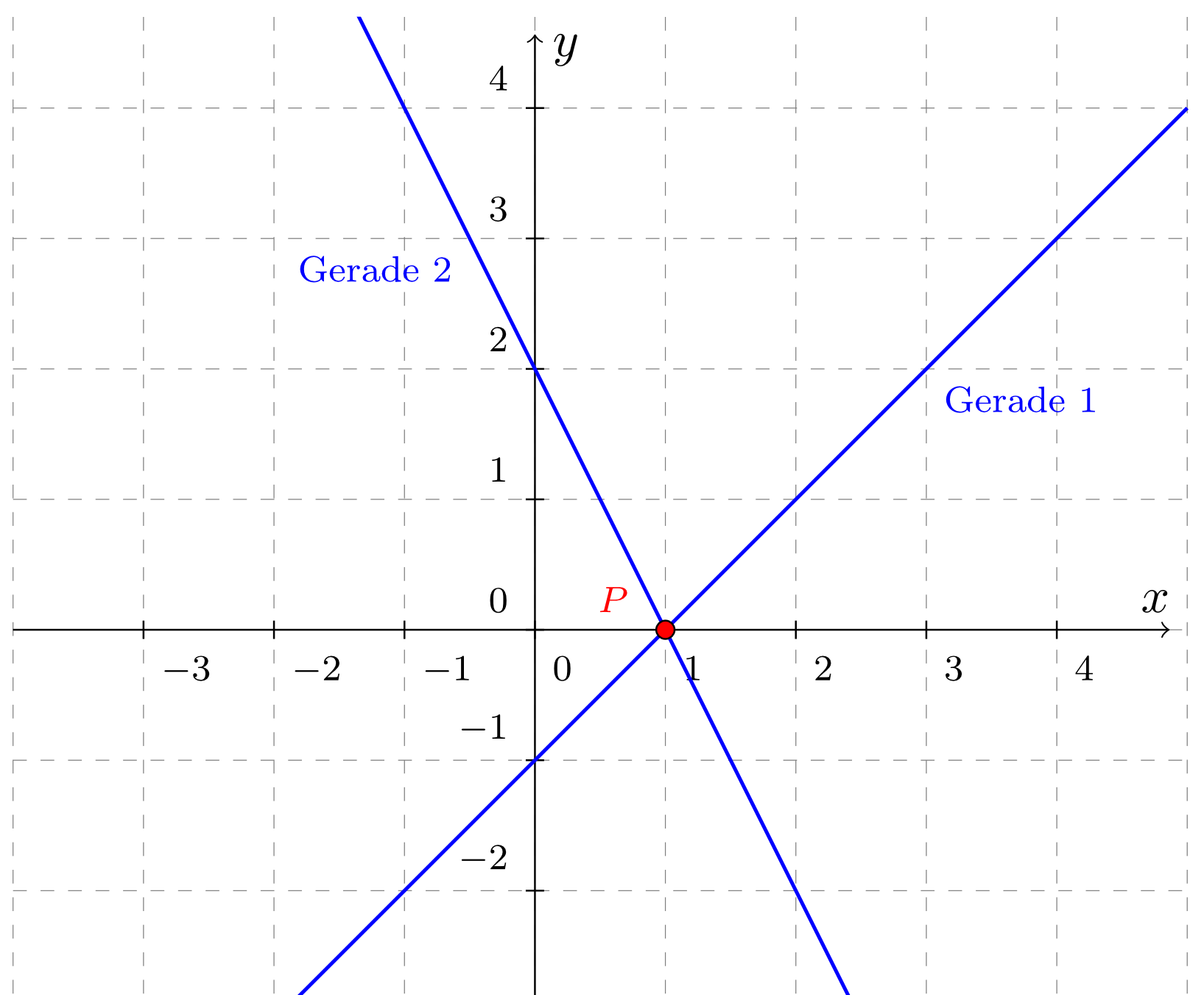
The following figure shows two lines in two-dimensional space.

Find the two equations describing the lines.
Line 1:

y =

,
Line 2:

y =

.
What is the number of solutions of the corresponding system of linear equations?
The system of linear equations has

	no solution,
	exactly one solution, or
	an infinite number of solutions.

Find the solution set of the following system of linear equations consisting of three equations in three variables:

\begin{matrix} x + 2 z & = & 3, \\ - x + y + z & = & 1, \\ 2 y + 3 z & = & 5 . \end{matrix}

The solution set

	is empty,
	contains exactly one solution: $x =$ , $y =$ , $z =$ ,
	contains an infinite number of solutions $(x; y; z)$ .

The test evaluation will be displayed here!