Chapter 4 System of Linear Equations
Section 4.3 LS in three Variables4.3.5 Exercises
Exercise 4.3.10
Find the solution set of the following system of linear equations
using
using
- the substitution method,
- the addition method.
Exercise 4.3.11
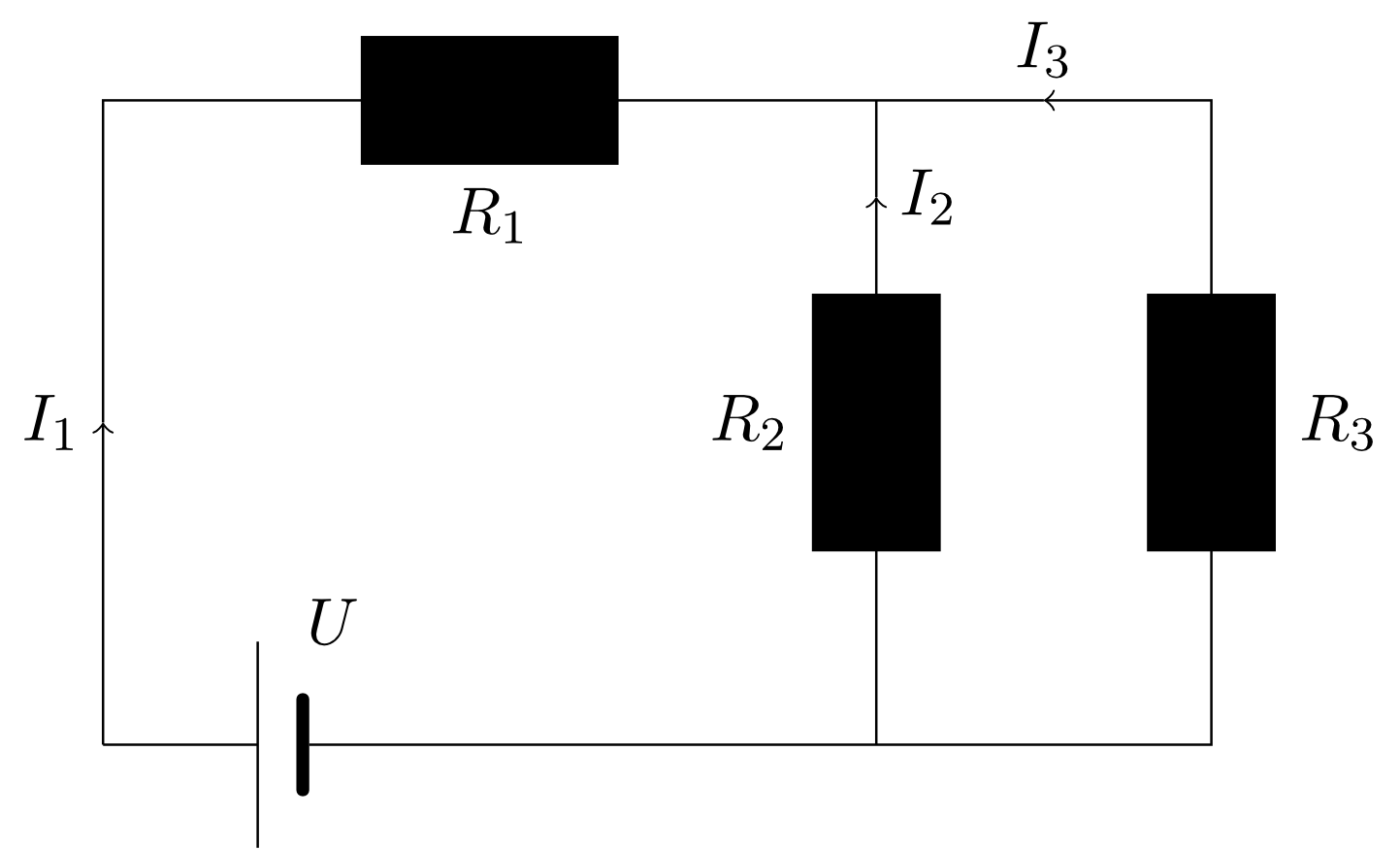
Consider the following circuit: It consists of a source providing a voltage of and three resistors , , and . Find the currents , , and in the loops.
Hints: The relations between voltages, resistances, and currents in such circuits are described by the so-called Kirchhoff's rules which in this example result in the following three equations:
Additionally, the relation between the physical units Volt () (voltage), Ampère () (current) und Ohm () (resistance) is used: .
Hints: The relations between voltages, resistances, and currents in such circuits are described by the so-called Kirchhoff's rules which in this example result in the following three equations:
Additionally, the relation between the physical units Volt () (voltage), Ampère () (current) und Ohm () (resistance) is used: .
Exercise 4.3.12
Find the solution set of the following system of equations using the addition method:
 Onlinebrückenkurs Mathematik
Onlinebrückenkurs Mathematik