Chapter 8 Integral Calculus

Section 8.2 Definite Integral

8.2.2 Integral


The integral of a function f with f(x)≥0 can be interpreted as the "area under the graph" of the function. In the so-called Riemann integral, the graph of the function is approximated by a step function, and the values of this step function are summed up, weighted by the corresponding interval length, i.e. the "width of a step". This approach is illustrated in the figure below.

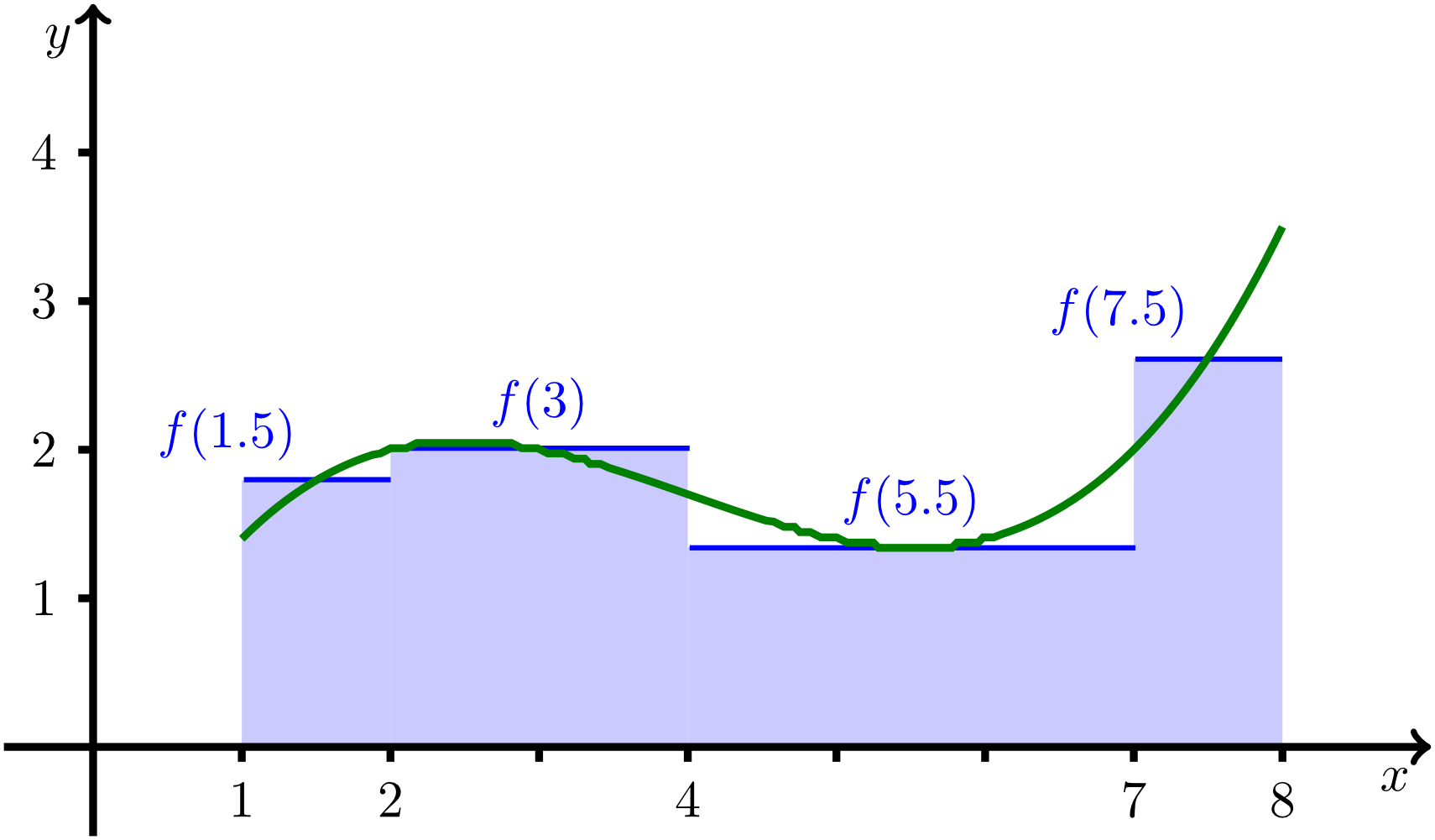
Definition of the Riemann integral. The function is approximated by a step function that is divided here into four subintervals.
We can see here that the area under the graph of the function is initially approximated by rectangles. The length of the (horizontal) side of these rectangles is determined by the length of an interval on the x-axis, while the length of the second (vertical) side is determined by a function value f( zk ) at the point zk in the corresponding x-interval. Then the areas of these rectangles are calculated, and finally summed up. The smaller the intervals on the x-axis, the more the sum calculated this way approaches the "real" value of the area under the graph (the correct integral value of the function).
Formally, a sum Sn of the form

Sn = ∑k=0 n-1f( zk )·Δ( xk )       with   Δ( xk )= xk+1 - xk

is calculated. In the example considered here, the interval [0;8] is divided into four parts, where x0 =1, x1 =2, x2 =4, and x3 =7. If the areas of these four parts are summed according to the formula above, this results in

S4 = f( z0 )·( x1 - x0 )+f( z1 )·( x2 - x1 )+f( z2 )·( x3 - x2 )+f( z3 )·( x4 - x3 ) = f( z0 )·(2-1)+f( z1 )·(4-2)+f( z2 )·(7-4)+f( z3 )·(8-7) = f( z0 )·1+f( z1 )·2+f( z2 )·3+f( z3 )·1 .

To get precise values for the area, it is obviously not sufficient to subdivide the interval into just a few subintervals. In general, it will be necessary to decrease the maximal length of the subintervals xk+1 - xk gradually, which in turn requires more summands f( zk )·( xk+1 - xk ) to be calculated and added. Hence, the limit is considered as the maximal length of the subintervals tends to zero.
In principle, the approach discussed above can also be applied to functions with negative function values. We will explain in Section 8.3 how the area is calculated then. However, note that in the definition of the integral a few aspects have to be observed that go beyond the scope of this course. Therefore, we refer to advanced textbooks for details concerning the assumptions in the definitions below.
Integral 8.2.1
Let a function f:[a;b]→ℝ on a real interval [a;b] be given. If the number of subintervals is increased such that xk+1 - xk approaches 0, then

∫a b f(x) dx= limn→∞ Sn = limn→∞ ∑k=0 n-1f( zk )·( xk+1 - xk )    with    xk ≤ zk ≤ xk+1 (8.2.1)

is called the definite integral of f with the lower limit of integration a and the upper limit of integration b (if the limit exists and does not depend on the respective partition). The function f is then referred to as integrable. In this context the function f is also called the integrand.

In principle, this approach can also result in an indefinite value, i.e. the integral does not exist. However, advanced considerations show that the integral exists for every continuous function. As an example, we calculate the integral of f:[0;1]→ℝ, x↦x, where we focus on the calculation of the limit.
Example 8.2.2
Calculate the integral of f:[0;1]→ℝ, x↦x.
For this purpose, the interval [0;1] is subdivided into subintervals [ xk ; xk+1 ] of equal length with x0 :=0 and xk := xk-1 + 1 n . Thus, the length of a subinterval is Δ( xk )= xk+1 - xk = 1 n .
Investigating the length of the interval for n tending to infinity shows that Δ( xk ) is getting smaller and approaches zero. Thus, the assumption for the calculation of a definite integral is satisfied.
Furthermore, for the values of xk , we obtain from the length of an interval xk = k n . If we set zk = xk for the intermediate points, we obtain f( zk )=f( xk )= xk = k n .
Substituting these terms into the formula (1) gives the equation

Sn = ∑k=0 n-1f( xk )·Δ( xk )= ∑k=0 n-1 xk · 1 n = ∑k=0 n-1 k n · 1 n = 1 n2 · ∑k=0 n-1k= 1 n2 · ∑k=1 n-1k = 1 n2 n(n-1) 2 = 1 2 · n-1 n = 1 2 ·(1- 1 n ) ,

where we used the formula ∑k=1 n-1k= 1 2  n(n-1) of Carl Friedrich Gauss. And with limn→∞ 1 n =0, we find for the integral

∫0 1 x dx= limn→∞ Sn = 1 2  .


The large class of integrable functions includes all polynomials, rational functions, trigonometric functions, exponential functions, logarithmic functions and their compositions.
To simplify the calculations, rules for integrating functions are required that are as easy as possible. An important result is provided by the so-called fundamental theorem of calculus. It describes the relation between the antiderivative of a continuous function and its integral.
Fundamental Theorem of Calculus 8.2.3
Let a continuous function f:[a;b]→ℝ on a real interval [a;b] be given. Then the function f has an antiderivative, and for every antiderivative F of f, we have

∫a b f(x) dx  =   [F(x)]a b   =  F(b)-F(a) .


As a simple example, we will calculate the definite integral of the function f with f(x)= x2 between a=1 and b=2. Using the rules for the determination of antiderivatives and the fundamental theorem of calculus this problem can be solved easily.
Example 8.2.4
The function f:[1;2]→ℝ with f(x):= x2 has the antiderivative F with
F(x)= 1 3 x3 +C for a real number C. From the fundamental theorem, we have

∫1 2 x2  dx= [ 1 3 x3  + C]1 2 =( 1 3   23  + C)-( 1 3   13  + C)= 7 3  .

The calculation shows that the constant is cancelled after substituting the lower and upper limits of integration such that, in practice, it can already be "suppressed" in taking the antiderivative for the definite integral, so for the calculation of the definite integral one can choose C=0.

The equation in the fundamental theorem also applies to every intermediate value z∈[a;b] such that all function values F(z) can be calculated from

F(z)-F(a)= ∫a z f(x) dx ,

if the derivative F'=f and a function value, for example the value F(a), are known. One also says that the antiderivative F is reconstructed from the derivative F'=f.
Application examples for the reconstruction of a function F from its derivative F'=f are discussed at the end of Section 8.3.




: