Chapter 8 Integral Calculus
Section 8.3 Applications8.3.4 Exercises
Exercise 8.3.5
Calculate the area of the region that is bounded by the graph of the function and the -axis.
Answer: .
Answer: .
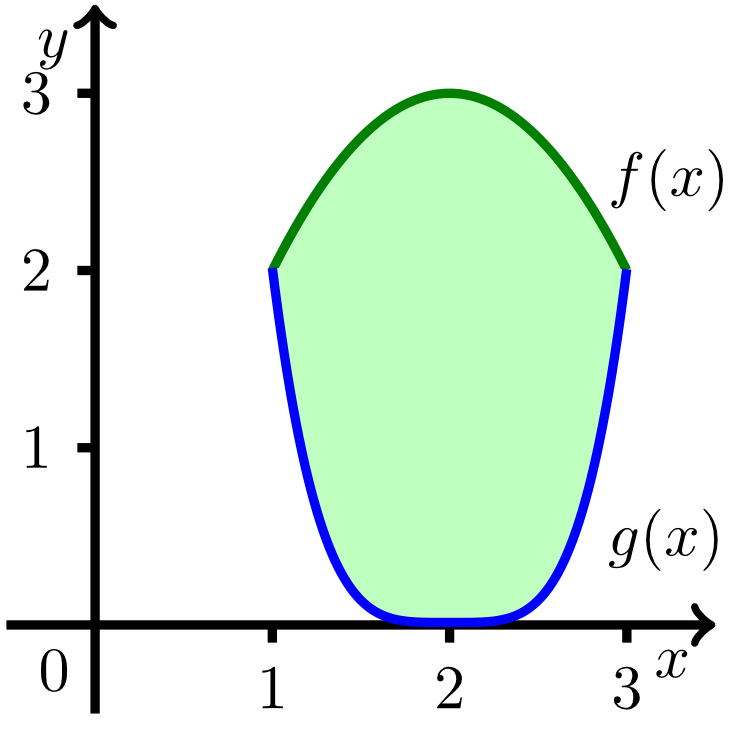
Exercise 8.3.6
Calculate the area of the region bounded by the graphs of the functions and . Draw the graphs of the functions before calculating the area.
Answer: .
Answer: .
In the next exercise, a physical problem will be formulated in mathematical terms, where the description involves a simplification. This shall exemplify that the mathematical notation can, in principle, also be used in applications. In practise, shorter or simpler formulations may occur. For example, domain and range are not given explicitly if they can be deduced from the context.
Exercise 8.3.7
Calculate the work done by a force on a small spherical homogeneous body with mass in lifting it against the gravitational force from the surface of spherical homogeneous body with radius and mass to a height of (all lengths are measured with respect to the centre of the body ). Here, the mass and the gravitational constant are assumed to be given, and the smaller body is assumed to be point-like in comparison to the body .
Answer:
.
The constants and have to occur in the solution, enter as gamma.
Answer:
.
The constants and have to occur in the solution, enter as gamma.
 Onlinebrückenkurs Mathematik
Onlinebrückenkurs Mathematik