Chapter 8 Integral Calculus

Section 8.3 Applications

8.3.2 Calculation of Areas


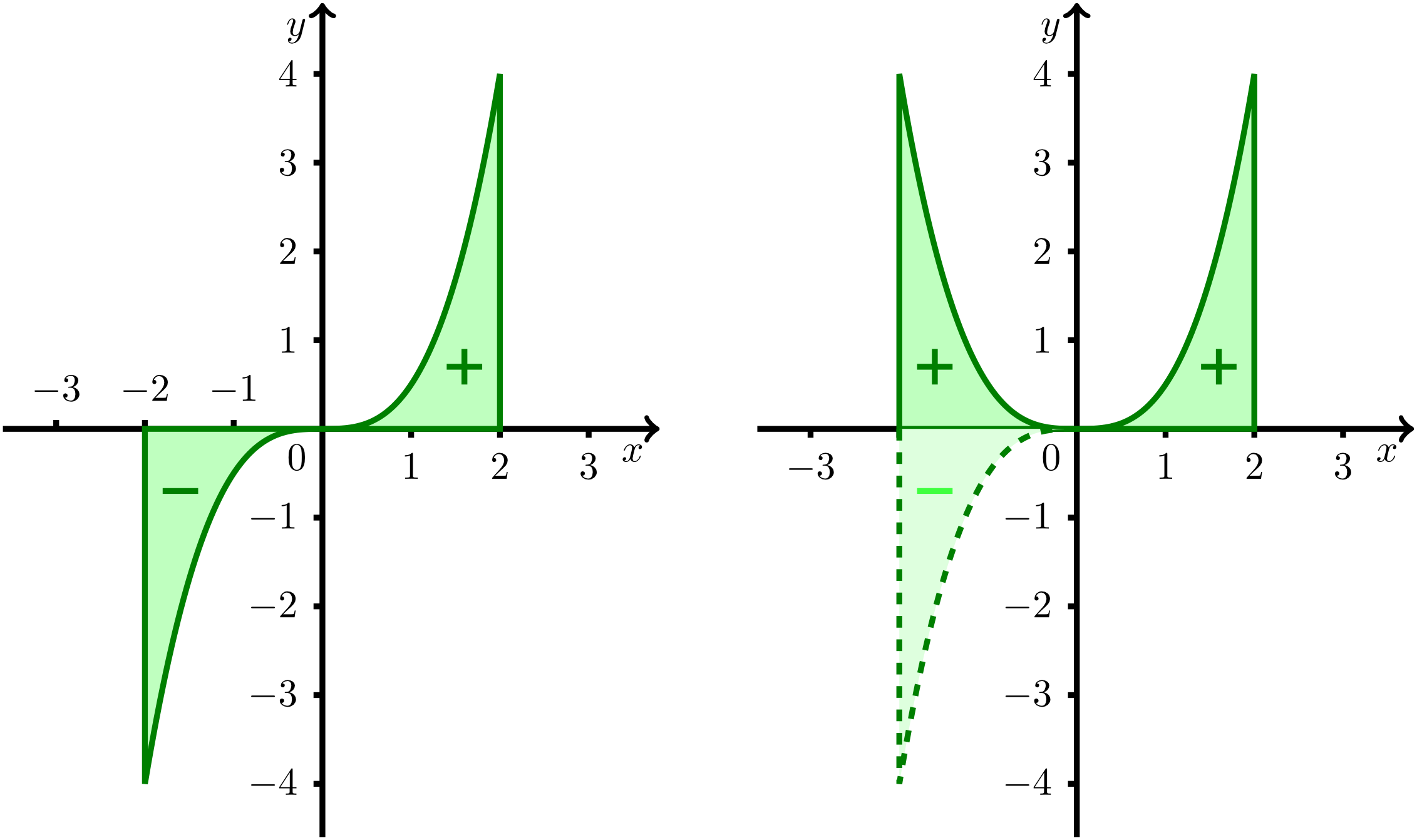
A first application of the integral calculus is the calculation of areas of regions with boundaries that can be described by mathematical functions. For illustration purposes, the figure below (left part) shows the function f(x)= 1 2 x3 on the interval [-2;2]. The goal is to calculate the area that is bounded by the graph of the function and the x-axis. From our previous investigations, we know that the integral over this odd function in the limits from -2 to 2 equals zero since the area of the left region equals the area of the right region but during integration they are assigned different signs. Thus, the value of the integral does not match the actual value of the area. However, if the "negative" area is reflected across the x-axis, i.e. the function is assigned a positive sign (right part of the figure). Now the area is determined correctly by the integral. In mathematical terms, it is not the integral of the function f that is calculated but the integral of its absolute value |f|.

Since the integral is now taken over the absolute value of the function, a partition of the integral depending on the sign of the function is required: the interval of integration is subdivided into subintervals on which the function values have the same sign. For continuous functions, these subintervals are determined by the zeros of the function.
Calculation of Areas 8.3.1
Let a continuous function f:[a;b]→ℝ on an interval [a;b] be given. Moreover, let x1 , ..., xm be the zeros of f with x1 < x2 <…< xm . We set x0 :=a and xm+1 :=b.
Then, the area bounded by the graph of f and the x-axis equals

∫a b |f(x)| dx= ∑k=0 m| ∫ xk xk+1 f(x) dx| .


This shall be explained in more detail for the example above.
Example 8.3.2
We have to calculate the area IA of the region that is bounded by the continuous function f with f(x)= 1 2 x3 and the x-axis on the interval [-2;2]. The only zero of the given function is at x0 =0. The interval of integration is subdivided into the two subintervals [-2;0] and [0;2]. Thus, for the area of the region between the graph of the function and the x-axis we calculate

IA = ∫-2 2 | 1 2 x3 |dx = | ∫-2 0 1 2 x3  dx|+| ∫0 2 1 2 x3  dx| = | [ 1 8 x4 ]-2 0 |+| [ 1 8 x4 ]0 2 | = |0-2|+|2-0| = 4 ,

to obtain the value IA =4.

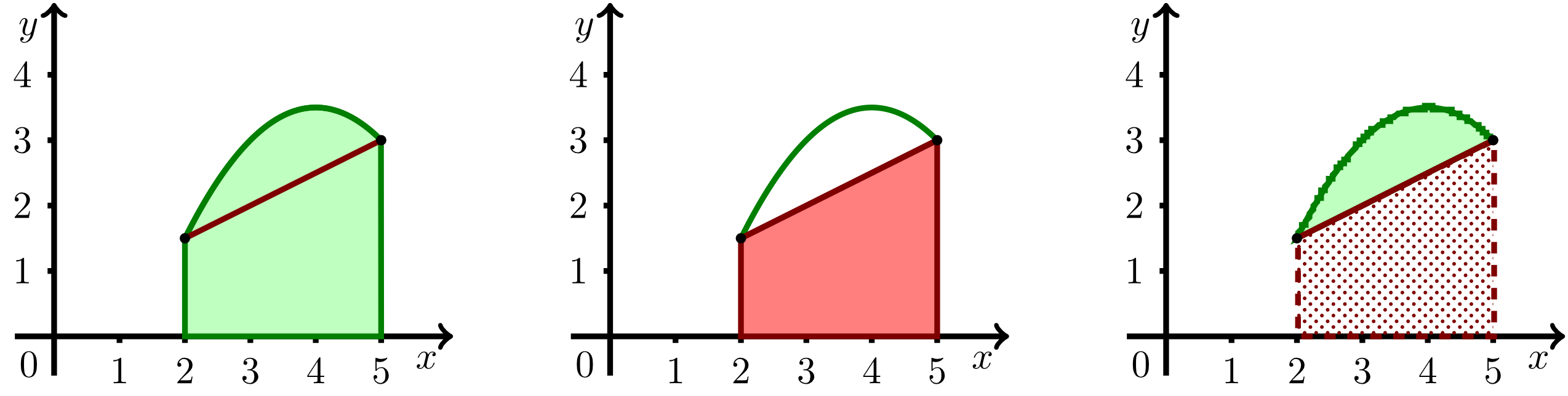
However, not only areas of regions between a graph of a function and the x-axis can be calculated but also areas of regions that are bounded by two graphs of functions as illustrated in the figure below. The right-hand part of this figure indicates the required area that is calculated as the difference of the area in the left part of the figure and the area in the middle.

Again, this principle shall first be presented formally, then explained by means of an example.
Calculation of Areas of Regions between the Graphs of two Functions 8.3.3
Let two continuous functions f,g:[a;b]→ℝ on an interval [a;b] be given. Moreover, let x1 , ..., xm be the zeros of f-g with x1 < x2 <…< xm . We set x0 :=a and xm+1 :=b.
Then the area of the region between the graphs of f and g can be calculated from

∫a b |f(x)-g(x)| dx= ∑k=0 m| ∫ xk xk+1 (f(x)-g(x)) dx| .


Let us now consider an example.
Example 8.3.4
Calculate the area IA of the region between the graphs of f and g with f(x)= x2 and g(x)=8- 1 4 x4 for x∈[-2;2].
First, we find the zeros of the function f-g. From

f(x)-g(x) = 1 4 x4 + x2 -8 = 1 4 ( x4 +4 x2 -32) = 1 4 ( x4 +4 x2 + 22 - 22 -32) = 1 4 ( ( x2 +2)2 -36)

the real zeros of f-g can be calculated:

( x2 +2)2 -36=0 ⇔ ( x2 +2)2 =36 ⇔ x2 +2=6 ⇔ x2 =4 ⇔ x=±2 .

Alternatively, from the third binomial formula, we have:

0 = ( x2 +2)2 -36= ( x2 +2)2 - 62 = ( x2 +2-6)·( x2 +2+6)=( x2 -4)·( x2 +2+6)=(x-2)·(x+2)·( x2 +8) .

In the first calculation, after taking the first root we did not consider the case x2 +2=-6 any further since the zeros obtained from the resulting equation x2 =-8 are not real. Thus, the real zeros of f-g are -2 and 2. These are also the boundary points of the interval of integration. Thus, a partition of the integral into different parts is not necessary. On the interval of integration, the function values of f are smaller than the function values of g. For the area of the region, we obtain

IA = ∫-2 2 |f(x)-g(x)|dx = ∫-2 2 (g(x)-f(x))dx = ∫-2 2 (- 1 4 x4 - x2 +8)dx = 2 ∫0 2 (- 1 4 x4 - x2 +8)dx ,       since the integrand is even = [- 1 20 x5 - 1 3 x3 +8x]0 2 = 2·(- 32 20 - 8 3 +16) = 352 15  .



: