Chapter 8 Integral Calculus
Section 8.2 Definite Integral8.2.5 Exercises
The first exercise picks up the idea (from the definition of the integral) of calculating the value of the integral based on an appropriate partition. For this purpose, in this first exercise more general shapes are used besides the standard rectangles, such as triangles.
Exercise 8.2.16
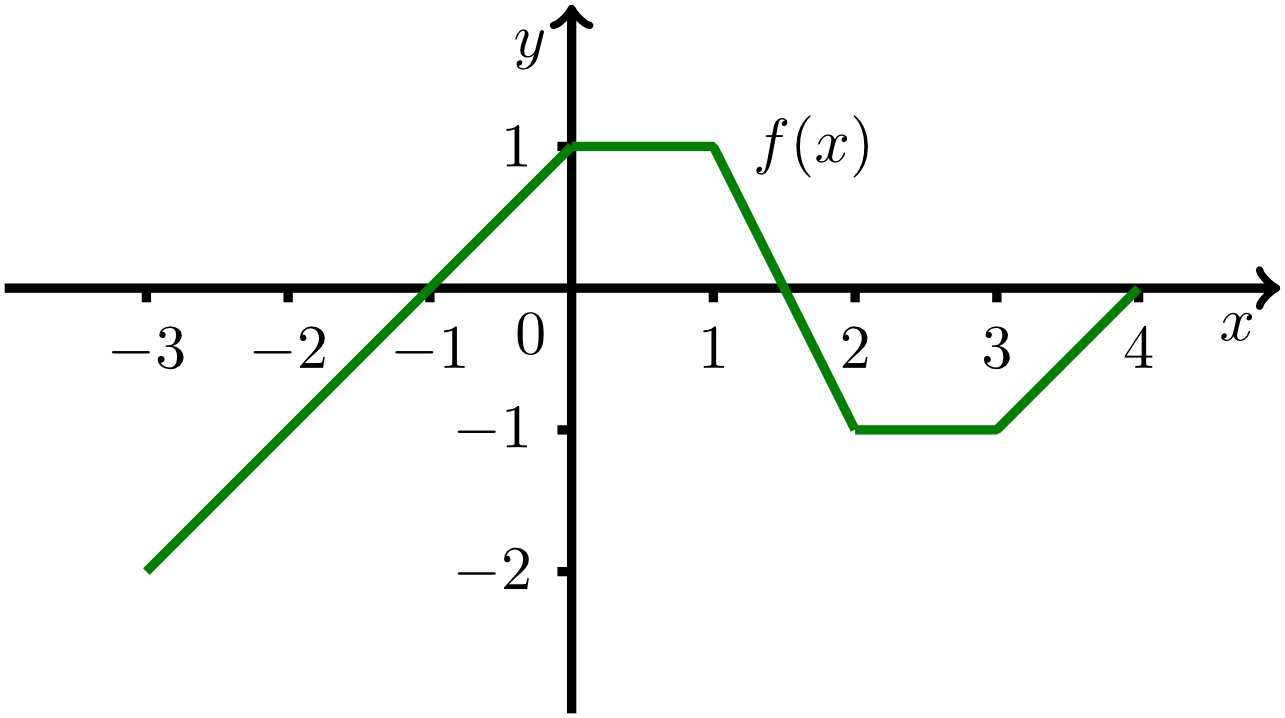
Calculate the integral of the function with the graph shown in the figure below applying methods of the elementary geometry, i.e. by subdividing the "area below the graph" into elementary geometrical shapes such as triangles or rectangles that either lie above or below the -axis. In this case, you can subsequently calculate the single areas using the formulas for triangles and rectangles.
The value of the integral is the sum of the areas of regions lying above the -axis minus the sum of the areas of regions lying below the -axis. In this sense, the value of the integral can be considered as the sum of signed areas.
The value of the integral is .
The value of the integral is the sum of the areas of regions lying above the -axis minus the sum of the areas of regions lying below the -axis. In this sense, the value of the integral can be considered as the sum of signed areas.
The value of the integral is .
Exercise 8.2.17
Calculate the following integrals:
Exercise 8.2.18
The value of the integral is
.
.
Exercise 8.2.19
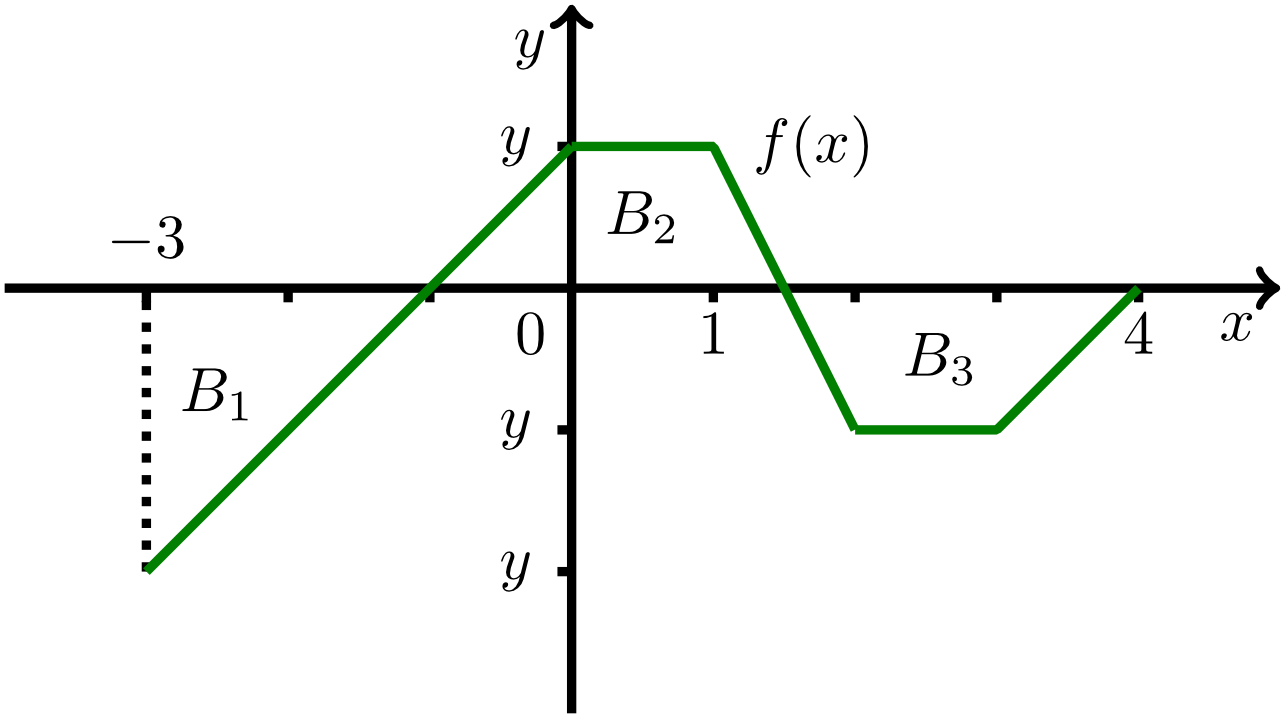
Calculate a real number such that the value of the integral
equals zero. The required value of is .
equals zero. The required value of is .
Exercise 8.2.20
Calculate the following integrals:
Exercise 8.2.21
The value of the integral is .
Exercise 8.2.22
Calculate the following integrals
Exercise 8.2.23
Calculate the integral
.
.
 Onlinebrückenkurs Mathematik
Onlinebrückenkurs Mathematik