Chapter 8 Integral Calculus

Section 8.2 Definite Integral

8.2.4 Properties of the Integral

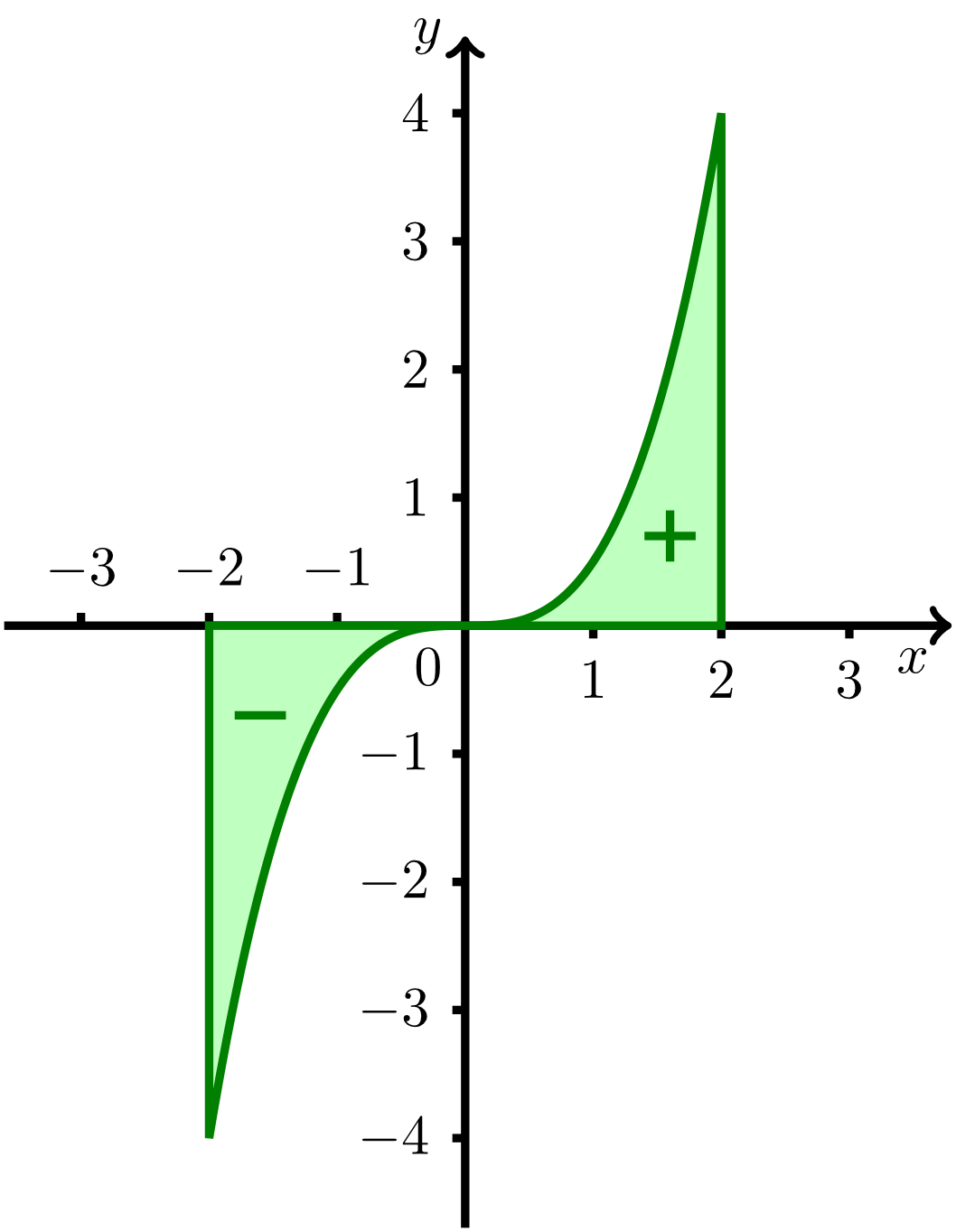
For odd functions $f:[-c;c]\to ℝ$, the integral is zero. For example, consider the function $f$ on $[-2;2]$ with $f(x)=x^3$ shown in the figure below. The graph of $f$ is subdivided into two parts, namely in a part between $-2$ and $0$ and a part between $0$ and $2$, and the two regions bounded by the graph and the $x$-axis are investigated. The two regions can be transferred into each other by a point reflection (central inversion). Both regions are equal in size. However, forming the Riemann sum of both regions, one finds that the area of the region below the $x$-axis takes a negative value. Thus, if the integrals for the two regions are added to calculate the integral over the interval from $-2$ to $2$, the area of the region above the positive $x$-axis is positive. The area of the region below the negative $x$-axis is equal in size but has a negative sign. Thus, the sum of the two areas equals zero. Thus, for odd functions $f$, we have the following rule:

${\displaystyle {\int }_{-c}^{c}f(x)\hspace{0.17em}dx=0\hspace{0.5em}.}$

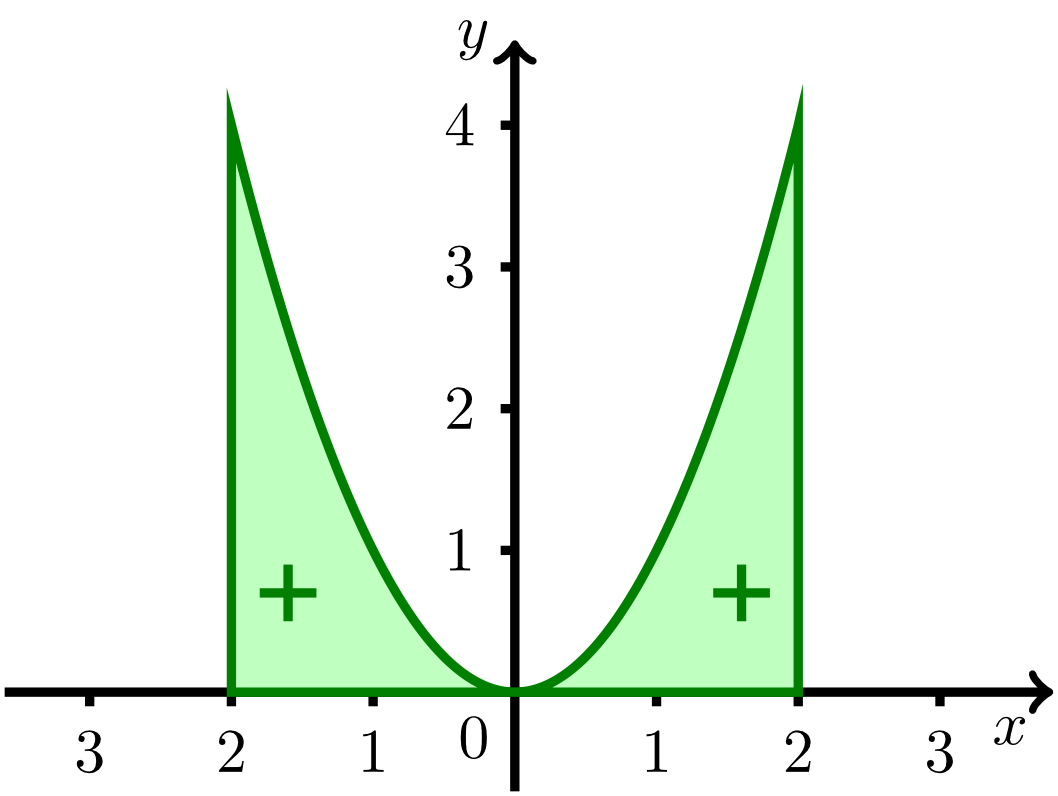
For an even function $g:[-c;c]\to ℝ$, the graph is symmetric with respect to the $y$-axis. The region between the graph of $g$ and the $x$-axis is here symmetric with respect to the $y$-axis. Thus, the region to the left of the $y$-axis is the mirror image of the region to the right. The sum of the areas of the two regions is

${\displaystyle {\int }_{-c}^{c}g(x)\hspace{0.17em}dx=2·{\int }_0^{c}g(x)\hspace{0.17em}dx\hspace{0.5em}.}$


This rule for the integral applies to every integrable function $g$ that is even, even if the function takes negative values. Due to the calculation rule above, it is then sufficient to calculate the integral for non-negative values of $x$ with the lower limit $0$ and the upper limit $c$.
Often, the calculation of an integral is easier if the integrand is first transformed into a known form. Examples of possible transformations shall be considered below. In the first example, power functions are investigated.

The next example demonstrates a transformation of an integrand involving exponential functions.

Consider a rational function. If the degree of the numerator polynomial is greater or equal to the degree of the denominator polynomial, a polynomial long division is carried out first (see Module 6). Depending on the situation, further transformations (e.g. partial fraction decomposition) may be appropriate. These can be found in advanced textbooks and formularies. In the following example, a polynomial long division is carried out to integrate a rational function.