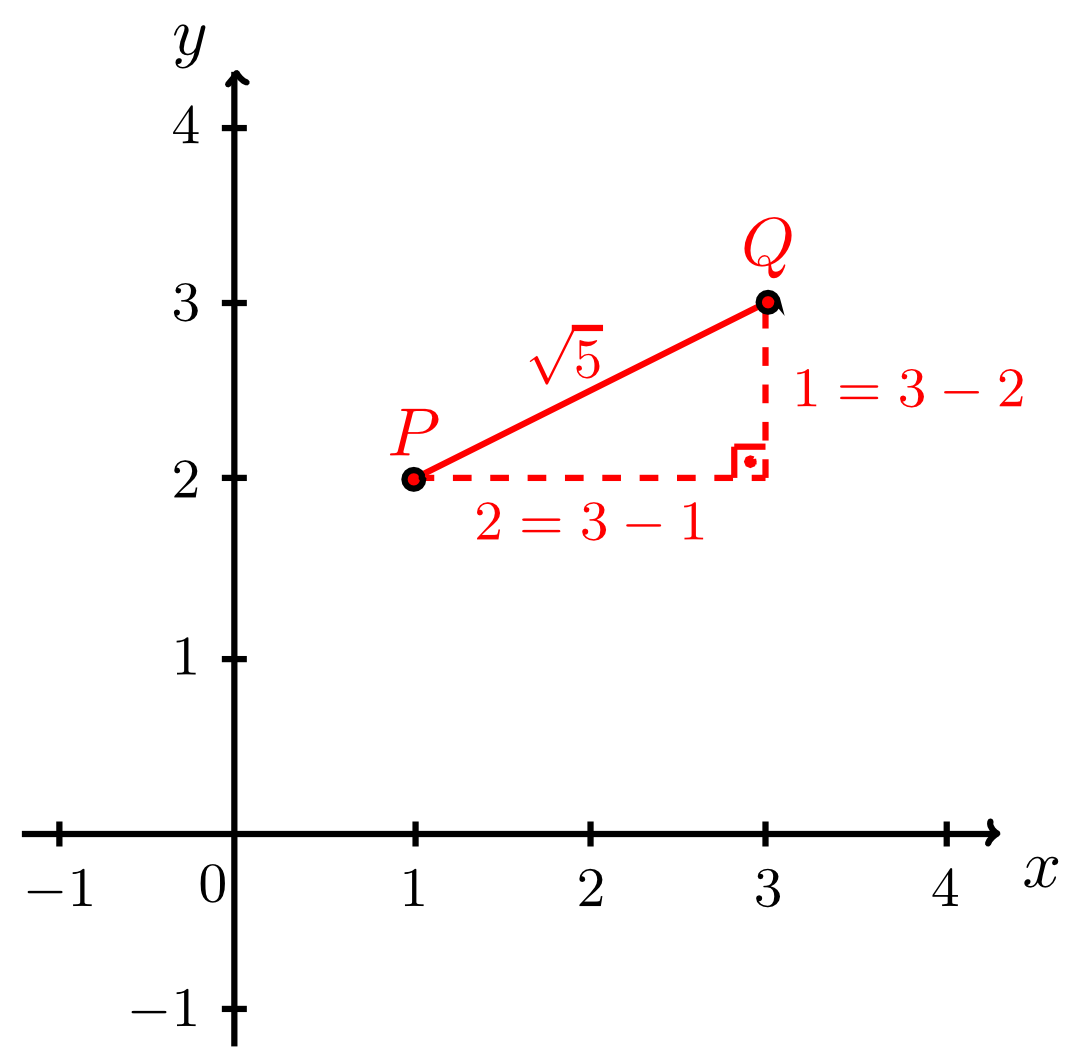Chapter 9 Objects in the Two-Dimensional Coordinate System

Section 9.3 Circles in the Plane

9.3.2 Distance and Length of a Line Segment

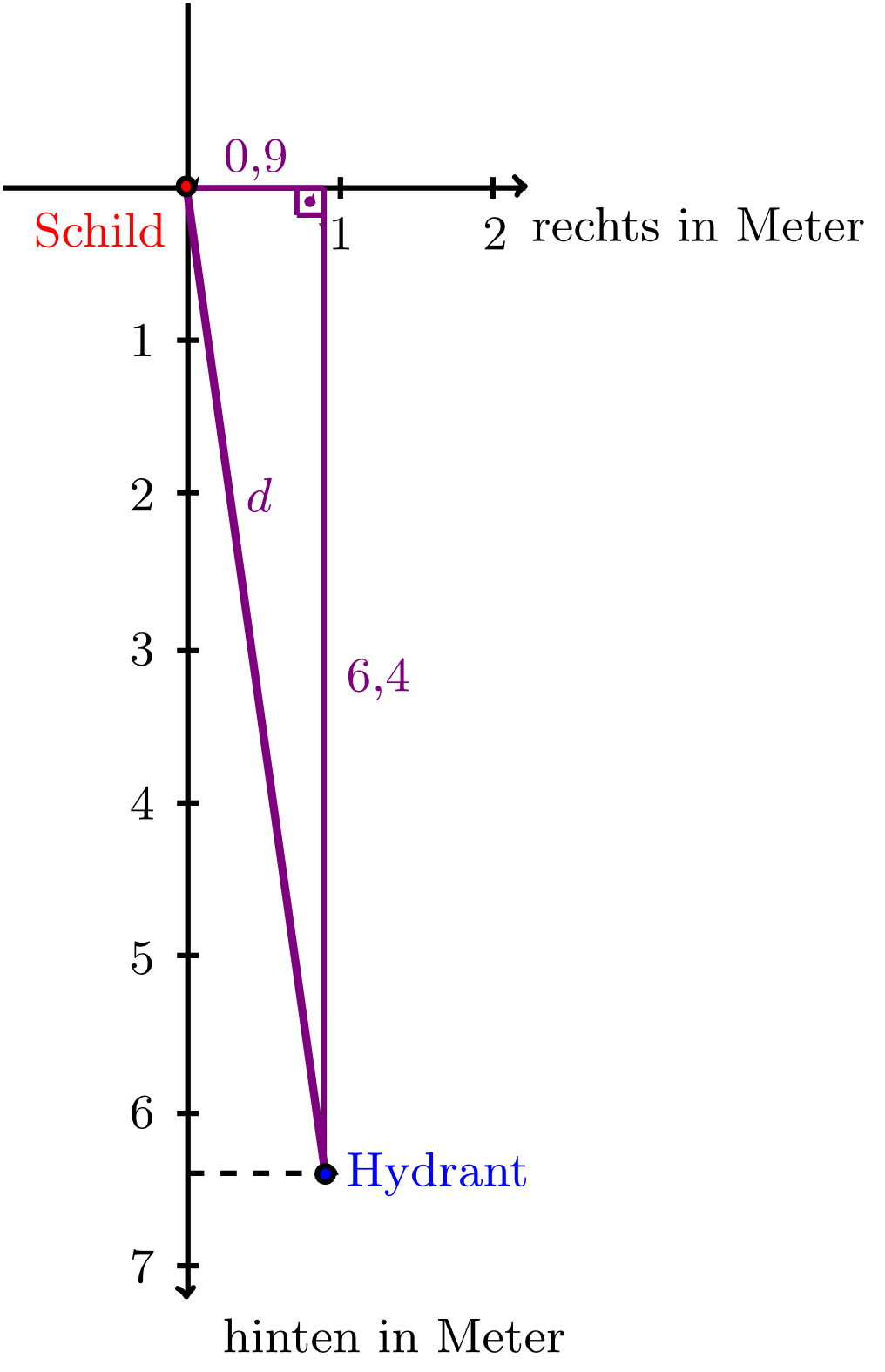
If we recall the first example of a hydrant in Section 9.1.1, we see that we are now able to specify the position of the hydrant in a coordinate system by means of the data given on the hydrant's plate. However, if we are interested in the distance of the hydrant from the plate, then we have to calculate this distance from the coordinates.

For this purpose, Pythagoras' theorem is useful:

For the distance $d$ between the plate and the hydrant, we have

${\displaystyle d^2=0.9{}^2+6.4{}^2\hspace{0.5em}.}$
Thus, the distance $d$ can be calculated (approximately):

${\displaystyle d=\sqrt{0.81+40.96}\approx 6.46\hspace{0.5em}.}$
The distance between the plate and the hydrant is (measured in the unit lengths of metres) about 6 metres and 46 centimetres. For purely mathematical purposes, the unit length is not relevant, and that we will omit it again from here onwards.
The example of the plate and the hydrant above can easily be generalised. The distance between two points in $ℝ{}^2$ can always be determined using an appropriate right triangle and Pythagoras' theorem.

Thus, the distance between two points in the plane can be calculated by determining the side lengths of a right triangle from their abscissas and ordinates and then applying Pythagoras' theorem. Furthermore, it is obvious from Example 9.3.1 above that the distance between the points $P$ and $Q$ equals the length of a finite segment of the line $PQ$, namely the segment between $P$ and $Q$. This finite segment of the line $PQ$ is called line segment between $P$ and $Q$ and is denoted by the symbol $\overline{PQ}$. The length of the line segment is the distance between $P$ and $Q$ and is denoted by the symbol $[\overline{PQ}]$.

Two points have the distance zero if they coincide.