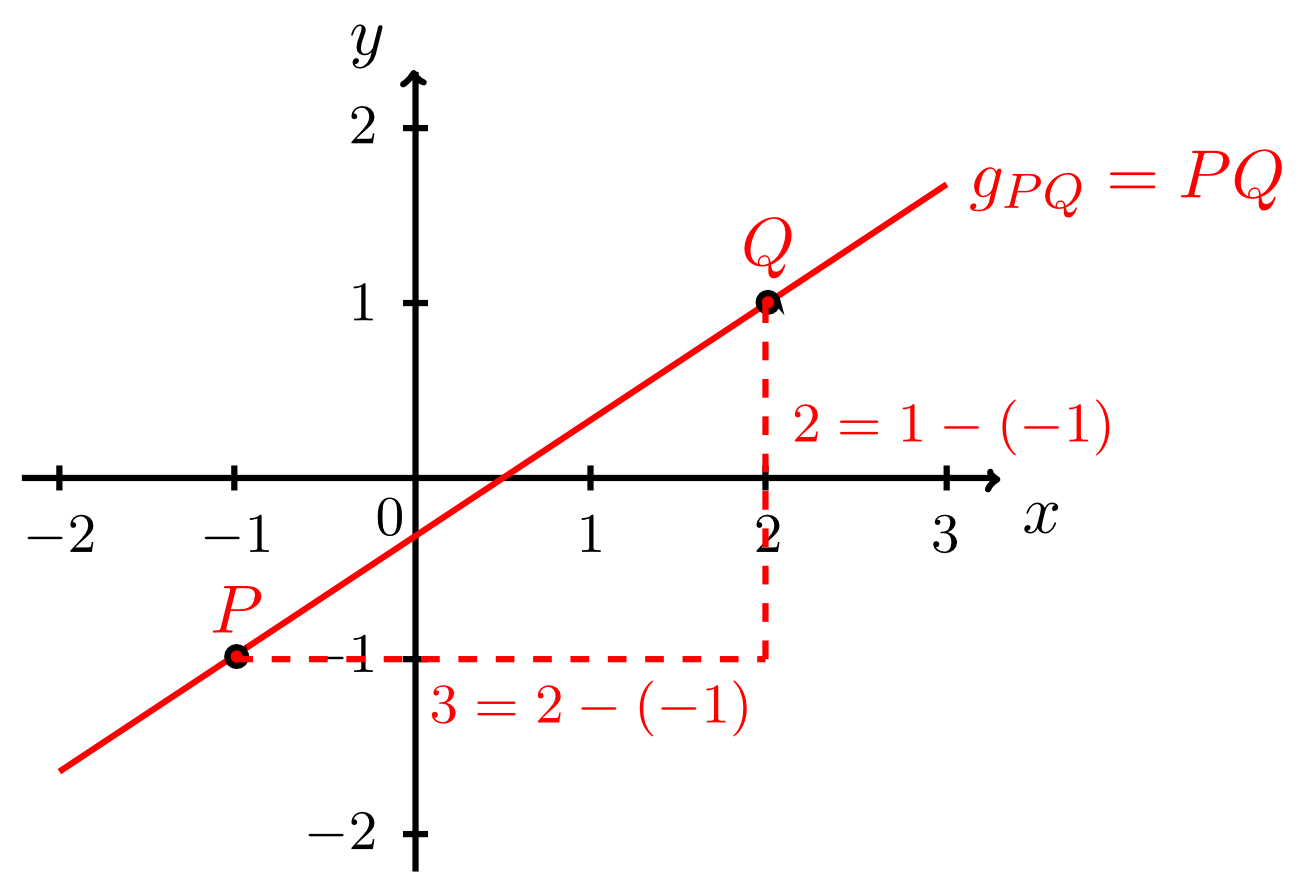Chapter 9 Objects in the Two-Dimensional Coordinate System

Section 9.2 Lines in the Plane

9.2.2 Coordinate Form of Equations of a Line

Let us first introduce the most general form of a coordinate equation of a line. Using this equation, every line in the plane can be specified as an infinite set of points with respect to a given coordinate system.

Info 9.2.2

A line

g

ℝ^{2}

is a set of points

g = {(x; y) \in ℝ^{2} : p x + q y = c} .

Here,

p

q

c

are real numbers that define the line. At least one of the numbers

p

and

q

must be non-zero. The linear equation

p x + q y = c

is called the equation of a line or, more specifically, to distinguish it from other forms of equations of a line, as coordinate form of the equation of a line. A common abbreviation for the explicit set notation given above is to specify only the variable of the line and the equation of the line:

g : p x + q y = c .

The example below shows a few lines and their set notations or equations.

Example 9.2.3

$g = {(x; y) \in ℝ^{2} : x - y = 0}$

Here, we have $p = 1$ , $q = - 1$ , and $c = 0$ .
$h : - x - 2 = - 3 y \Leftrightarrow h : - x + 3 y = 2$

Here, we have $p = - 1$ , $q = 3$ , and $c = 2$ .
$α : 4 y = 1$

Here, we have $p = 0$ , $q = 4$ , and $c = 1$ .
$β = {(x; y) \in ℝ^{2} : x - 1 = 0}$

Here, we have $p = 1$ , $q = 0$ , and $c = 1$ .

Now we want to be able to draw a line correctly in a coordinate system in

ℝ^{2}

. The line can be uniquely defined by an equation of a line, or by other data. To do this, we have to establish a relation to the graphs of linear affine functions. We also need to know by what kind of data a line in the plane is uniquely defined. This information will be given below.

Info 9.2.4

A line

g

given by an equation of a line in coordinate form

g : p x + q y = c

can be converted into normal form if

q \neq 0

. In this case, the equation of a line

p x + q y = c

can be solved for

y

, and the normal form of

g

is then

g : y = - \frac{p}{q} x + \frac{c}{q} .

In this form, the line describes a graph of a linear affine function

f

with the slope

- \frac{p}{q}

and the

y

-intercept

\frac{c}{q}

f : {\begin{matrix} ℝ & \to & ℝ \\ x & ⟼ & y = f (x) = - \frac{p}{q} x + \frac{c}{q} . \end{matrix}

Since the slope and the

y

-intercept can be read off from the equation of a line in normal form, lines can be drawn in the same way as the graphs of linear affine functions.

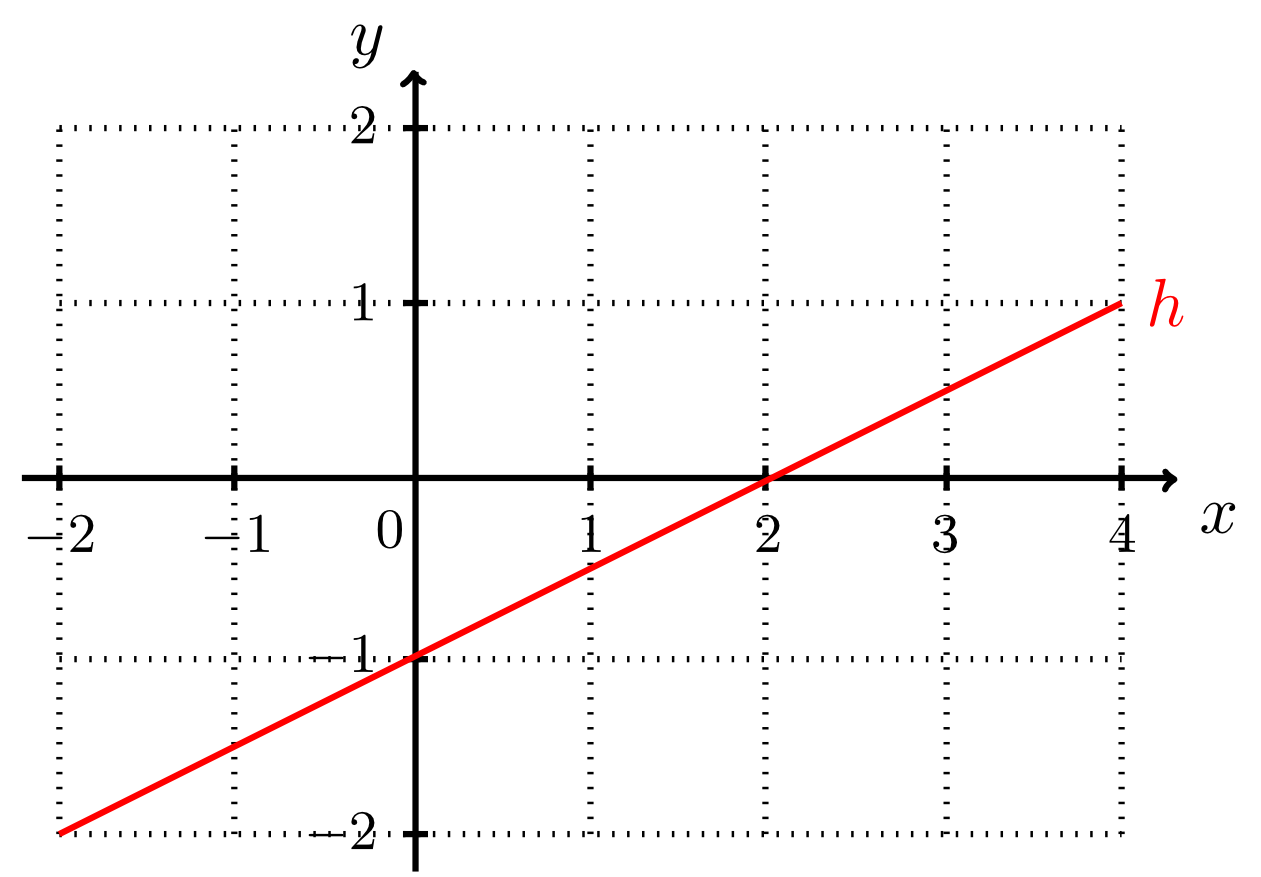
Example 9.2.5

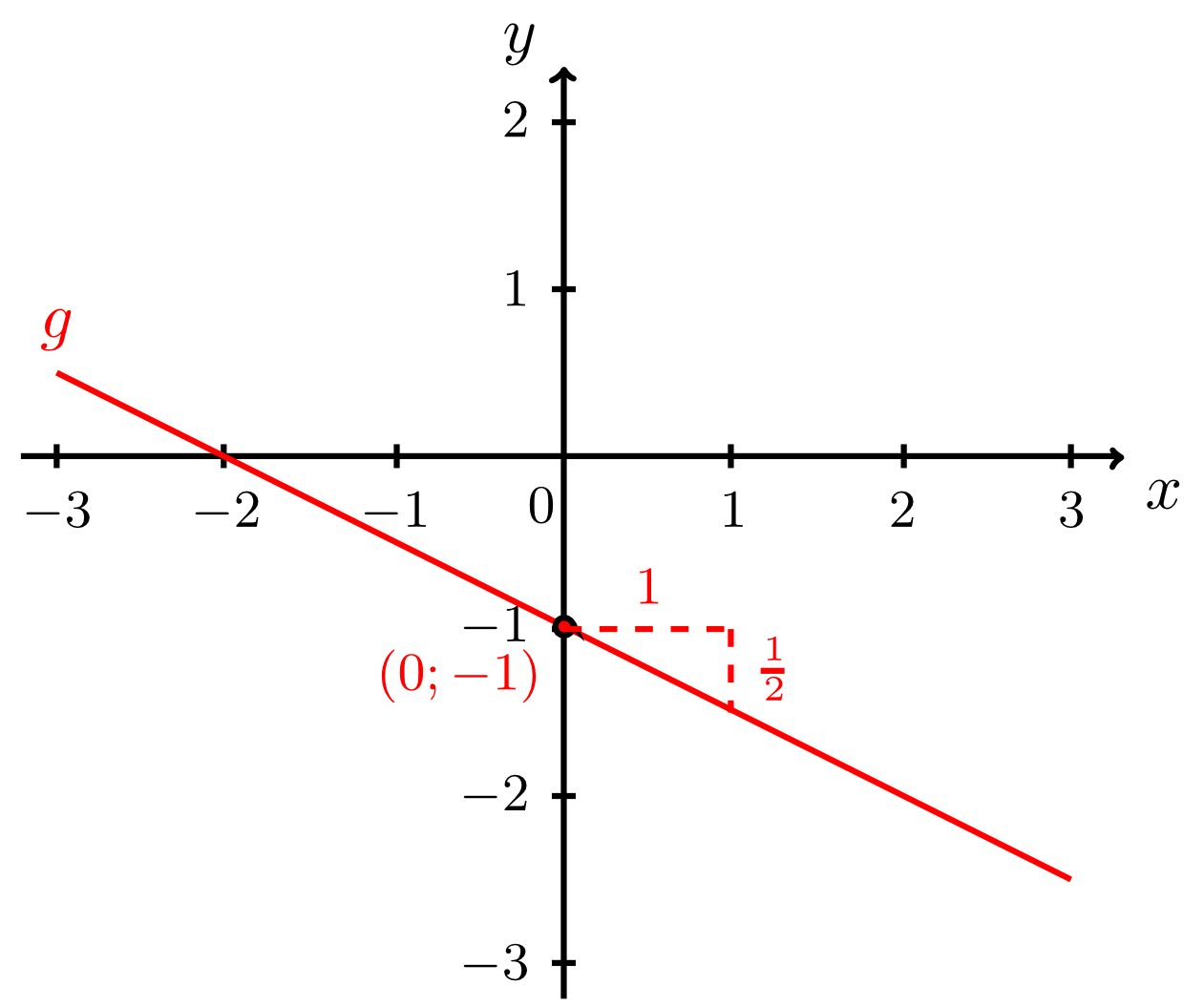
The line

g = {(x; y) \in ℝ^{2} : - x - 2 y = 2}

has the equation

- x - 2 y = 2

in coordinate form. This equation can be converted into the form

y = - \frac{1}{2} x - 1

by equivalent transformations of linear equations. Thus, the line

g

has the normal form

g : y = - \frac{1}{2} x - 1,

and it describes the graph of the linear affine function

f : {\begin{matrix} ℝ & \to & ℝ \\ x & ⟼ & y = f (x) = - \frac{1}{2} x - 1 \end{matrix}

with the slope

- \frac{1}{2}

and the

y

-intercept

- 1

.
To draw

g

one has to understand the following: the

y

-intercept

- 1

implies that the point

(0; - 1)

lies on

g

. Starting from this point, the line

g

can be drawn correctly by constructing a slope triangle of slope

- \frac{1}{2}

(by

x = 1

units to the right and by

y = \frac{1}{2}

units downwards) in the correct direction:

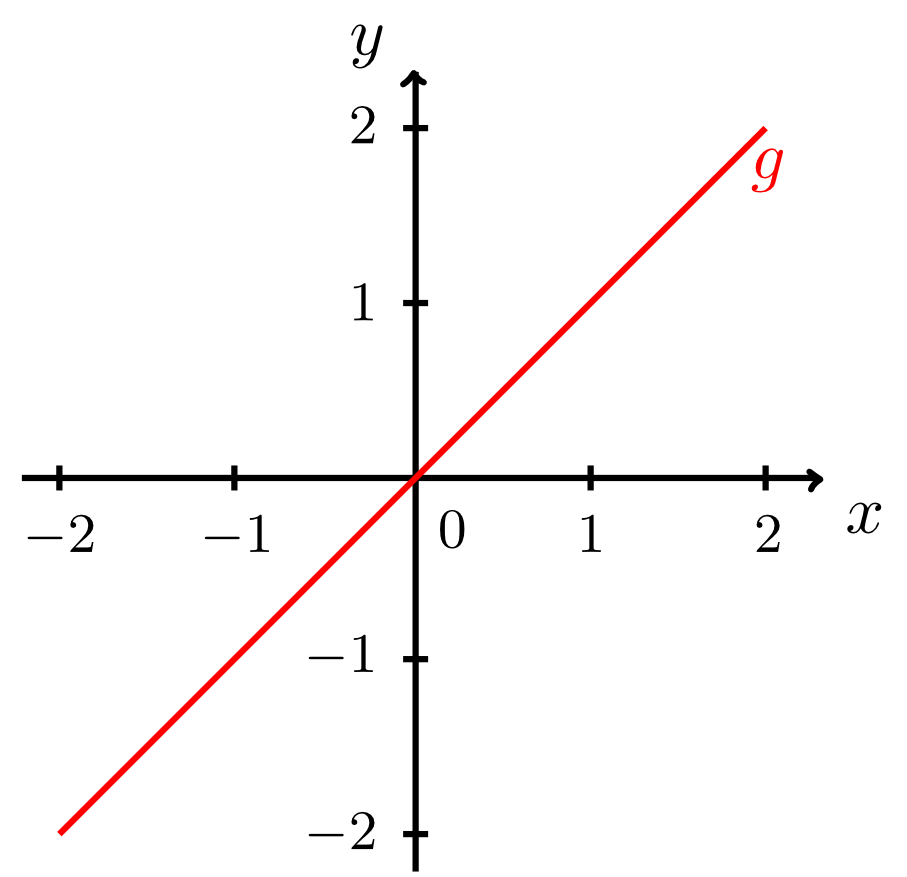
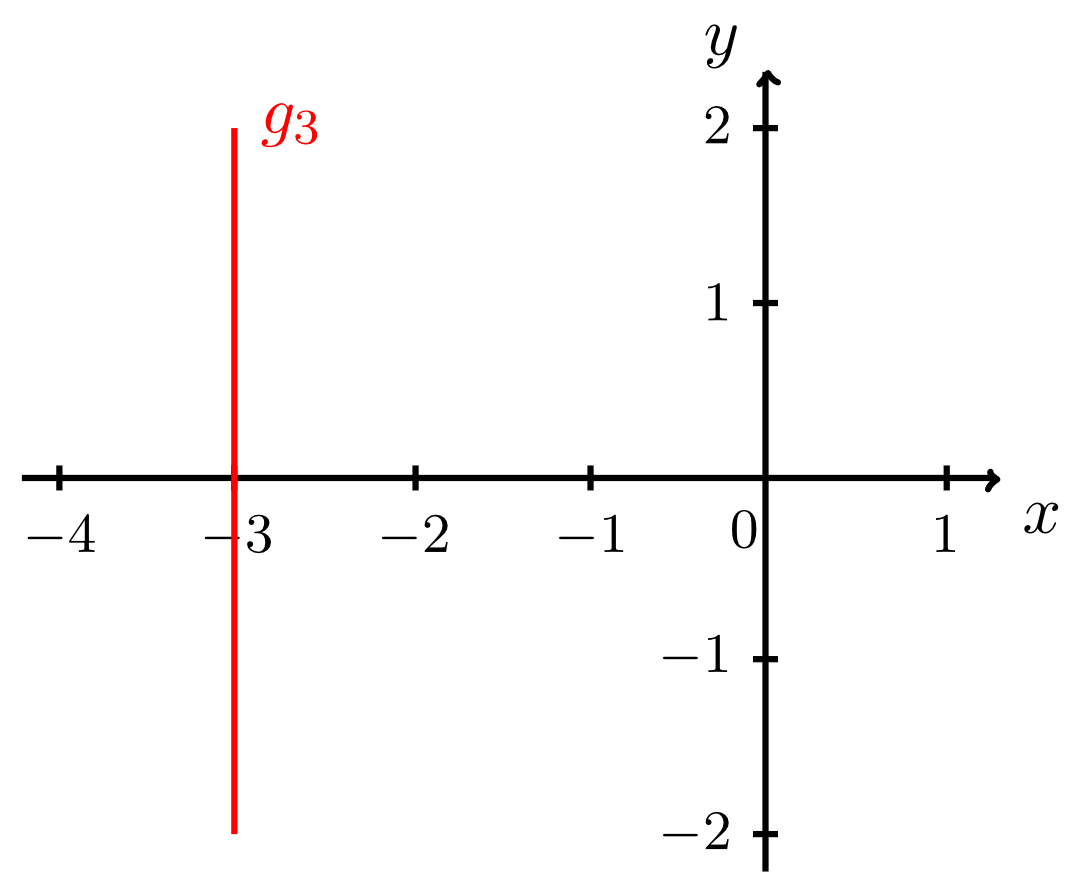
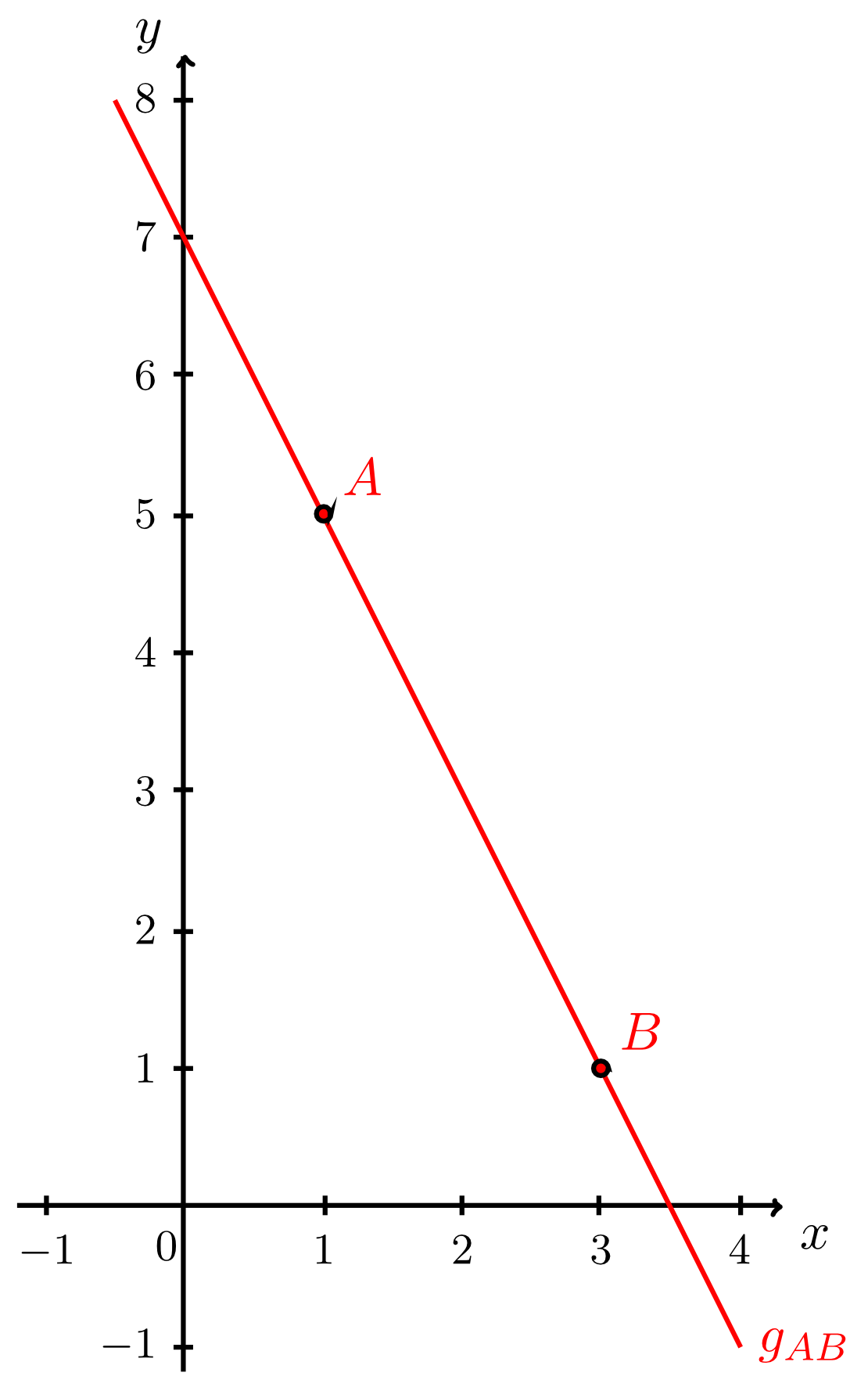
There two special cases: they can be demonstrated by the two lines

α : 4 y = 1

and

β : x - 1 = 0

in Example 9.2.3 (see figure below).

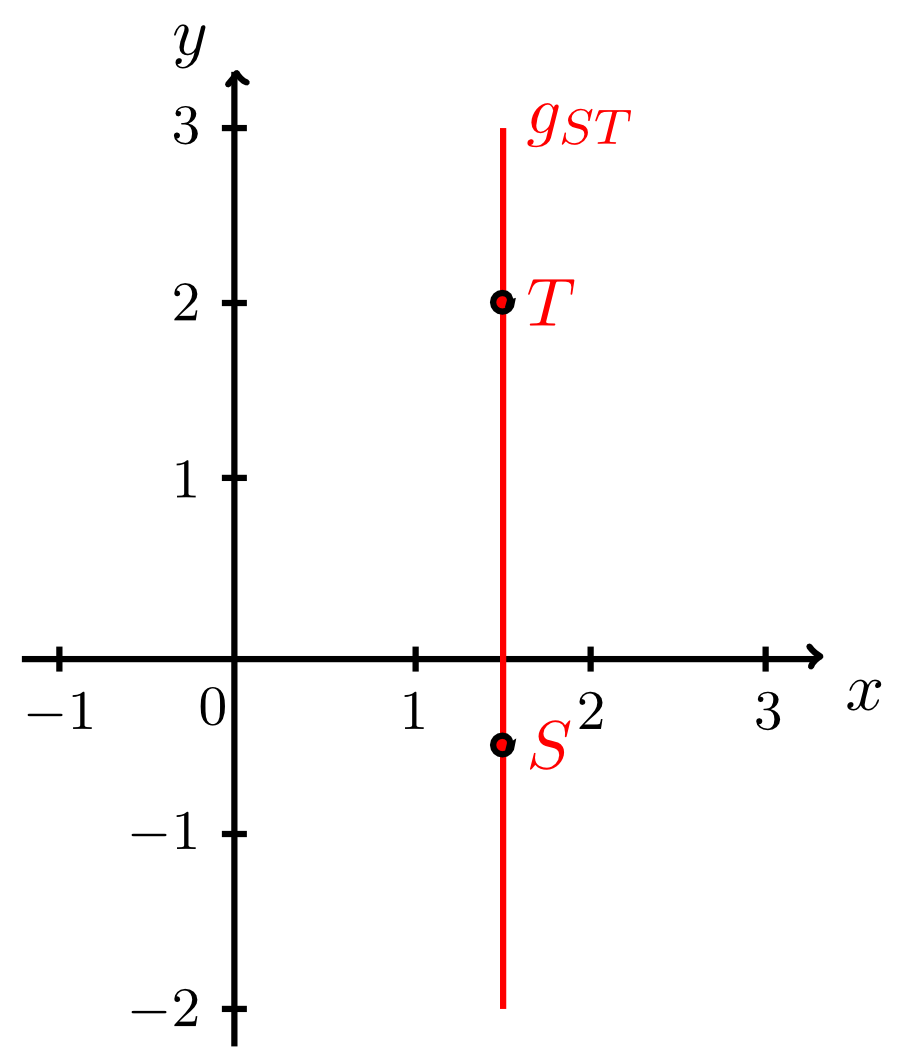
The line

α

is parallel to the

x

-axis. Thus, its normal form

α : y = \frac{1}{4}

describes the graph of a constant function as a special case of the linear affine functions. The line

β

is parallel to the

y

-axis. Its equation of a line cannot be converted into normal form since

q = 0

. This is true for all lines that are parallel to the

y

-axis.For such lines a normal form does not exist, since these lines cannot be a graph of a function (as discussed in Section 6.1.4). Lines that are parallel to the

y

-axis have neither have a

y

-intercept (since they do not intersect the

y

-axis) nor a slope. However, for the sake of consistency, they can be assigned a slope of

\infty

Exercise 9.2.6

Draw the following lines in a coordinate system. Convert the corresponding equation of a line (if required and possible) into normal form first.

$g_{1} : y = - 2 x + 3$
$g_{2} : - 2 x + y - 2 = 0$
$g_{3} : x + 3 = 0$

The equation of the line is given in normal form, so no transformation is required.
The normal form of the line is $g_{2} : y = 2 x + 2$ .
The equation of the line cannot be converted into normal form. The line is parallel to the $y$ -axis.

Exercise 9.2.7

Let a line

h

be given by the figure below.

Specify the equation of the line

h

in normal form.

h : y =

The equation of a line of

h

in normal form is

y = \frac{1}{2} x - 1 = 0.5 \cdot x - 1

As well as by an equations, a line in the plane can also be uniquely defined by other data. From these data, the corresponding equation of a line can be derived, and the line can be drawn in a coordinate system.

Info 9.2.8

There are two alternative ways to uniquely define a line in the plane:

"A line is uniquely defined by two points" If two points $P$ and $Q$ in $ℝ^{2}$ are given, there exists exactly one line $g$ that passes through the points $P$ and $Q$ . The line passing through $P$ and $Q$ is then also denoted by $g = g_{P Q} = g_{Q P}$ or simply by $g = P Q$ .
"A line is uniquely defined by a point and a slope" If a point $P$ in $ℝ^{2}$ and a slope $m$ are given, there exists exactly one line $g$ that passes through $P$ and has the slope $m$ .

The two following examples illustrate how the equation of a line can be derived from the data that uniquely define this line, and how this line can be drawn.

Example 9.2.9

Let the points

P = (- 1; - 1)

and

Q = (2; 1)

be given. The line

g_{P Q} = P Q

passing through these two points can be drawn immediately. To determine the line of equation it is useful to construct a slope triangle from the two given points:

From the

x

-coordinates

- 1

and

2

P

and

Q

we obtain the width

3

of the slope triangle. From the corresponding

y

-coordinates

- 1

and

1

we obtain its height

2

. Thus, the slope in the equation of the line is

m = \frac{2}{3}

. For the normal form of the equation of the line

g_{P Q}

we thus obtain:

g_{P Q} : y = m x + b = \frac{2}{3} x + b .

Now, only the

y

-intercept

b

has to be determined. We know that the line

g_{P Q}

passes through the two points

P

and

Q

. Therefore, we can substitute the

x

- and

y

-coordinates of one of these points into the equation of the line, and calculate

b

. Substituting, for example, the coordinates of the point

Q = (2; 1)

results in

1 = \frac{2}{3} \cdot 2 + b \Leftrightarrow b = 1 - \frac{4}{3} = - \frac{1}{3} .

Using the point

P = (- 1; - 1)

would result in the same equation. Thus, the required equation of the line in normal form is

g_{P Q} : y = \frac{2}{3} x - \frac{1}{3} .

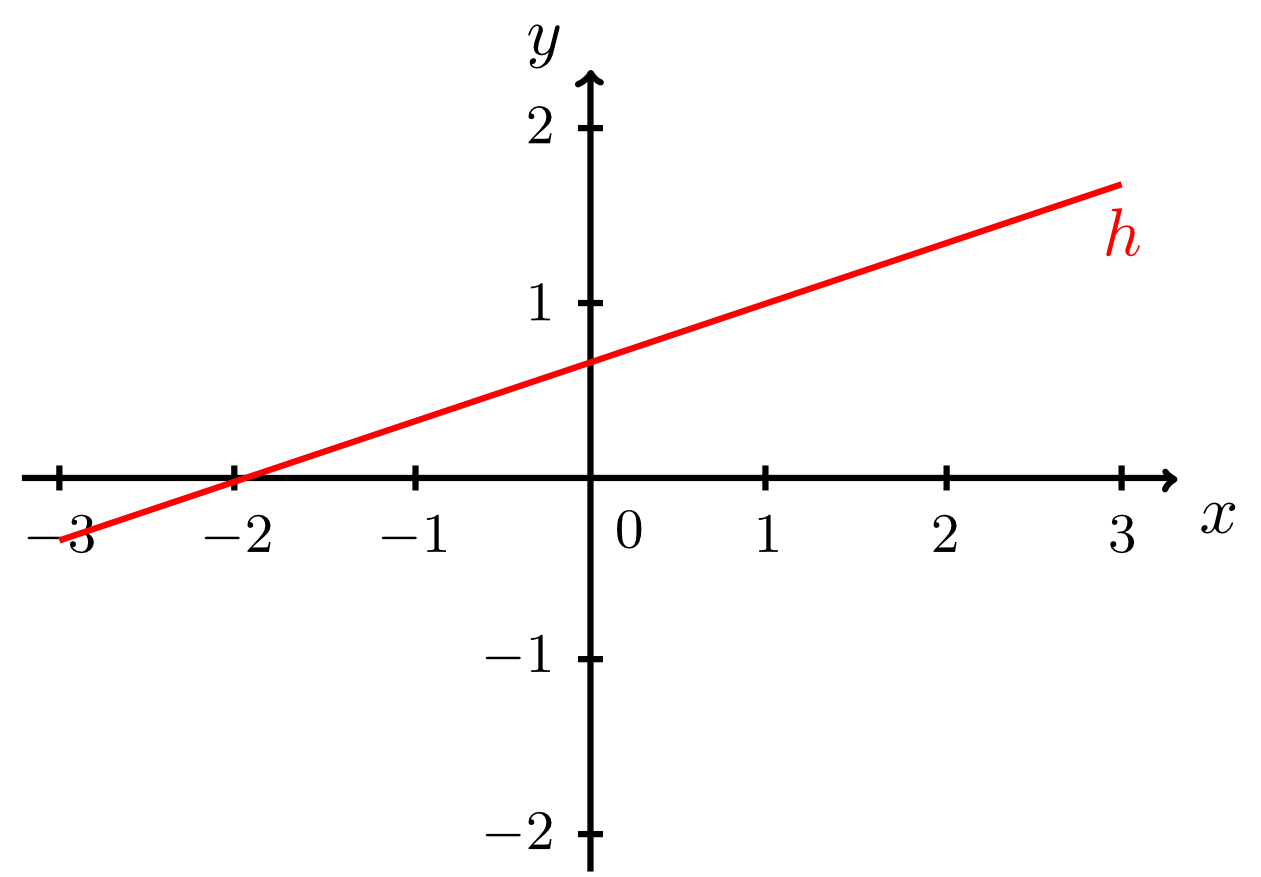
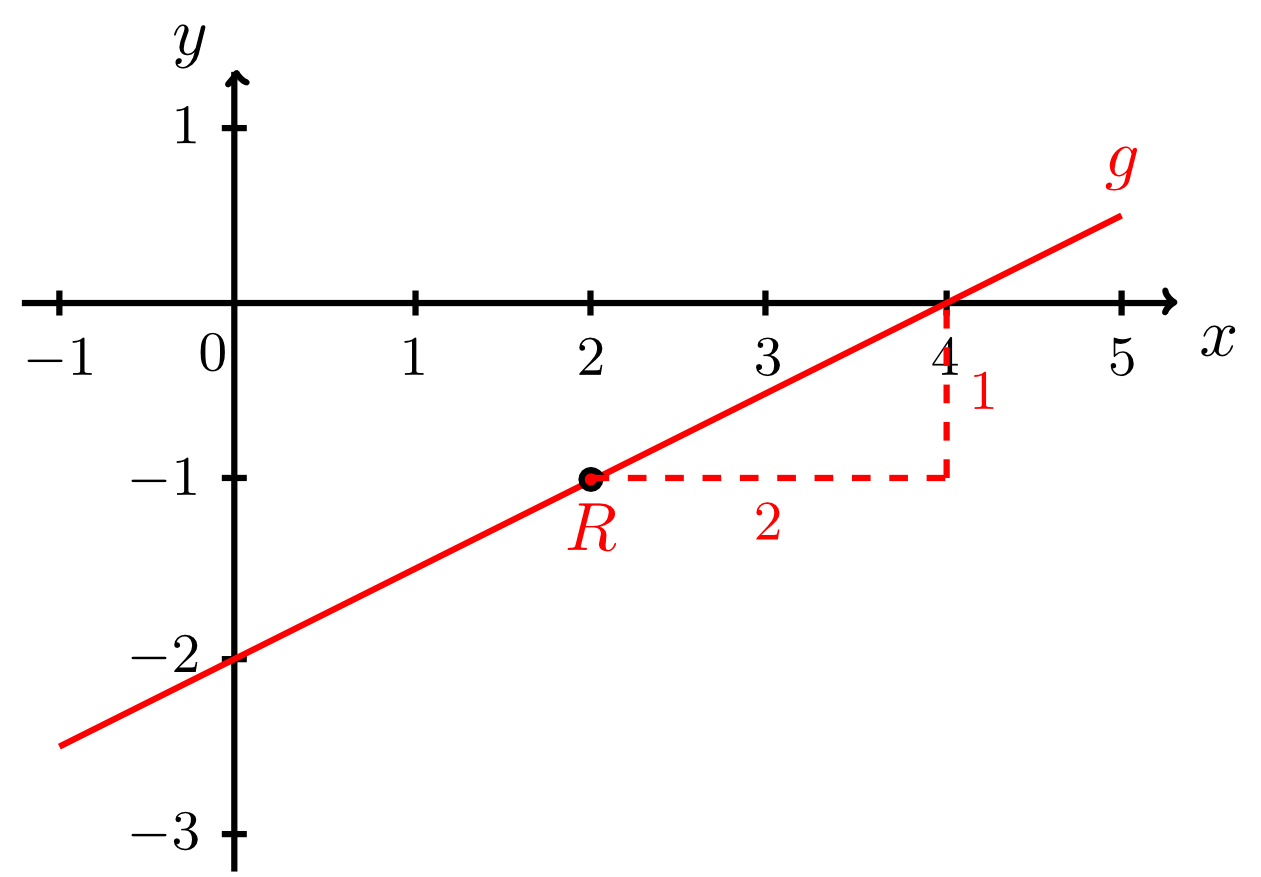
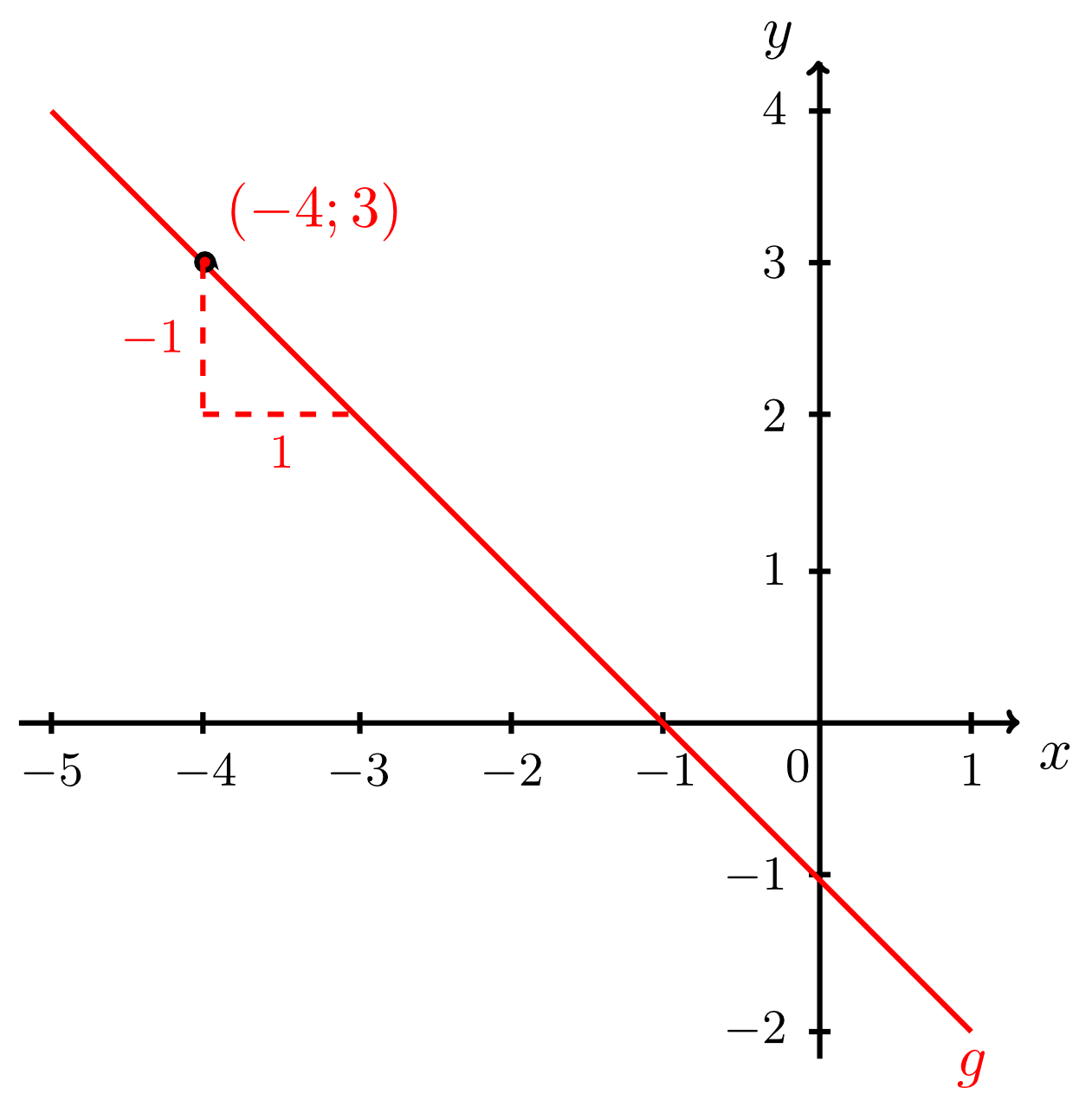
Example 9.2.10

Let the point

R = (2; - 1)

and the slope

m = \frac{1}{2}

be given. Find the line

g

that passes through the point

R

and has the slope

m = \frac{1}{2}

. As in Example 9.2.9, the equation of the line

g

in normal form can be specified immediately while the

y

-intercept is still unknown:

g : y = m x + b = \frac{1}{2} x + b .

Moreover, both the coordinates

x

and

y

of the point

R

are given here from which the

y

-intercept can be calculated, as in Example 9.2.9:

- 1 = \frac{1}{2} \cdot 2 + b \Leftrightarrow b = - 2 .

Thus, the required equation of the line is

g : y = m x + b = \frac{1}{2} x - 2 .

Using the point

R = (2; - 1)

and the slope

m = \frac{1}{2}

, the line

g

can also be drawn immediately as illustrated by the figure below.

Exercise 9.2.11

Every set of data given here defines a unique line. For each one, give the equation of the line and then sketch it.

The points $A = (1; 5)$ and $B = (3; 1)$ are on the line.
$g_{A B} : y =$
The points $S = (1.5; - 0.5)$ and $T = (\frac{3}{2}; 2)$ are on the line.
$g_{S T} : x =$
The line $g$ passes trough the point $(- 4; 3)$ with a slope of $- 1$ .
$g : y =$
The line $h$ passes trough the point $(42; 2)$ with a slope of $0$ .
$h : y =$

$g_{A B} : y = - 2 x + 7$
$g_{S T} : x = \frac{3}{2}$
$g : y = - x - 1$
$h : y = 2$

Onlinebrückenkurs Mathematik

1. Elementary Arithmetic

2. Equations in one Variable

3. Inequalities in one Variable

4. System of Linear Equations

5. Geometry

6. Elementary Functions

7. Differential Calculus

8. Integral Calculus

9. Objects in the Two-Dimensional Coordinate System

10. Basic Concepts of Descriptive Vector Geometry

11. Language of Descriptive Statistics

Chapter 9 Objects in the Two-Dimensional Coordinate System

9.2.2 Coordinate Form of Equations of a Line

Info 9.2.2

Example 9.2.3

Info 9.2.4

Example 9.2.5

Exercise 9.2.6

Exercise 9.2.7

Info 9.2.8

Example 9.2.9

Example 9.2.10

Exercise 9.2.11