Kapitel 4 Lineare Gleichungssysteme
Abschnitt 4.3 LGS mit drei Unbekannten4.3.2 Lösbarkeit und Gleichsetzmethode, Graphische Interpretation
Im Falle von Systemen aus zwei linearen Gleichungen in zwei Unbekannten kann man - wie in 4.2 gesehen - die Frage nach Lösbarkeit und Lösung des Systems sehr schön anschaulich in die Frage nach Existenz und Lage des Schnittpunkts zweier Geraden übersetzen. Und natürlich sollte man sich überlegen, ob für Systeme aus drei linearen Gleichungen in drei Unbekannten eine ähnlich bildhafte Interpretation gegeben werden kann.Erweitert man den bisherigen Raum ( und ) um eine weitere Dimension oder Variable, nämlich , dann kann man mit einer linearen Gleichung dieser drei Variablen,
eine Ebene in Koordinatenform darstellen, ganz analog zu den Geradengleichungen, die bisher untersucht wurden. Für kann diese Gleichung nach aufgelöst werden,
sodass die explizite Form der Gleichung ebenjener Ebene resultiert. Die letzte Gleichung besagt, dass jedem Paar , also jedem Punkt der --Koordinatenebene, gemäß der Vorschrift der rechten Seite ein Wert , also gewissermaßen eine Höhe, zugeordnet wird; dadurch entsteht eine Fläche über der --Ebene, die aufgrund der Linearität der Gleichung selbst eine Ebene ist.
Nun muss aber nicht nur die erste Gleichung im System 4.3.2 gelten, sondern es müssen gleichzeitig auch die zweite und die dritte Gleichung erfüllt sein, die bildlich ebenfalls als Ebenen interpretiert werden können. Wonach also bei der Suche nach Lösungen eines Systems aus drei linearen Gleichungen in drei Unbekannten gefahndet wird, ist - in der anschaulichen Sprache - das Schnittverhalten dreier Ebenen. Hierzu wird zunächst ein Beispiel betrachtet:
Beispiel 4.3.3
Es wird nach der Lösungsmenge des Linearen Gleichungssystems
gesucht; als Grundmenge wählt man die Menge der reellen Zahlen .
Jede der drei linearen Gleichungen lässt sich problemlos nach umstellen:
Setzt man jetzt die rechten Seiten der Gleichungen und gleich, so bedeutet dies - anschaulich gesprochen -, dass man die Schnittgerade der beiden durch diese Gleichungen beschriebenen Ebenen bestimmt:
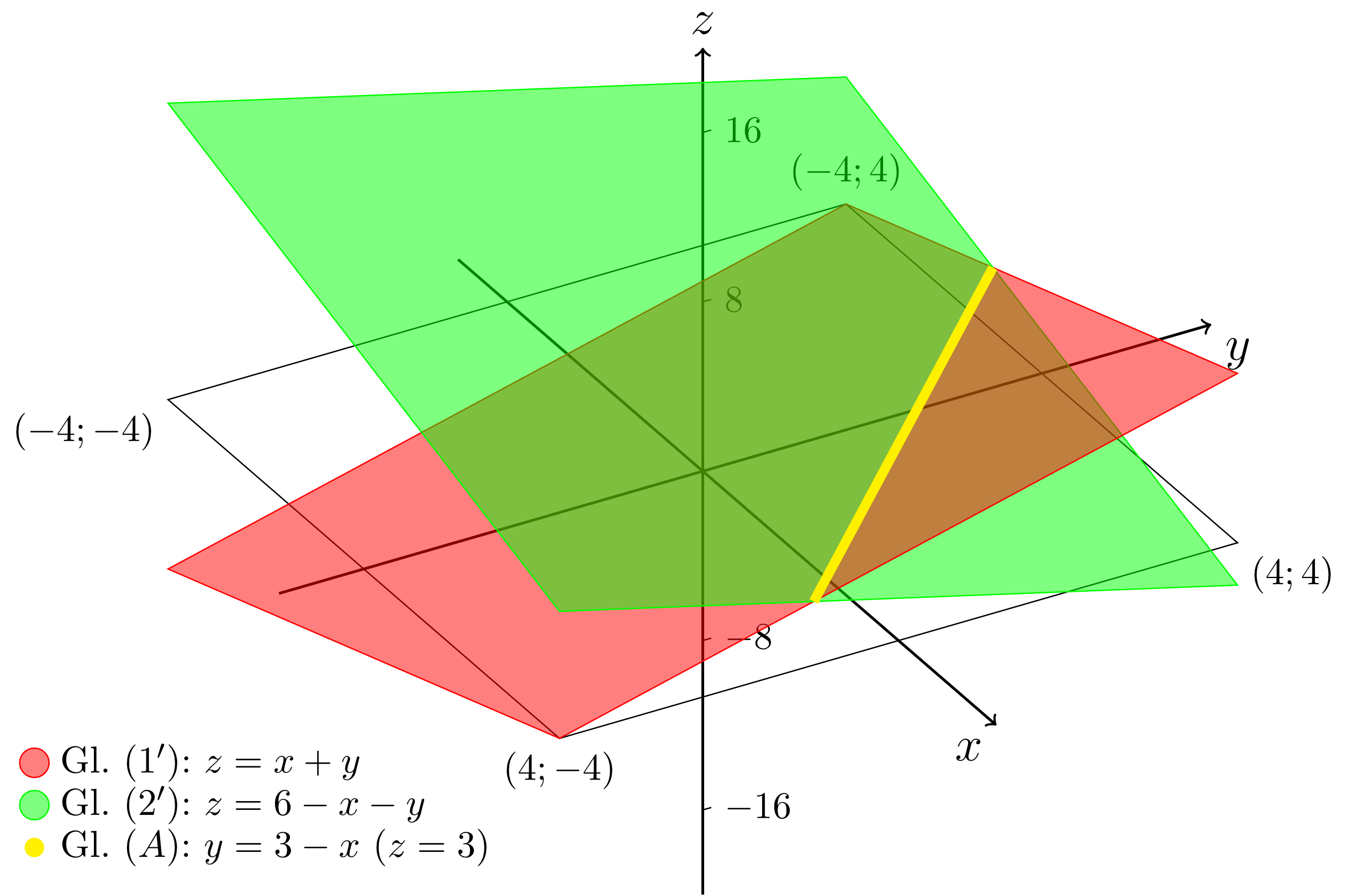
Durch Einsetzen dieser Beziehung in Gleichung oder erhält man die zugehörigen -Koordinaten der Schnittgeraden; hier ergibt sich . Die folgende perspektivische Skizze zeigt diese Schnittgerade, Gleichung , als den Schnitt der durch die Gleichungen und beschriebenen, nicht parallelen Ebenen: Die vollkommen analoge Aussage gilt, falls man die rechten Seiten von Gleichung und gleichsetzt; man erhält dann die Schnittgerade der Ebenen und :
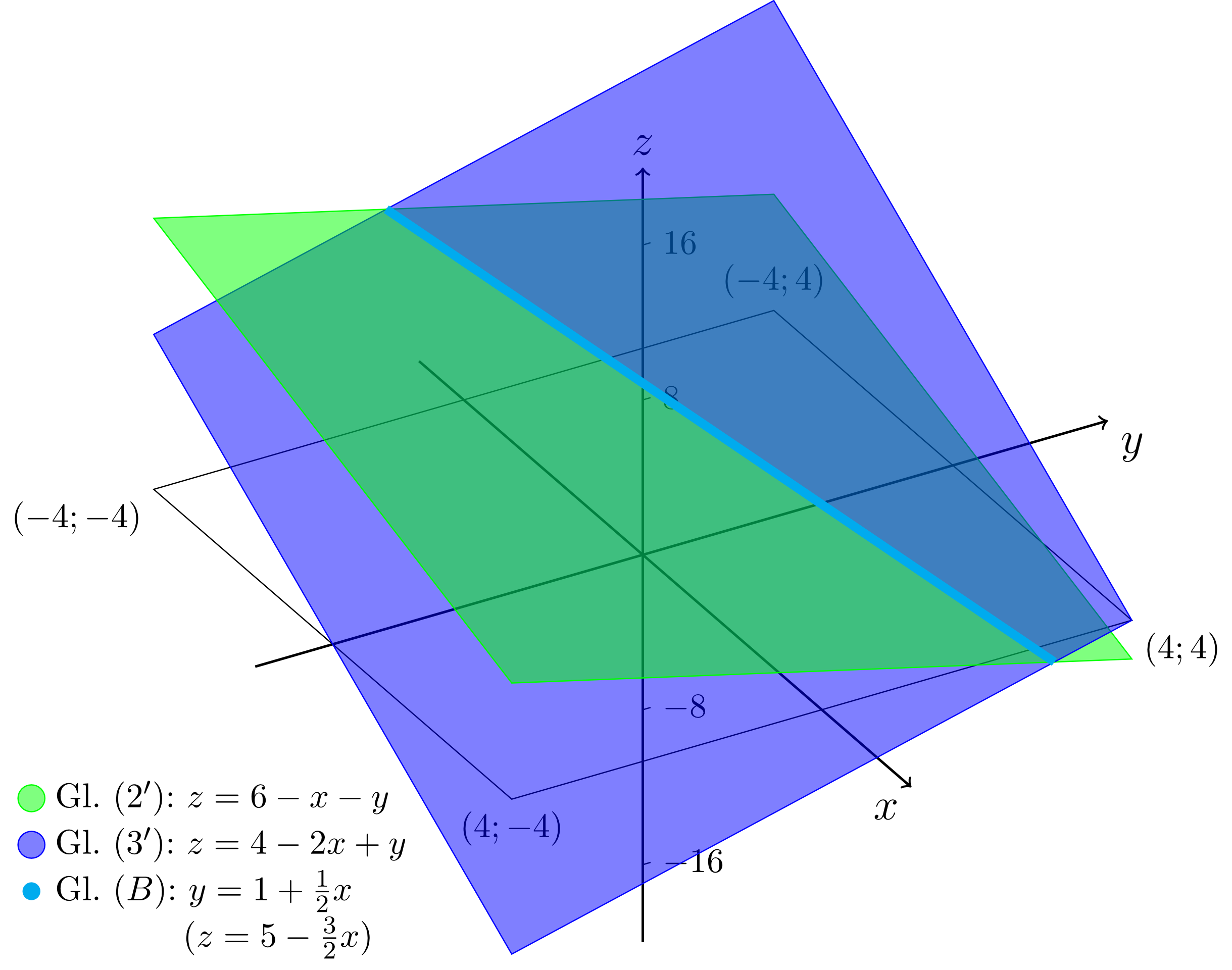
Deren -Koordinaten ergeben sich entsprechend durch Einsetzen dieser Beziehung in Gleichung oder zu . Eine diesem Sachverhalt entsprechende perspektivische Skizze aus derselben Blickrichtung zeigt diese Schnittgerade, Gleichung , als den Schnitt der durch die Gleichungen und beschriebenen, nicht parallelen Ebenen: Da im Ausgangssystem alle drei Gleichungen simultan gelten sollen, müssen auch die zwei gerade hergeleiteten Geradengleichungen gleichzeitig erfüllt sein. Im bildlichen Kontext suchen man daher den Schnittpunkt dieser beiden Geraden; diesen Schnittpunkt bekommt man, indem man die rechten Seiten der Gleichungen und gleichsetzt:
Den Lösungswert für kann man durch Einsetzen des Ergebnisses für z.B. in Gleichung berechnen:
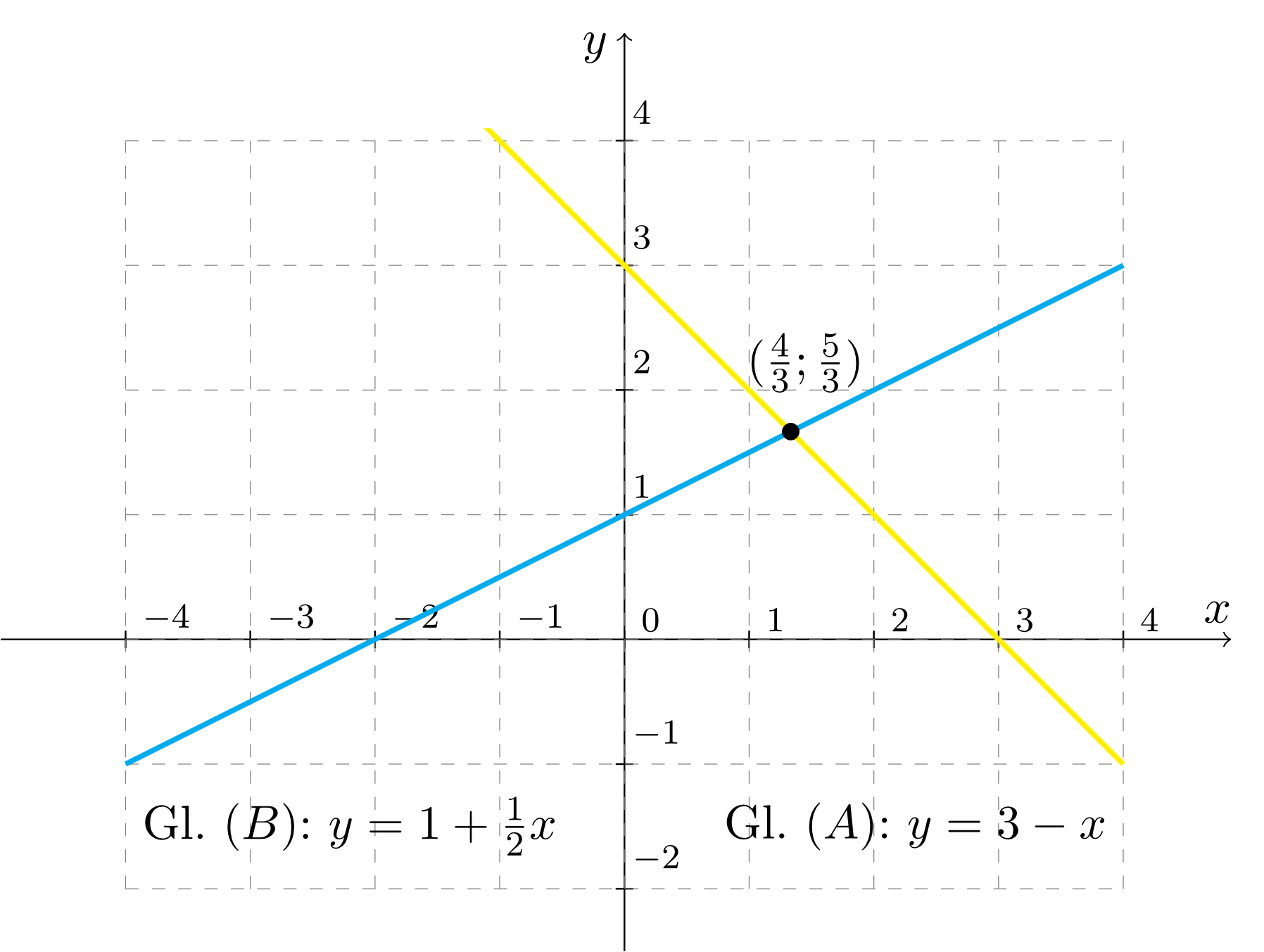
Die folgende Skizze zeigt die Schnittgeraden, Gleichungen und , in der --Ebene, Projektion - Ansicht von oben -, und deren Schnittpunkt: Der Wert für schließlich resultiert, indem man die Werte für und z.B. in Gleichung einsetzt:
Das gegebene Lineare Gleichungssystem ist also eindeutig lösbar; für die Lösungsmenge erhält man .
gesucht; als Grundmenge wählt man die Menge der reellen Zahlen .
Jede der drei linearen Gleichungen lässt sich problemlos nach umstellen:
Setzt man jetzt die rechten Seiten der Gleichungen und gleich, so bedeutet dies - anschaulich gesprochen -, dass man die Schnittgerade der beiden durch diese Gleichungen beschriebenen Ebenen bestimmt:
Durch Einsetzen dieser Beziehung in Gleichung oder erhält man die zugehörigen -Koordinaten der Schnittgeraden; hier ergibt sich . Die folgende perspektivische Skizze zeigt diese Schnittgerade, Gleichung , als den Schnitt der durch die Gleichungen und beschriebenen, nicht parallelen Ebenen: Die vollkommen analoge Aussage gilt, falls man die rechten Seiten von Gleichung und gleichsetzt; man erhält dann die Schnittgerade der Ebenen und :
Deren -Koordinaten ergeben sich entsprechend durch Einsetzen dieser Beziehung in Gleichung oder zu . Eine diesem Sachverhalt entsprechende perspektivische Skizze aus derselben Blickrichtung zeigt diese Schnittgerade, Gleichung , als den Schnitt der durch die Gleichungen und beschriebenen, nicht parallelen Ebenen: Da im Ausgangssystem alle drei Gleichungen simultan gelten sollen, müssen auch die zwei gerade hergeleiteten Geradengleichungen gleichzeitig erfüllt sein. Im bildlichen Kontext suchen man daher den Schnittpunkt dieser beiden Geraden; diesen Schnittpunkt bekommt man, indem man die rechten Seiten der Gleichungen und gleichsetzt:
Den Lösungswert für kann man durch Einsetzen des Ergebnisses für z.B. in Gleichung berechnen:
Die folgende Skizze zeigt die Schnittgeraden, Gleichungen und , in der --Ebene, Projektion - Ansicht von oben -, und deren Schnittpunkt: Der Wert für schließlich resultiert, indem man die Werte für und z.B. in Gleichung einsetzt:
Das gegebene Lineare Gleichungssystem ist also eindeutig lösbar; für die Lösungsmenge erhält man .
- Liegen (mindestens) zwei der drei Ebenen parallel zueinander (ohne deckungsgleich zu sein), so besitzt das System keine Lösung: Parallele (nicht deckungsgleiche) Ebenen schneiden sich nicht; daher ist es unmöglich, die zu den Ebenen gehörenden Gleichungen simultan zu erfüllen.
- Sind zwei der drei Ebenen deckungsgleich, so wird die Schnittmenge mit der dritten (nicht parallelen und nicht deckungsgleichen) Ebene durch eine Schnittgerade gebildet; alle Punkte dieser Schnittgeraden repräsentieren Lösungen des Systems, die Lösungsmenge ist daher unendlich mächtig.
- Sind alle drei Ebenen deckungsgleich, so sind alle Punkte der (deckungsgleichen) Ebene(n) Lösungen des Systems; wiederum ist die Lösungsmenge unendlich mächtig.
- Eine eindeutige Lösung kann höchstens in diesem letzten Fall eintreten: Die drei (nicht parallelen und nicht deckungsgleichen) Ebenen führen auf drei Schnittgeraden (Ebene mit Ebene , Ebene mit Ebene , Ebene mit Ebene ):
- Liegen zwei Schnittgeraden parallel zueinander, so besitzt das System keine Lösung.
- Sind zwei Schnittgeraden deckungsgleich, so weist das System unendlich viele Lösungen auf.
- Schneiden sich die Schnittgeraden in einem Punkt, so ist die Lösung eindeutig und die Lösungsmenge besteht aus genau einem Element.
- Liegen zwei Schnittgeraden parallel zueinander, so besitzt das System keine Lösung.
Übrigens ist es im obigen Beispiel 4.3.3 nicht nötig, die dritte Schnittgerade zu bestimmen und zu überprüfen, dass diese dritte Schnittgerade die beiden anderen Geraden in deren Schnittpunkt schneidet: Dies ist automatisch gewährleistet, da durch das Gleichsetzen der rechten Seite von Gleichung mit derjenigen von Gleichung (erste Schnittgerade / Gleichung ) und durch das Gleichsetzen der rechten Seite von Gleichung mit derjenigen von Gleichung (zweite Schnittgerade / Gleichung ) die Gültigkeit der Gleichung für die dritte Schnittgerade (rechte Seite von = rechte Seite von ),
garantiert ist.
Im Beispiel wurde als rechnerisches Verfahren die Gleichsetzmethode verwendet, da sie sehr eng mit der anschaulich geometrischen Interpretation zusammenhängt. Durch das Gleichsetzen expliziter Ebenen- bzw. Geradengleichungen werden ja genau die Schnittgeraden bzw. -punkte bestimmt.
Info 4.3.4
Bei der Bei der Gleichsetzmethode werden die drei linearen Gleichungen in einem ersten Schritt nach einer der Unbekannten - oder nach einem Vielfachen einer der Unbekannten - umgestellt. Die resultierenden neuen Gleichungen werden dann im zweiten Schritt paarweise gleichgesetzt, wobei es genügt, dies für zwei Paare durchzuführen. Insgesamt entsteht ein Lineares Gleichungssystem, das nur noch aus zwei Gleichungen in (den verbliebenen) zwei Unbekannten aufgebaut ist und das anschließend mit den Methoden des Abschnitts 4.2 bearbeitet werden kann.
Aufgabe 4.3.5
Bestimmen Sie die Lösungsmenge des Linearen Gleichungssystems
Verwenden Sie die Gleichsetzmethode und gehen Sie geschickt vor!
Verwenden Sie die Gleichsetzmethode und gehen Sie geschickt vor!
 Onlinebrückenkurs Mathematik
Onlinebrückenkurs Mathematik