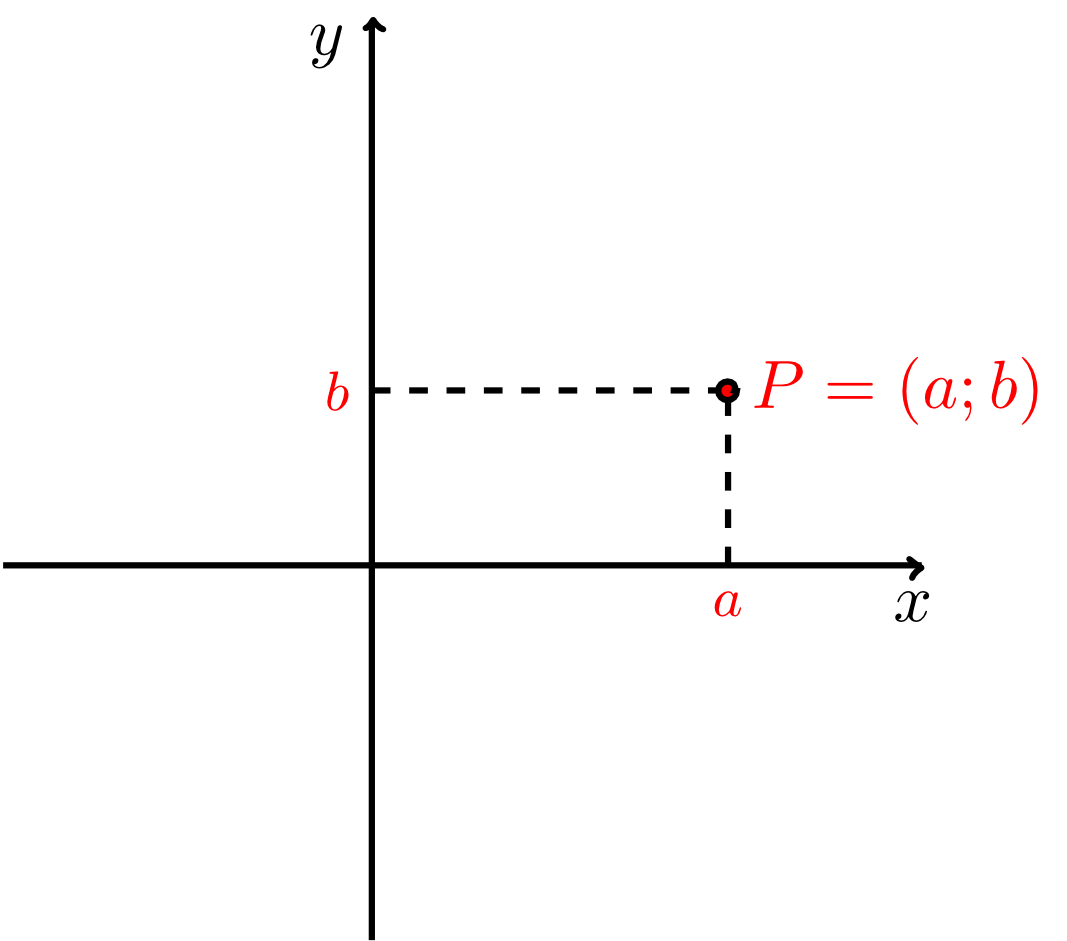Chapter 9 Objects in the Two-Dimensional Coordinate System
Section 9.1 Cartesian Coordinate System in the Plane9.1.2 Points in Cartesian Coordinate Systems
Now, if we want to describe points in the plane by coordinates, we use variables. Typically, points are denoted by upper-case Latin letters or , and their coordinates are denoted by lower-case Latin letters or . First, we will define what is meant by a point in the plane in which a coordinate system is given, and we will fix the notation that will be used in the rest of this course.
For points, there is some variation in notation. In schools, or is often written instead of . Throughout this course, the notation will be used. Since points are uniquely determined by their coordinates, we will not distinguish between a point and its coordinates in the following but we will consider both as the same object. For every coordinate system, the origin (the point with the coordinates ) is a special point. Generally, it is denoted by the variable : .
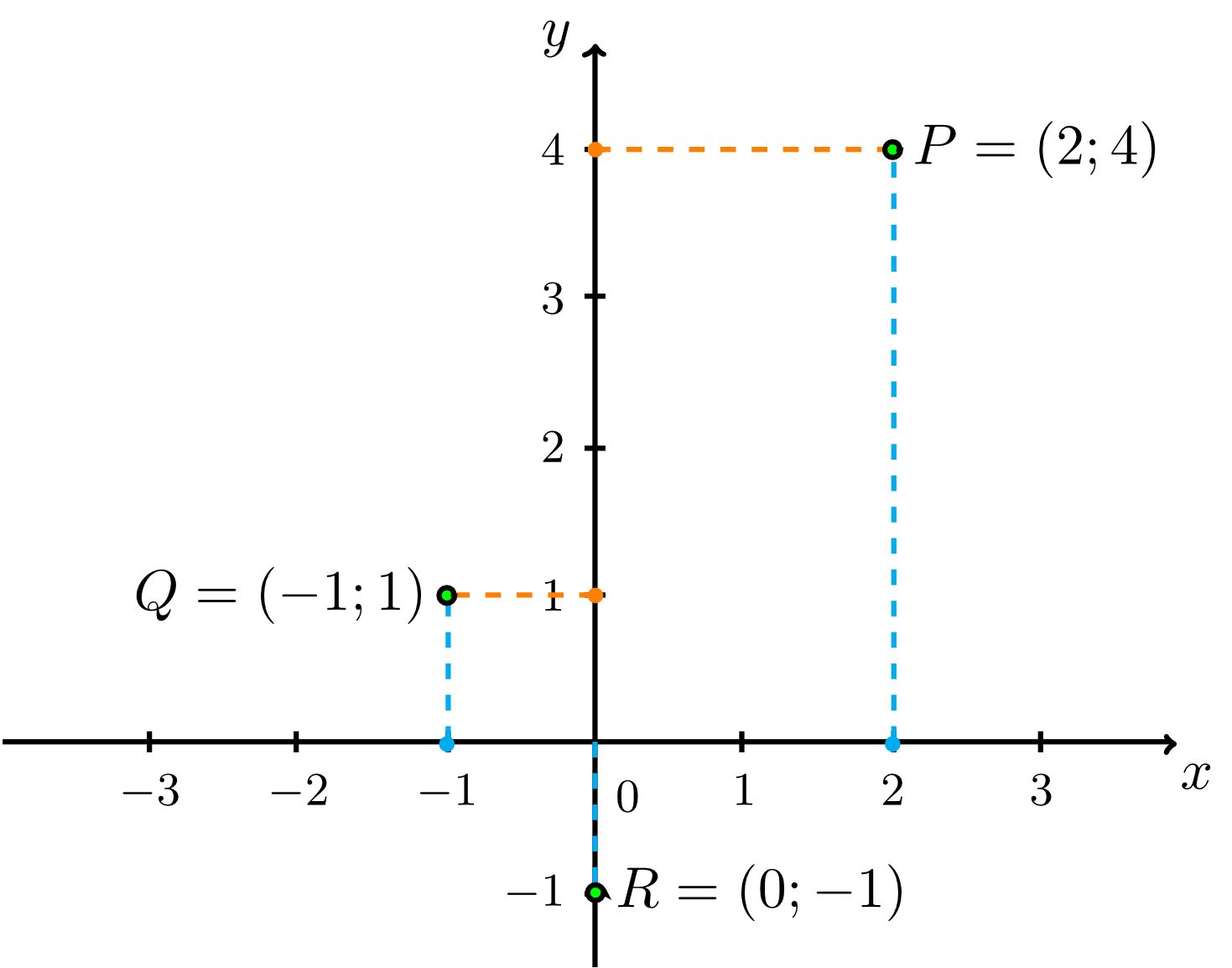
In the following sections we will describe further geometrical objects, such as lines and circles, by coordinates. For this purpose, we first have to understand that points in the plane (described by their coordinates with respect to a given coordinate system) can be collected into so-called sets of points. This is illustrated by the example below.
Exercise 9.1.5
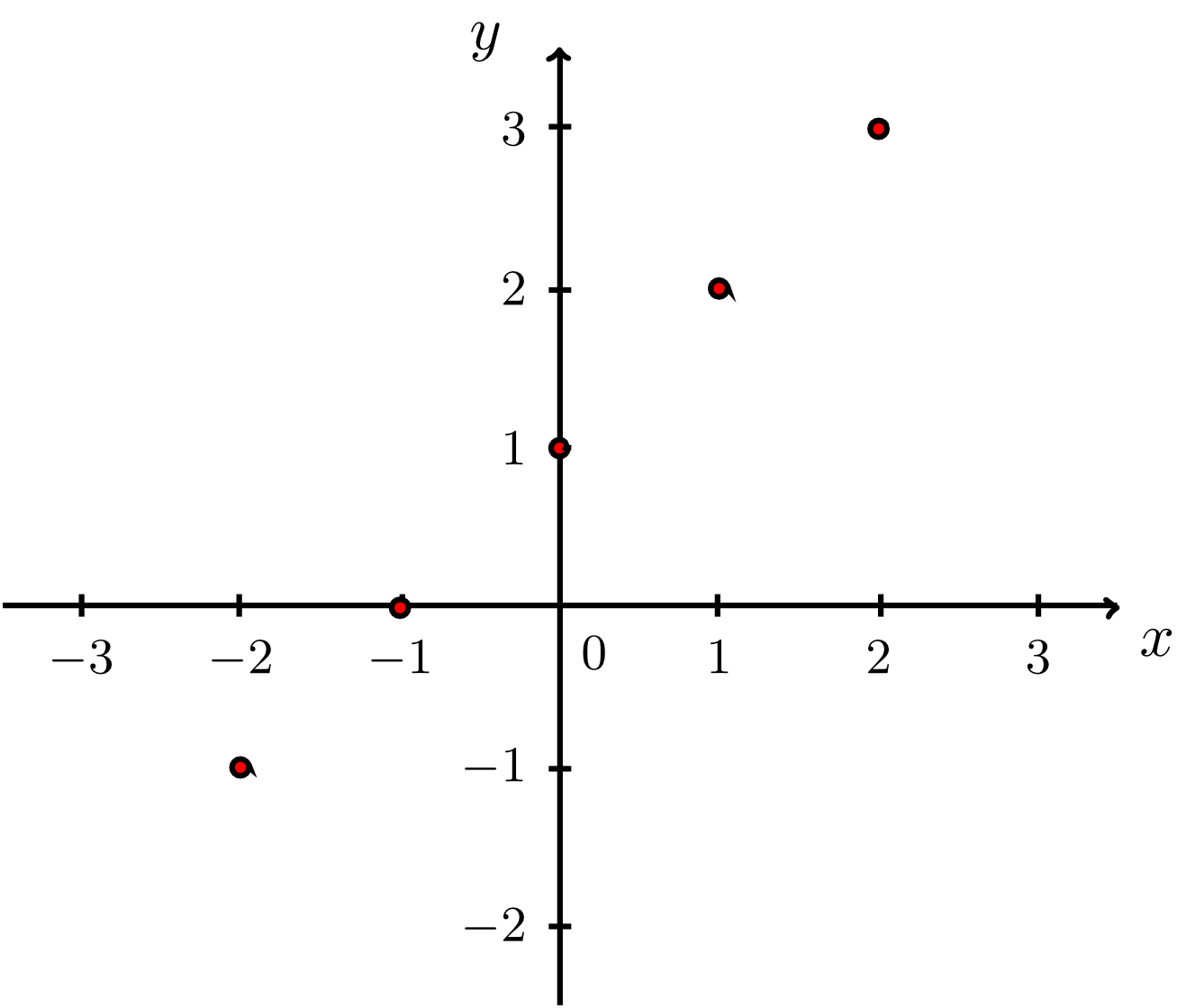
Draw the following sets of points in a Cartesian coordinate system.
-
-
- The set of all points in the first quadrant with integer abscissa smaller than and ordinate
As we know from Module 5, lines and circles are sets of an infinite number of points. It will be the subject of the following sections to describe their coordinates by means of sets of points and appropriate equations. A special infinite set of points is the collection of all points in a coordinate system in the plane. For this set, a specific notion exists.
Info 9.1.6
The set of all points in the plane described by the pairs of coordinates in a given Cartesian coordinate system is denoted by
The symbol reads as " two", " to the power of two", or " squared". This indicates that every point can be described by a pair of coordinates (also denoted as ordered pair) that consists of two real numbers.
 Onlinebrückenkurs Mathematik
Onlinebrückenkurs Mathematik