Chapter 7 Differential Calculus

Section 7.1 Derivative of a Function

7.1.2 Relative Rate of Change of a Function

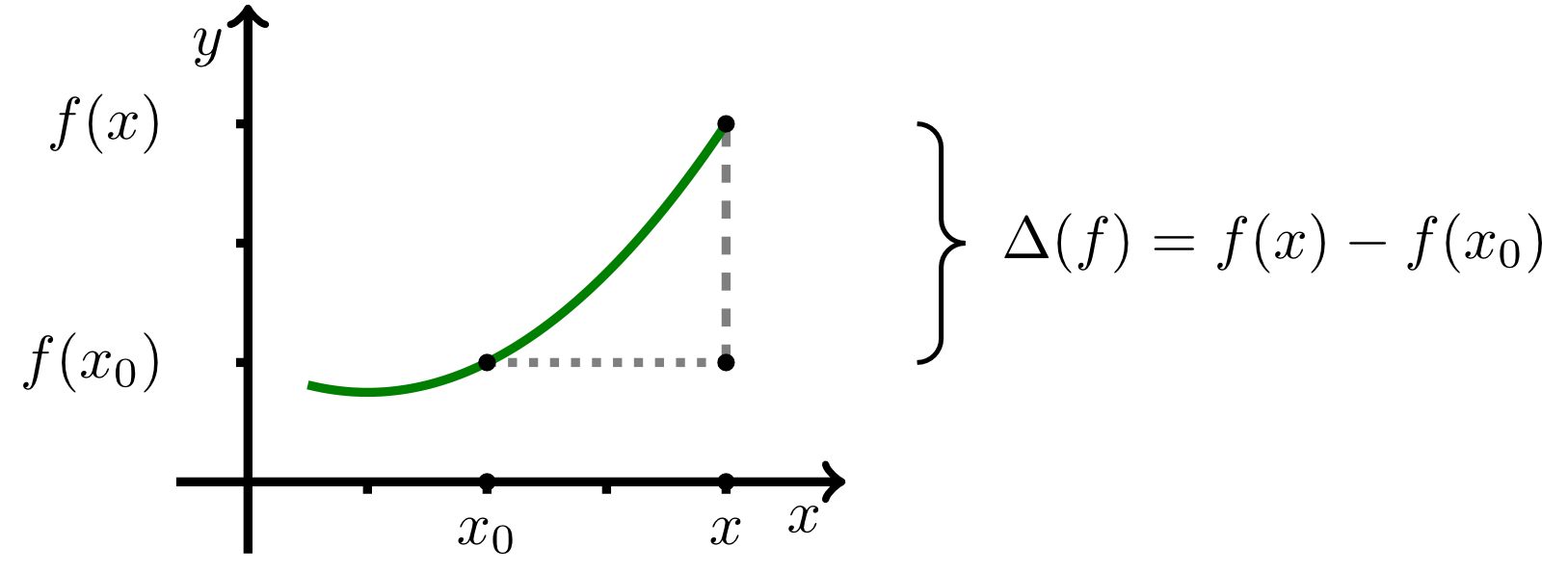
Consider a function $f:[a;b]\to ℝ$, $x\to f(x)$ and a sketch of the graph of $f$ (shown in the figure below). We would like to describe the rate of change of this function at an arbitrary point $x_0$ between $a$ and $b$. This will lead us to the notion of a derivative of a function. Generally, calculation rules are to be applied that are as simple as possible.

If $x_0$ and the corresponding function value $f\left(x_0\right)$ are fixed and another arbitrary, but variable point $x$ between $a$ and $b$ as well as the corresponding function value $f\left(x\right)$ are chosen, then through these two points, i.e. the points $(x_0;f(x_0))$ and $(x;f(x))$, a line can be drawn that is characterised by its slope and its $y$-intercept. For the slope of this line one obtains the so-called difference quotient

${\displaystyle \frac{\Delta (f)}{\Delta (x)}=\frac{f(x)-f(x_0)}{x-x_0}}$
that describes how the function values of $f$ between $x_0$ and $x$ change on average. Thus, an average rate of change of the function $f$ on the interval $[x_0;x]$ is found. This quotient is also called relative change.
If we let the variable point $x$ approach the point $x_0$, then we see that the line that intersects the graph of the function in the points $(x_0;f\left(x_0\right))$ and $(x;f\left(x\right))$ gradually becomes a tangent line to the graph in the point $(x_0;f\left(x_0\right))$. In this way, the rate of change of the function $f$ - or the slope of the graph of $f$ - at the point $x_0$ itself can be determined. If the approaching process of $x$ to $x_0$ described above leads to, figuratively speaking, a unique tangent line (i.e. a line with a unique slope that, in particular, must not be infinity), then in mathematical terms one says that the limit of the difference quotient does exist. This limiting process, i.e. letting $x$ approach $x_0$, is described here and in the following by the symbol

${\displaystyle \underset{x\to x_0}{lim}\hspace{0.5em},}$
where $lim$ is an abbreviation for the Latin word limes, meaning "border" or "boundary". If the limit of the difference quotient exists, then


${\displaystyle f\text{'}(x_0)=\underset{x\to x_0}{lim}\frac{\Delta (f)}{\Delta (x)}=\underset{x\to x_0}{lim}\frac{f(x)-f(x_0)}{x-x_0}}$
denotes the value of the derivative of $f$ at $x_0$. The function $f$ is then said to be differentiable at the point $x_0$.


Using the formula for the relative rate of change, calculating the derivative can be very cumbersome and also only works for very simple functions. Typically, the derivative is determined by applying calculation rules and inserting known derivatives for the individual terms.