Chapter 7 Differential Calculus
Section 7.4 Properties of Functions7.4.2 Monotony
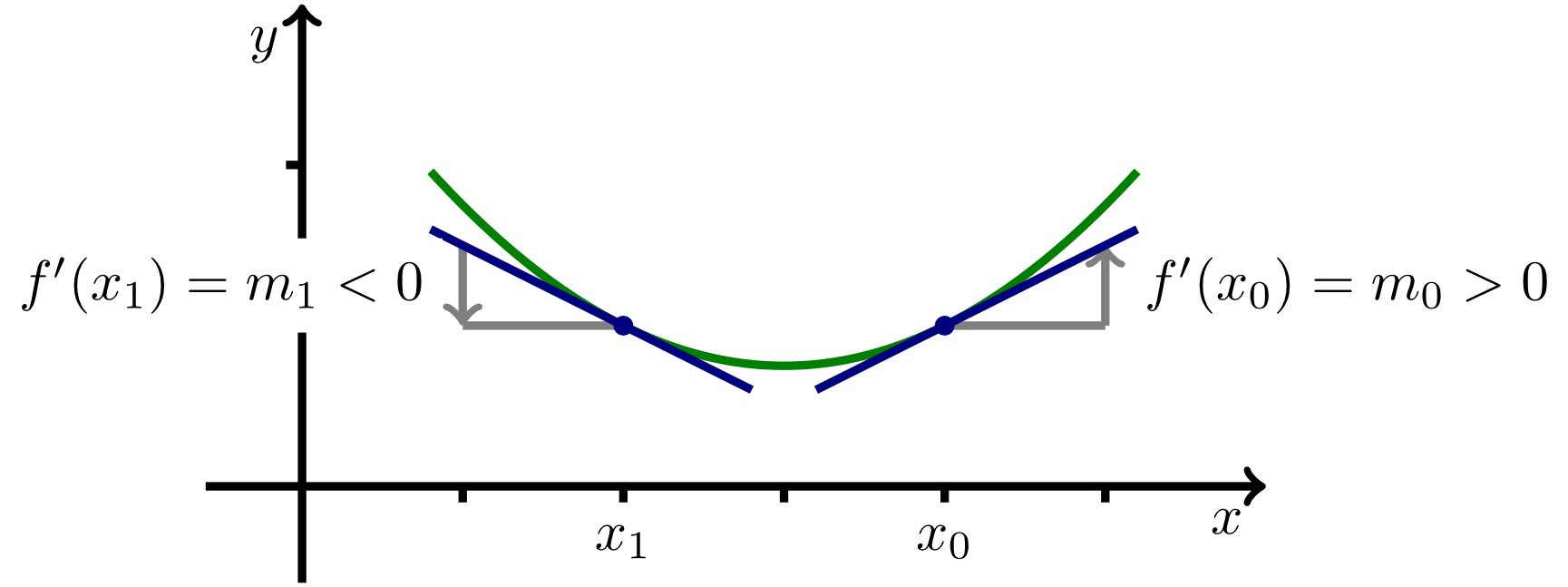
The derivative of a function can be used to study the growth behaviour, i.e. whether the function values increase or decrease for increasing values of . For this purpose, we consider a function that is differentiable on :
If for all between and , then is monotonically decreasing on the interval .
If for all between and , then is monotonically increasing on the interval .
Thus, it is sufficient to determine the sign of the derivative to decide whether a function is monotonically increasing or decreasing on the interval .
Example 7.4.1
The function is differentiable with . Since for all , we have , and therefore is monotonically increasing.
For with , the function has the roots and . If the monotony of the function is investigated, then three regions are to be distinguished in which has a different sign.
The following table is used to determine in which region the derivative of is positive or negative. These regions correspond to the monotony regions of . The entry "" says that the considered term is positive on the given interval. If the term is negative, then "" is entered.
For the function with , we have , that is for all .
Even though the function exhibits the same monotony behaviour for the two subregions and , it is not monotonically decreasing on the entire region. As a counterexample let us consider the function values and . Here, we have but also . This corresponds to an increasing growth behaviour if we change from one subregion to the other. The statement that the function is monotonically decreasing on thus means that the restriction of on this interval is monotonically decreasing. Moreover, the function is also monotonically decreasing for all .
For with , the function has the roots and . If the monotony of the function is investigated, then three regions are to be distinguished in which has a different sign.
The following table is used to determine in which region the derivative of is positive or negative. These regions correspond to the monotony regions of . The entry "" says that the considered term is positive on the given interval. If the term is negative, then "" is entered.
For the function with , we have , that is for all .
Even though the function exhibits the same monotony behaviour for the two subregions and , it is not monotonically decreasing on the entire region. As a counterexample let us consider the function values and . Here, we have but also . This corresponds to an increasing growth behaviour if we change from one subregion to the other. The statement that the function is monotonically decreasing on thus means that the restriction of on this interval is monotonically decreasing. Moreover, the function is also monotonically decreasing for all .
 Onlinebrückenkurs Mathematik
Onlinebrückenkurs Mathematik