Chapter 7 Differential Calculus
Section 7.4 Properties of Functions7.4.4 Exercises
Exercise 7.4.5
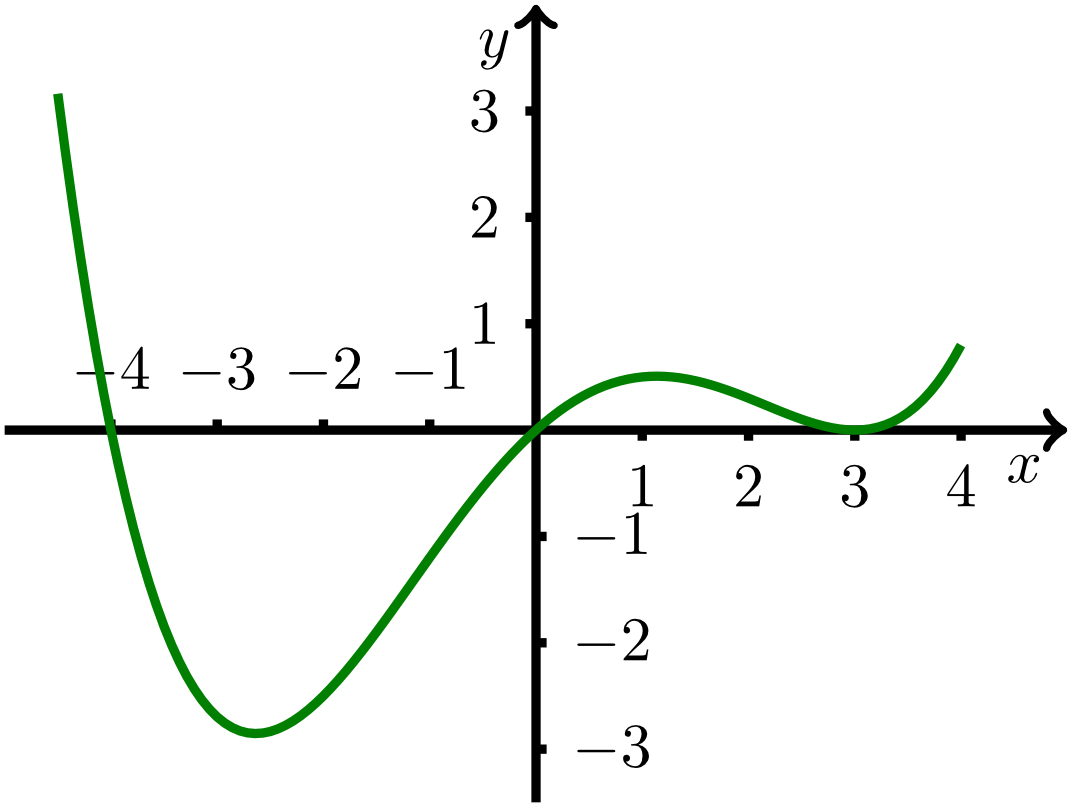
Specify the (maximum) open intervals on which the function with is monotonically increasing or decreasing.
Answer:
Answer:
- is monotonically
on .
- is monotonically
on .
Exercise 7.4.6
Specify the (maximum) open intervals on which the function with for is convex or concave. Answer:
- The function is convex on .
- The function is concave on .
Exercise 7.4.7
Consider the function with . Its derivative has the graph shown in the figure below:
Answer:
. The minimum point of is at .
- Where is the function monotonically increasing and where it is monotonically decreasing? Find the maximum open intervals on which has this property.
- What can you say about the maximum and minimum points of the function ?
Answer:
- The function is monotonically
on
.
- The function is monotonically
on
.
- The function is monotonically
on .
- The function is monotonically
on .
. The minimum point of is at .
 Onlinebrückenkurs Mathematik
Onlinebrückenkurs Mathematik