Chapter 7 Differential Calculus

Section 7.1 Derivative of a Function

7.1.3 Derivative

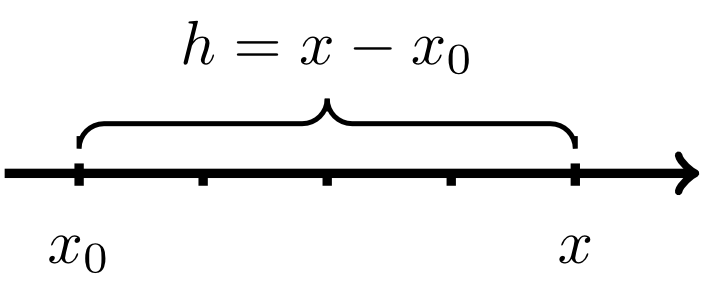
If the derivative is to be calculated using the difference quotient $\frac{f(x)-f(x_0)}{x-x_0}$, then it is often convenient to rewrite the difference quotient in another way. Denoting the difference of $x$ and $x_0$ by $h:=x-x_0$ (see figure below),

the difference quotient can be rewritten as

${\displaystyle \frac{f(x)-f(x_0)}{x-x_0}=\frac{f(x_0+h)-f(x_0)}{h}\hspace{0.5em},}$
where $x=x_0+h$. There is no statement about whether $x$ has to be greater or less than $x_0$. Hence, the quantity $h$ can take positive or negative values. To determine the derivative of the function $f$, the limit for $h\to 0$ has to be calculated:

${\displaystyle f\text{'}(x_0)=\underset{x\to x_0}{lim}\frac{f(x)-f(x_0)}{x-x_0}=\underset{h\to 0}{lim}\frac{f(x_0+h)-f(x_0)}{h}\hspace{0.5em}.}$
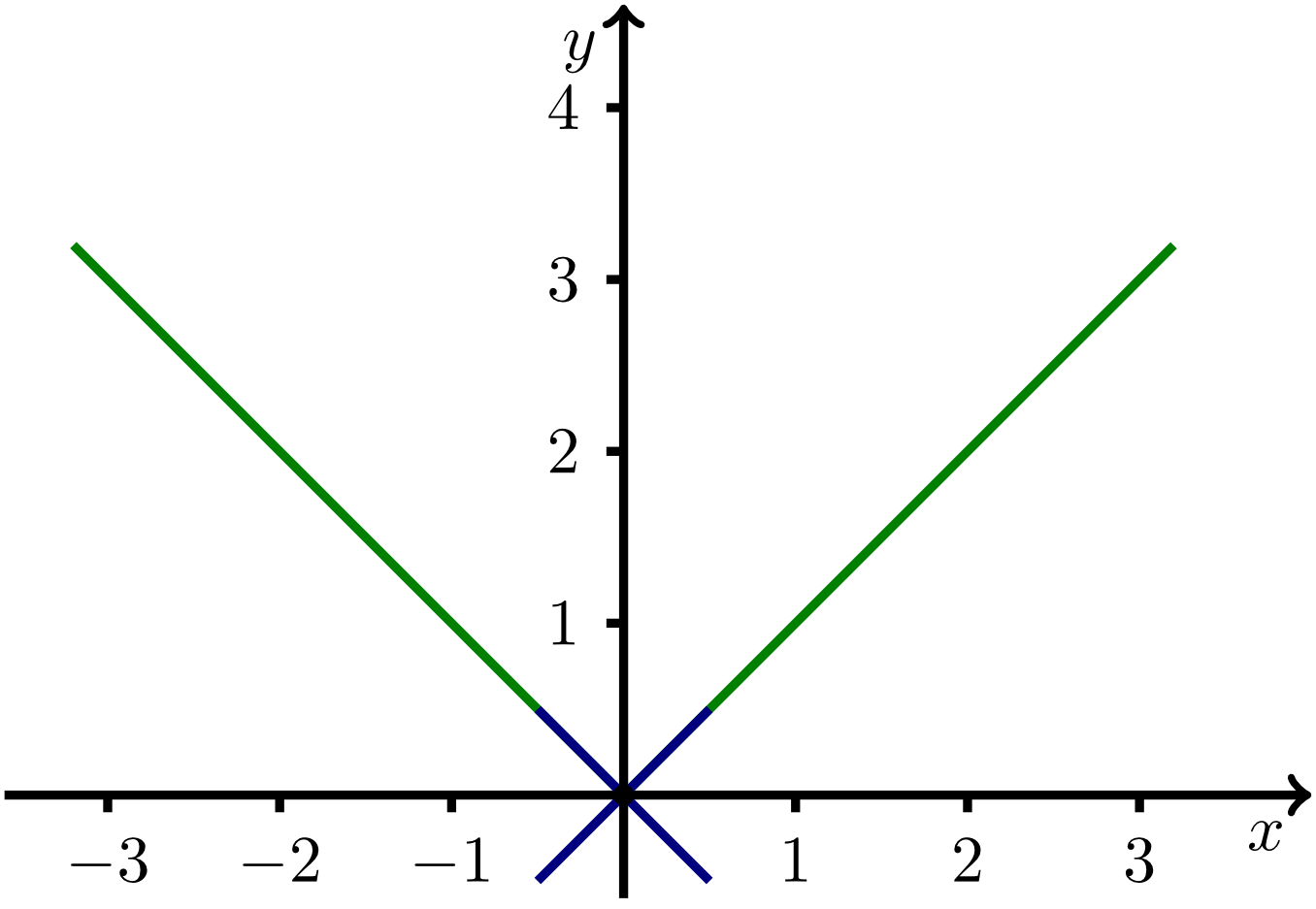
If this limit exists for all points $x_0$ in a function's domain, then the function is said to be differentiable (everywhere). Many of the common functions are differentiable. However, a simple example of a function that is not differentiable everywhere is the absolute value function $f:ℝ\to ℝ$ with $x\to f(x):=|x|$.

Likewise, if a function has a jump at a certain point, a unique tangent line to the graph at this point does not exist and thus, the function has no derivative at this point.