Chapter 7 Differential Calculus
Section 7.2 Standard Derivatives7.2.2 Derivatives of Power Functions
In the last section, the derivative was introduced as the limit of the difference quotient. Accordingly, for a linear affine function (see Module 6, Section 6.2.4) , , where and are given numbers, we obtain for the derivative at the point the value . (Readers are invited to verify that fact themselves.)
For monomials with , it is easiest to determine the derivative using the difference quotient. Without any detailed calculation or any proof we state the following rules:
Derivative of 7.2.1
Let a natural number and a real number be given.
The constant function with has the derivative with .
The function with has the derivative
This differentiation rule is true for all .
The constant function with has the derivative with .
The function with has the derivative
This differentiation rule is true for all .
Again, we leave the verification of these statements to the reader.
Example 7.2.2
Let us consider the function with . According to the notation above, this is a function with and . Thus for the value of the derivative at the point , we have
For root functions, an equivalent statement holds. However, it should be noted that root functions are only differentiable for since the tangent line to the graph of the function at the point is parallel to the -axis and thus, it is not a graph of a function.
Derivative of 7.2.3
For with , the function , is differentiable for , and we have
For , root functions are described by . Of course, the differentiation rule given here also holds for or .
Example 7.2.4
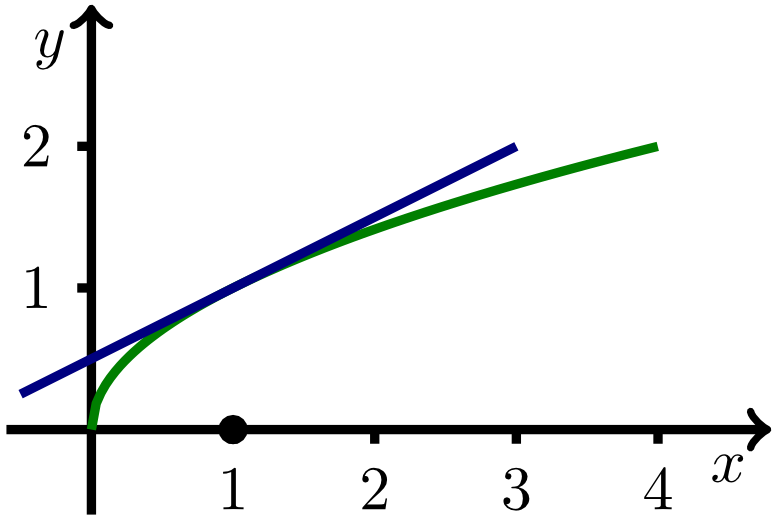
The root function with is differentiable for . The value of the derivative at an arbitrary point is given by
The derivative at the point does not exist since the slope of the tangent line to the graph of would be infinite there.
The tangent line to the graph of the given root function at the point has the slope .
The derivative at the point does not exist since the slope of the tangent line to the graph of would be infinite there.
The tangent line to the graph of the given root function at the point has the slope .
For , the statements above can be extended to exponents with : The value of the derivative of the function with the mapping rule is, for ,
 Onlinebrückenkurs Mathematik
Onlinebrückenkurs Mathematik