Chapter 7 Differential Calculus

Section 7.2 Standard Derivatives

7.2.3 Derivatives of Special Functions

Derivatives of Trigonometric Functions

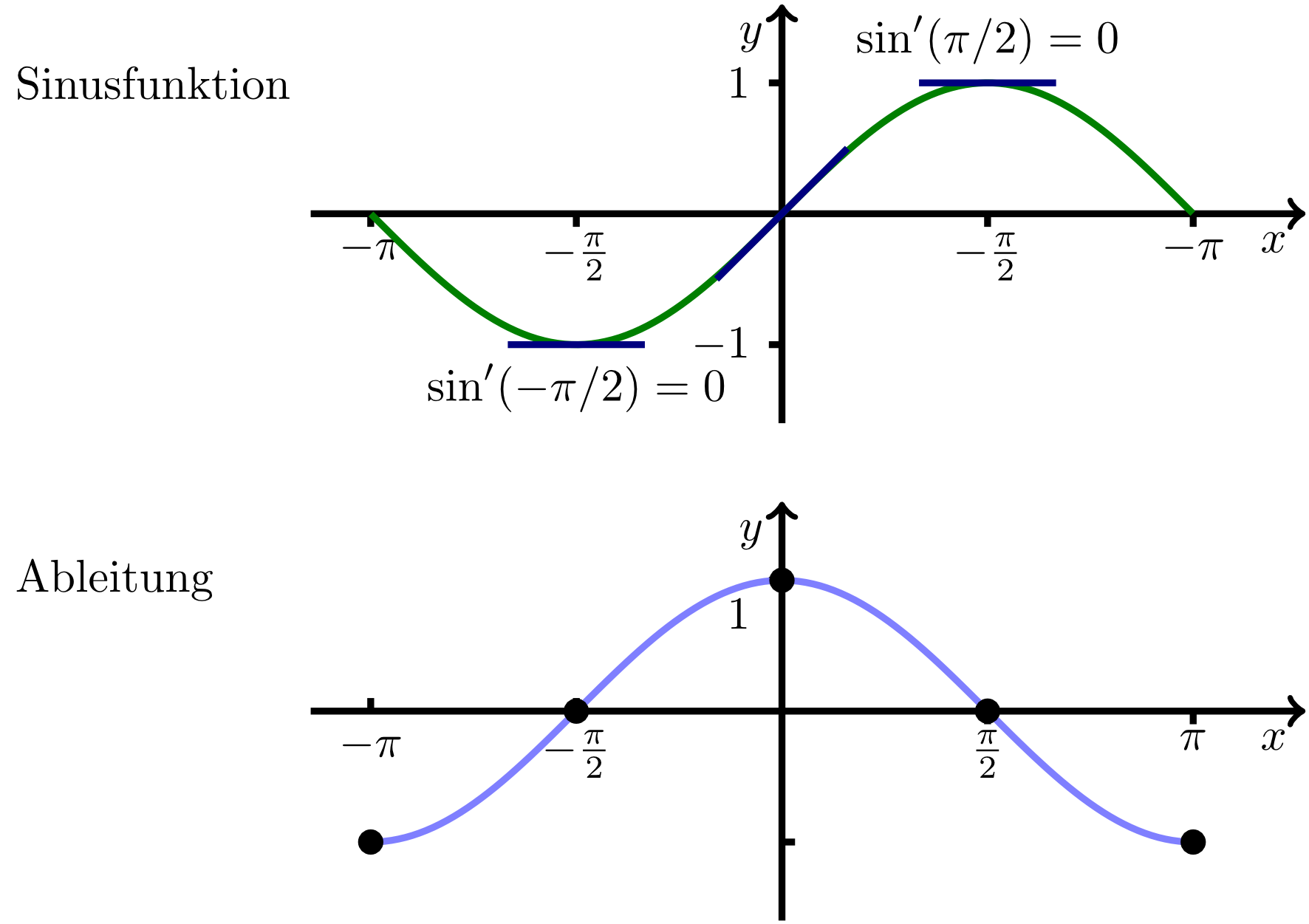
The sine function $f:ℝ\to ℝ$, $x\to f(x)=\sin (x)$ is periodic with period $2\pi$. Thus, it is sufficient to consider the function on an interval of length $2\pi$. A section of the graph for $-\pi \le x\le \pi$ is shown in the figure below:

As we see from the figure above, the slope of the sine function at $x_0=\pm \frac{\pi }{2}$ is $f\text{'}(\pm \frac{\pi }{2})=0$. The tangent line to the graph of the sine function at $x_0=0$ has the slope $f\text{'}(0)=1$. At $x_0=\pm \pi$, the tangent line has the same slope as the tangent line at $x_0=0$, but the sign is opposite. Hence, the slope at $x_0=\pm \pi$ is $f\text{'}(\pm \pi )=-1$. Thus, the derivative of the sine function is a function that exhibits exactly these properties. A detailed investigation of the regions between these specially chosen points shows that the derivative of the sine function is the cosine function:

This last result comes from the calculation rules explained (explained below) and the definition of the tangent function as the quotient of the sine function and the cosine function.

Derivative of the Exponential Function

Derivative of the Logarithmic Function

The derivative of the logarithmic function is given here without proof. For $f:]0;\infty [\to ℝ$ with $x\to f(x)=\ln (x)$ one obtains $f\text{'}:]0;\infty [\to ℝ$, $x\to f\text{'}(x)=\frac{1}{x}$.