Chapter 6 Elementary Functions
Section 6.2 Linear Functions and Polynomials6.2.5 Absolute Value Functions
In Module 2 the absolute value of a real number was introduced in the following way:In the context of this module, the absolute value can be regarded as a function. This results in the absolute value function:
Exercise 6.2.6
What is the range of the absolute value function ?
Due to the definition by cases
the absolute value function is an example of a piecewise defined function. If absolute values are defined according to different cases, then it is also said that the absolute value is resolved. Then, the graph of the absolute value function looks as follows:
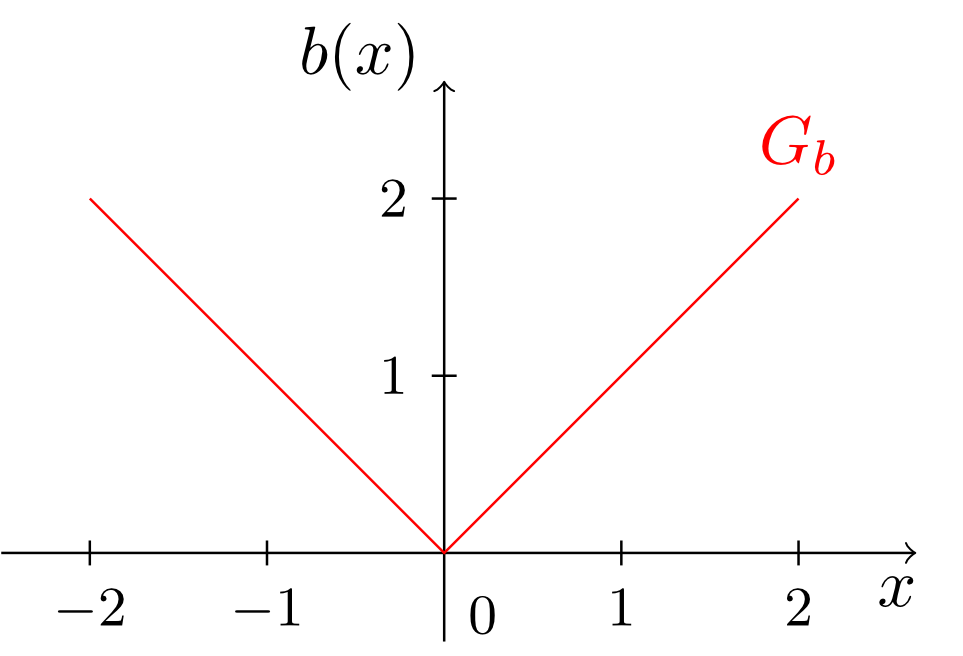
One property of the graph of the absolute value function, which most of the more general functions involving absolute values have in common, is the kink at . The absolute value function defined above is only the simplest case of a function involving an absolute value. More complicated examples of functions can be constructed, involving one or several absolute values, e.g.
For such functions, it is a relevant task to get an idea of how the graph of the function looks. To do this, we use the piecewise definition of the absolute value, and the approach is similar to the one for the solution of absolute value equations and inequalities. Here, we demonstrate this approach for the example of the function defined above:
Example 6.2.7
Consider the function
What does the graph look like?
We calculate:
Thus, we obtain a piecewise defined function whose graph is an increasing line with the slope and the -intercept for in the region and a decreasing line with the slope and the -intercept for in the region . With this information we can draw the graph of :
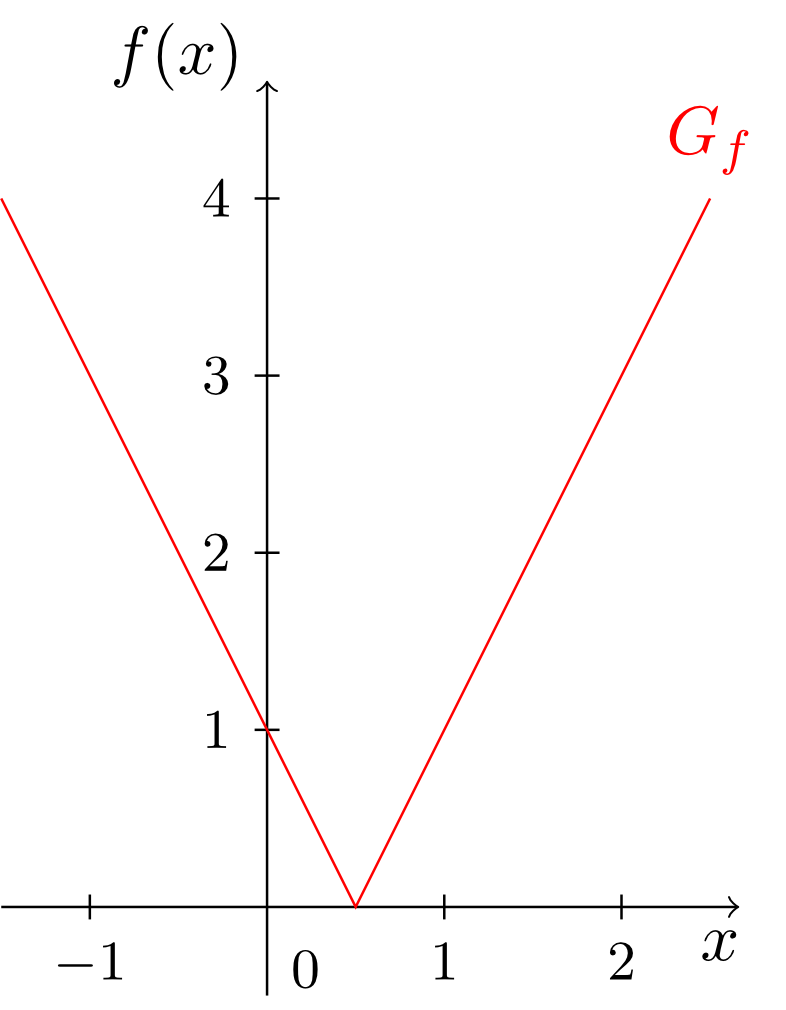
What does the graph look like?
We calculate:
Thus, we obtain a piecewise defined function whose graph is an increasing line with the slope and the -intercept for in the region and a decreasing line with the slope and the -intercept for in the region . With this information we can draw the graph of :

Info 6.2.8
CAUTION! If absolute values are resolved as in the calculation in the example above, two important calculation rules have to be observed:
- The regions for the cases are defined by inequalities for the entire expression between the absolute value bars, here and , and not only by and . It is always that way if absolute values are resolved.
- For the case the entire expression gets a minus sign. Here, care has to be taken that the expression is bracketed. In the example above, we therefore have and not . This is always the case if absolute values are resolved.
Exercise 6.2.9
Sketch the graph of the function
Moreover, specify its range .
Moreover, specify its range .
 Onlinebrückenkurs Mathematik
Onlinebrückenkurs Mathematik
