Chapter 6 Elementary Functions

Section 6.2 Linear Functions and Polynomials

6.2.4 Linear Affine Functions

Combining linear functions with constant functions results in so-called linear affine functions. These are the sum of a linear function and a constant function. Generally, without any specification for the slope ($m\in ℝ$) this is written as follows:

${\displaystyle f:\mathrm{\hspace{0.5em}\hspace{0.5em}}\{\begin{array}{ccc}\hfill ℝ& \hfill \to \hfill & ℝ\hfill \\ \hfill x& \hfill ⟼\hfill & mx+c\hspace{0.5em}.\hfill \end{array}}$


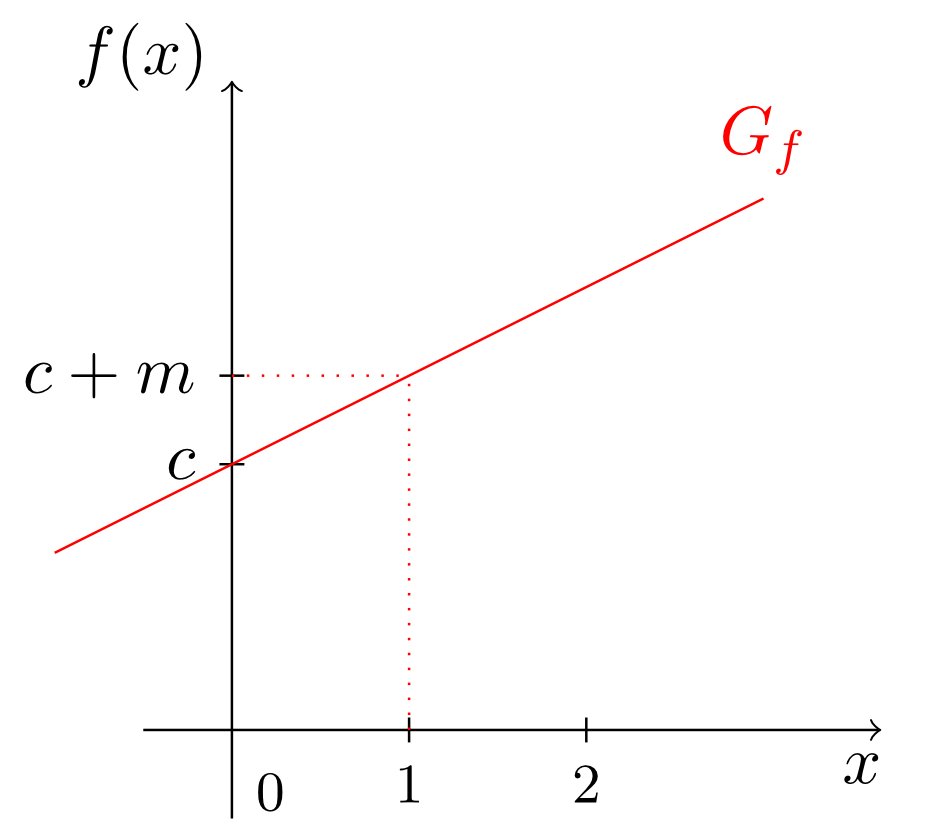
The graphs of linear affine functions are also called lines. For linear affine functions, the constant $m$ is still called slope, and the constant $c\in ℝ$ is called $y$-intercept. The reason for this term is as follows: if the intersection point of the graph of the linear affine function with the vertical axis is considered, then this point has the distance $c$ from the origin (see figure above). So, for the linear affine function shown in the figure below

${\displaystyle f:\mathrm{\hspace{0.5em}\hspace{0.5em}}\{\begin{array}{ccc}\hfill ℝ& \hfill \to \hfill & ℝ\hfill \\ \hfill x& \hfill ⟼\hfill & -2x-1\hfill \end{array}}$


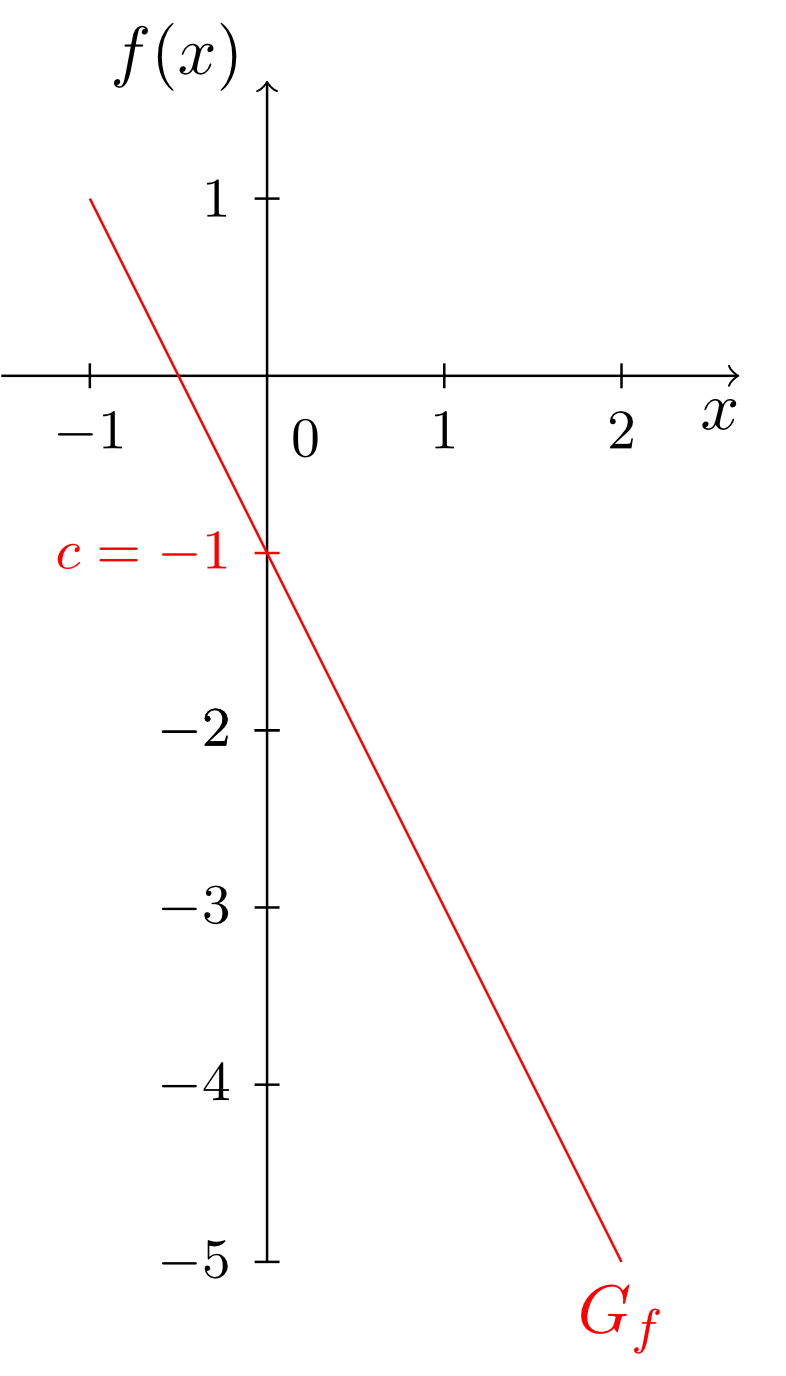
we have the slope $m=-2$ and the $y$-intercept $c=-1$. The $y$-intercept is the value of the function at $x=0$ and hence given by

${\displaystyle c=f(0)=-2·0-1=-1\hspace{0.5em}.}$