Kapitel 7 Differentialrechnung
Abschnitt 7.2 Standardableitungen7.2.2 Ableitung von Potenzfunktionen
Aus der Einführung der Ableitung als Grenzwert des Differenzenquotienten ergibt sich für eine affin lineare Funktion (siehe Modul 6, Abschnitt (VERWEIS)) , , wobei und gegebene Zahlen sind, dass der Wert der Ableitung von an der Stelle gleich ist. (Die geneigte Leserin, der geneigte Leser möge dies gerne selbst überprüfen!)
Für Monome mit ist es am einfachsten, die Ableitung über den Differenzenquotienten zu bestimmen. Ohne hier eine detaillierte Rechnung oder einen Beweis anzugeben, erhält man die folgenden Aussagen:
Ableitung von 7.2.1
Gegeben sind eine natürliche Zahl und eine reelle Zahl .
Die konstante Funktion mit besitzt die Ableitung
Die Funktion mit besitzt die Ableitung
Diese Ableitungsregel gilt im Übrigen auch für .
Die konstante Funktion mit besitzt die Ableitung
Die Funktion mit besitzt die Ableitung
Diese Ableitungsregel gilt im Übrigen auch für .
Auch die Überprüfung dieser Aussagen sei dem Selbststudium überlassen!
Beispiel 7.2.2
Die folgende Untersuchung gilt der Funktion mit . Der Vergleich der gegebenen Funktion mit den oben verwendeten Bezeichnungen ergibt und . Damit erhält man für den Wert der Ableitung an der Stelle
Für Wurzelfunktionen ergibt sich eine entsprechende Aussage. Allerdings ist zu beachten, dass Wurzelfunktionen nur für differenzierbar sind. Denn die Tangente an den Funktionsgraphen durch den Punkt verläuft parallel zur -Achse und ist somit kein Schaubild einer Funktion.
Ableitung von 7.2.3
Für mit ist die Funktion , für differenzierbar, und es gilt
Für werden durch Wurzelfunktionen beschrieben. Die hier wiedergegebene Ableitungsregel gilt natürlich auch für oder , da sie für ganze Zahlen gültig ist.
Beispiel 7.2.4
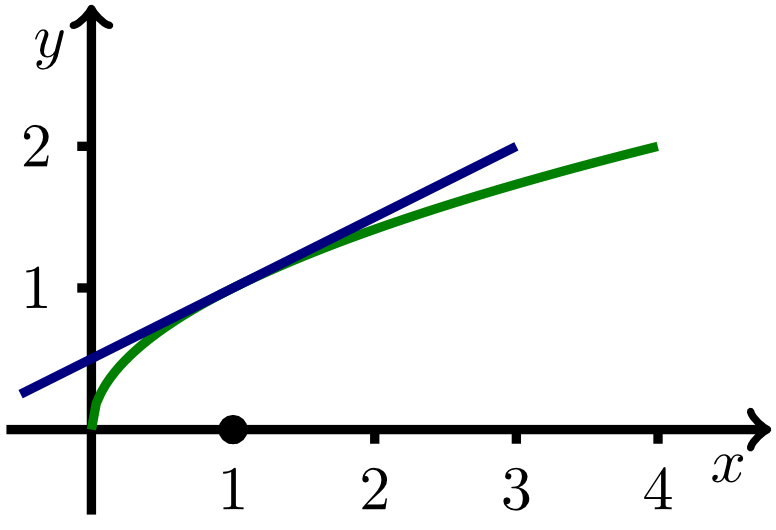
Die Wurzelfunktion mit ist für differenzierbar. Der Wert der Ableitung an einer beliebigen Stelle ist durch
gegeben. Die Ableitung in existiert nicht, da die Tangente an den Graphen von dort eine unendliche Steigung hätte.
Die Tangente im Punkt an den Graphen der vorliegenden Wurzelfunktion weist die Steigung auf.
gegeben. Die Ableitung in existiert nicht, da die Tangente an den Graphen von dort eine unendliche Steigung hätte.
Die Tangente im Punkt an den Graphen der vorliegenden Wurzelfunktion weist die Steigung auf.
Die bisherigen Aussagen können für auf Exponenten mit ausgedehnt werden: Der Wert der Ableitung einer Funktion mit Funktionsterm für ist
 Onlinebrückenkurs Mathematik
Onlinebrückenkurs Mathematik