Chapter 9 Objects in the Two-Dimensional Coordinate System

Section 9.2 Lines in the Plane

9.2.3 Relative Positions of Lines


In the previous Section 9.2.2 we discussed how to describe lines by means of equations in coordinate form and how to find the equations of a line from given data. This section investigates the relative positions of lines (given by equations) with respect to each other and with respect to other given points. The latter question can be answered very easily since a point either lies on a line or it does not.
Info 9.2.12
 
Let a line

g={(x;y) : px+qy=c}

and a point P=(a;b) in ℝ2 be given. The point P lies on the line (i.e. P∈g) if and only if its abscissa and its ordinate satisfy the equation of the line, i.e. if we have

pa+qb=c .


Thus, using an equation of the line, we can check whether points lie on the line or do not.
Example 9.2.13
Let us consider the line

h: x+2y=-1 .

We see that the point A= (-2; 1 2 ) lies on h since its coordinates x=-2 and y= 1 2 satisfy the equation of a line, i.e.

-2+2· 1 2 =-2+1=-1 .

The point B=(1;1), however, does not lie on h since its coordinates x=1 and y=1 do not satisfy the equation of a line, i.e.

1+2·1=3≠-1 .

This is illustrated by the figure below.

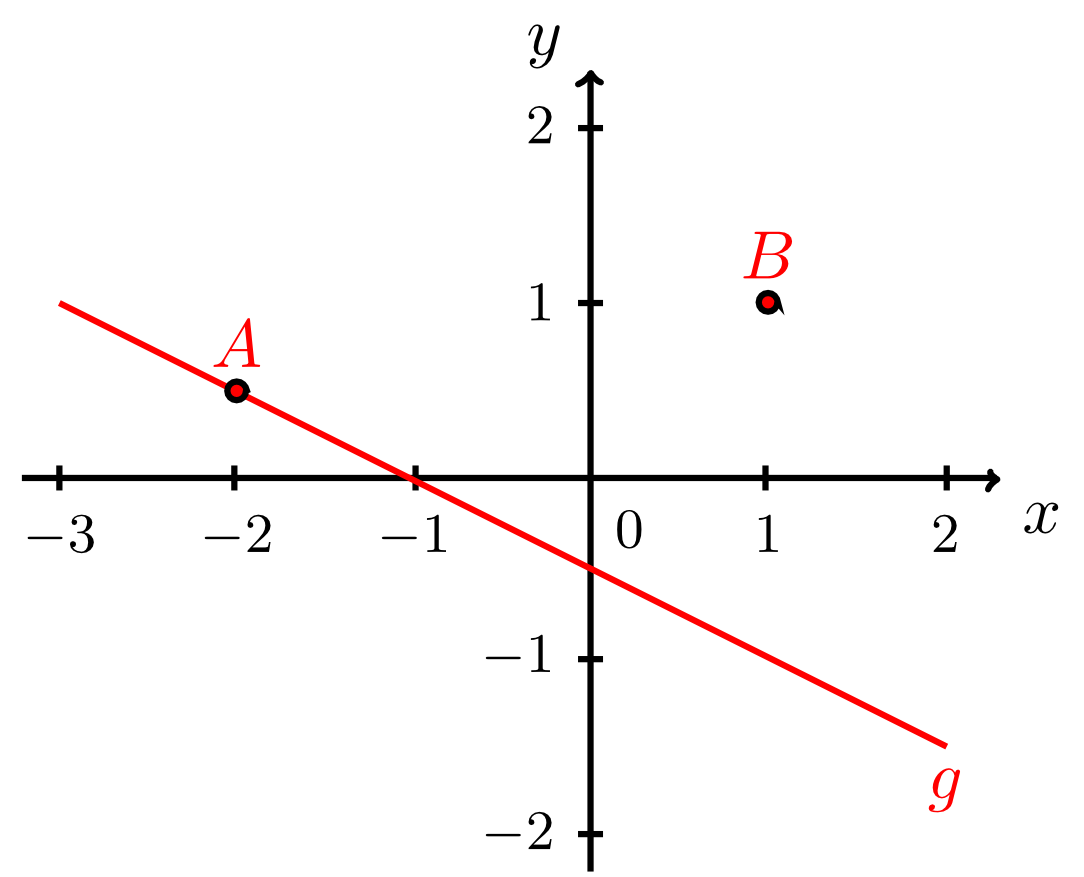
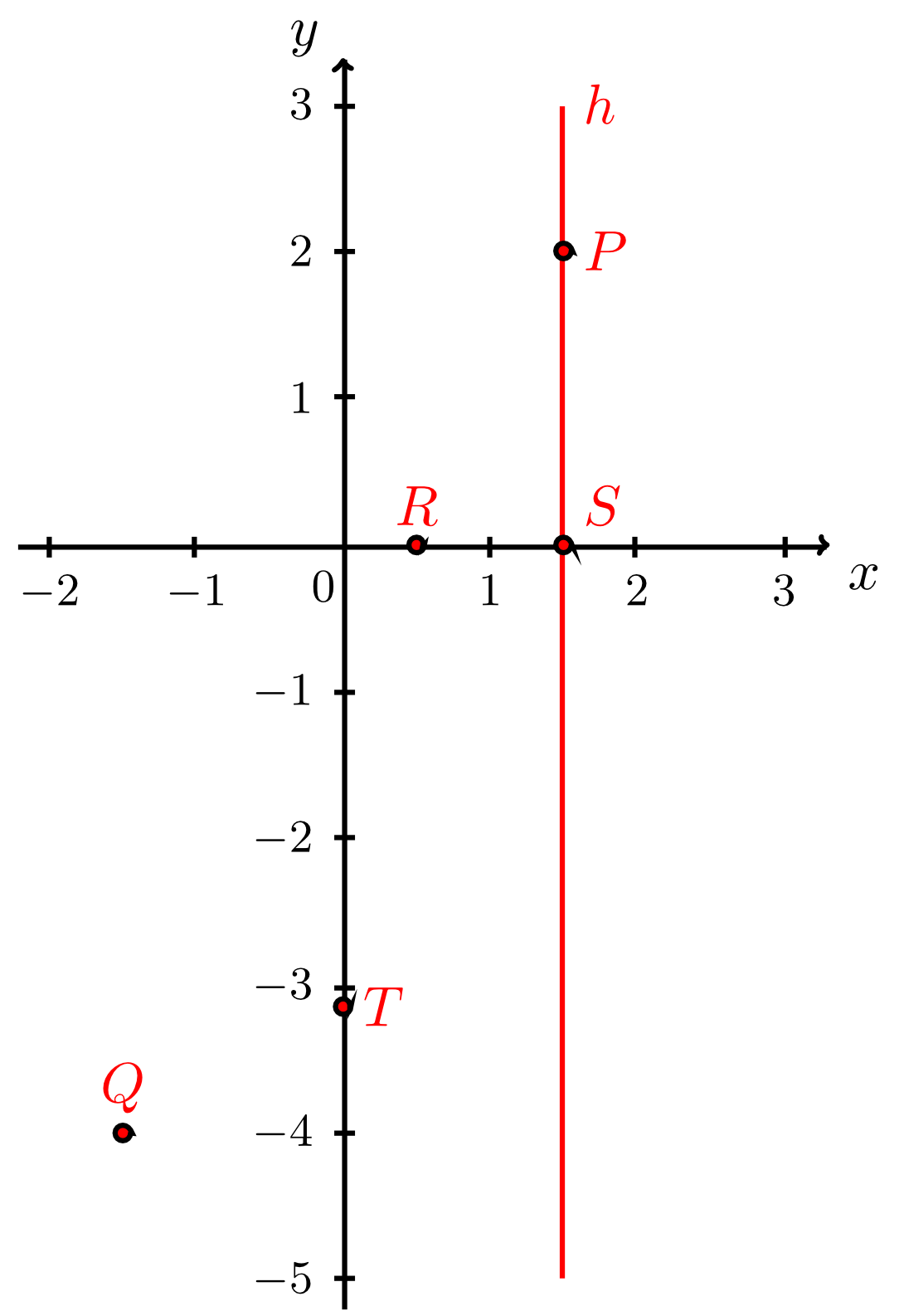
Exercise 9.2.14
Decide whether the given points lie on the given lines by inserting and calculating. Tick the points that lie on the line.

g: 2x-4( y 2 +x)+2y=-3:

   P=(1.5;2)
   Q= (- 3 2 ;-4 )
   R=(0.5;0)
   S= ( 9 6 ;0 )
   T=(0;-π)




Two lines on a plane can have three different relative positions:
Info 9.2.15
 
Let g and h be two lines in the plane that are described by equations of a line with respect to a coordinate system. Then the lines have exactly one of the following relative positions with respect to each other:
  1. The lines g and h have exactly one point in common, i.e. they intersect. The common point is called the intersection point.
  2. The lines g and h do not have any points in common, i.e. they do not intersect at all. In this case, the lines are parallel.
  3. The lines g and h have all their point in common, i.e. they are identical. In this case, the lines are coincident.

The last case seems to be a little strange at first glance. You may wonder why two names ( g and h) exist for the same object. Different equations can in fact describe exactly one and the same line if the equations arise from each other by equivalent transformations. Sometimes this is not obvious but can be seen from a detailed investigation. This idea is illustrated by the example below.
Example 9.2.16
  1. The lines g: y=2x-1 and h: y=x+1 intersect. The only point they have in common is the intersection point S=(2;3):
  2. The lines g: y= 1 2 x-1 and h: x-2y=-2 do not intersect. They are parallel to each other:
  3. The lines g: y= 1 3 x+1 and h: 2x-6y=-6 are coincident since they arise from each other by equivalent transformations:

    y= 1 3 x+1  ⇔  y- 1 3 x=1  |·(-6)  ⇔  2x-6y=-6




The methods for calculating the intersection point of lines are the methods for solving a system of two linear equations in two variables (in this case these are the equations of a line) that were discussed in detail in Module 4. In particular, the geometrical aspect of the intersection point of lines was discussed in detail in Section 4.2 in this context. Hence, for the methods of finding an intersection point, we refer to Section 4.2 and highly recommend a brief repetition of the material presented there.
However, if two equations of a line are given in normal form, i.e. if their slopes and y-intercepts are known, then it can be seen immediately (without a calculation) which of the three relative positions defined in Info Box 9.2.15 applies to the two lines:
Info 9.2.17
 
Let two lines g and h in the plane be given by equations in normal form.
  1. If the slopes of g and h are different, the two lines intersect.
  2. If the slopes of g and h are the same, but their y-intercepts are different, the two lines are parallel.
  3. If the slopes and y-intercepts of g and h are the same, the two lines are coincident.


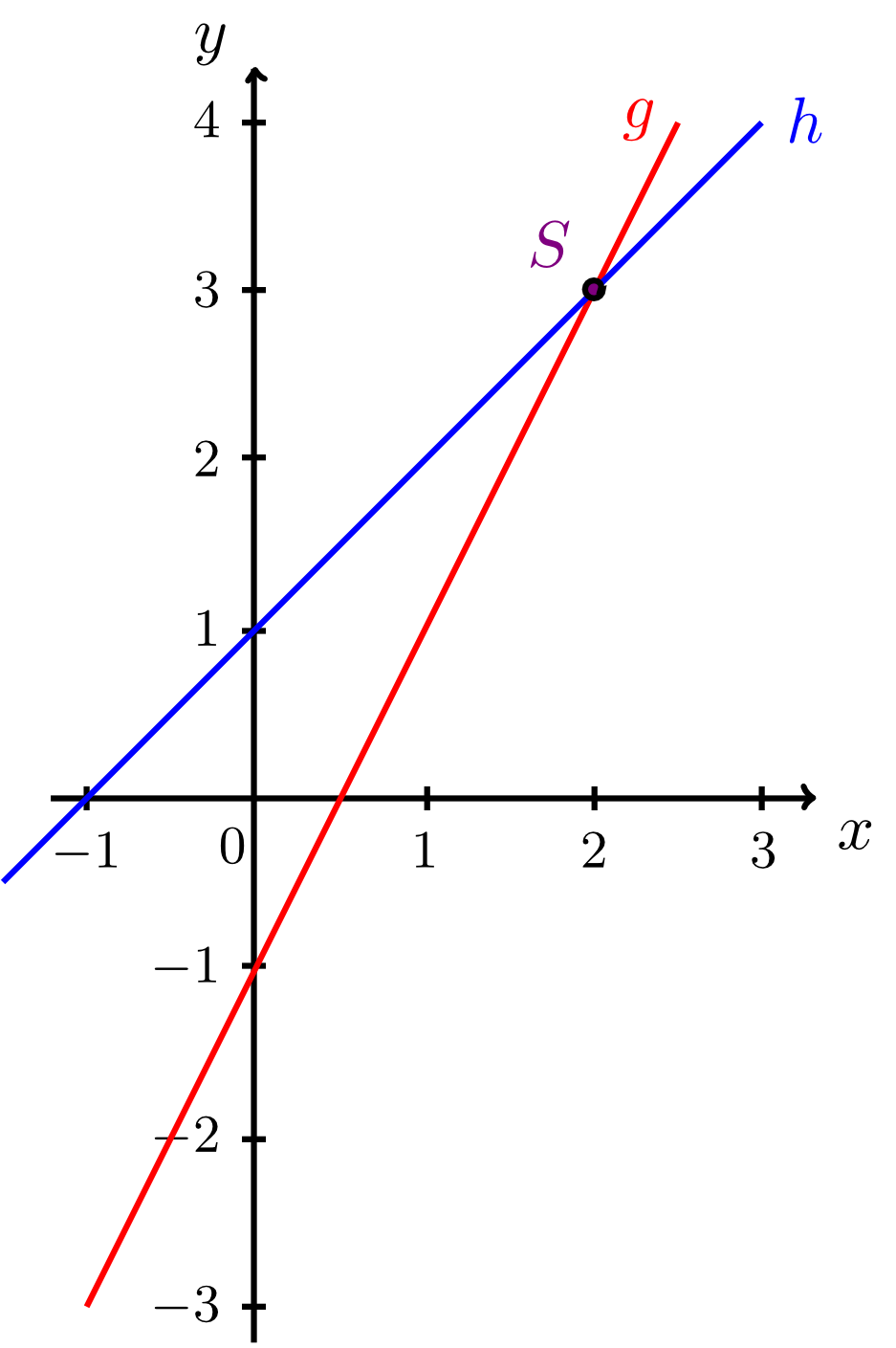
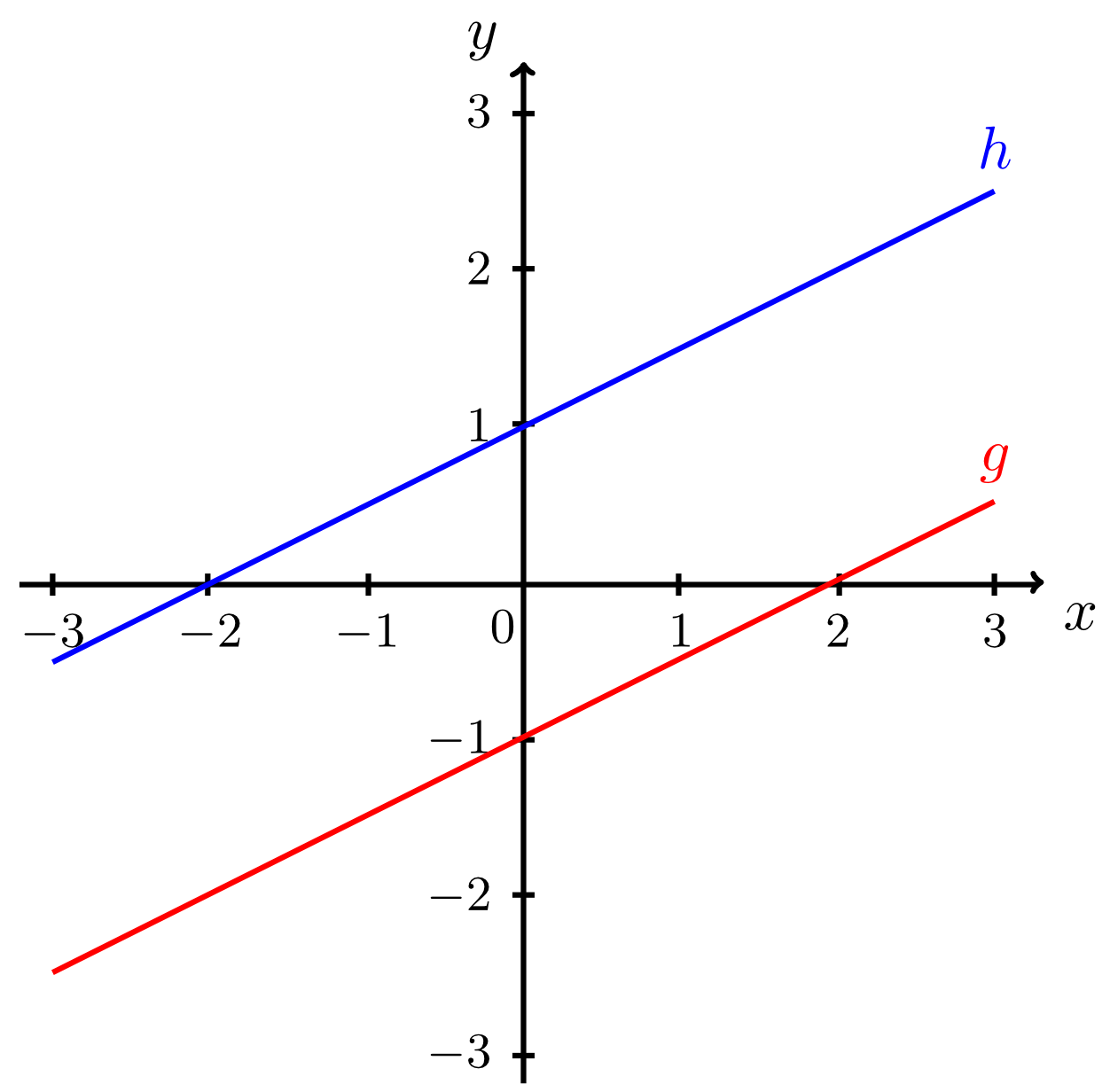
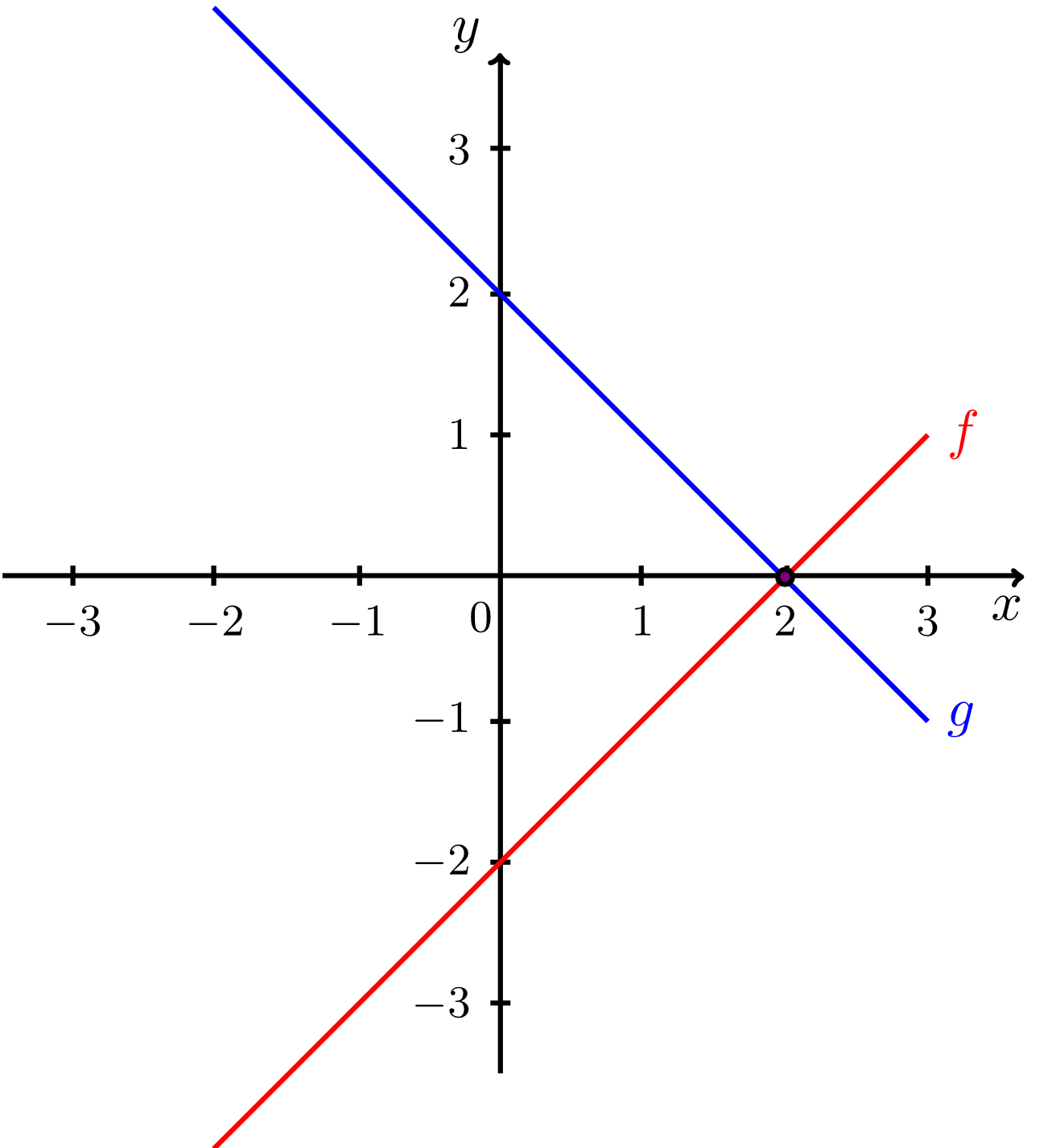
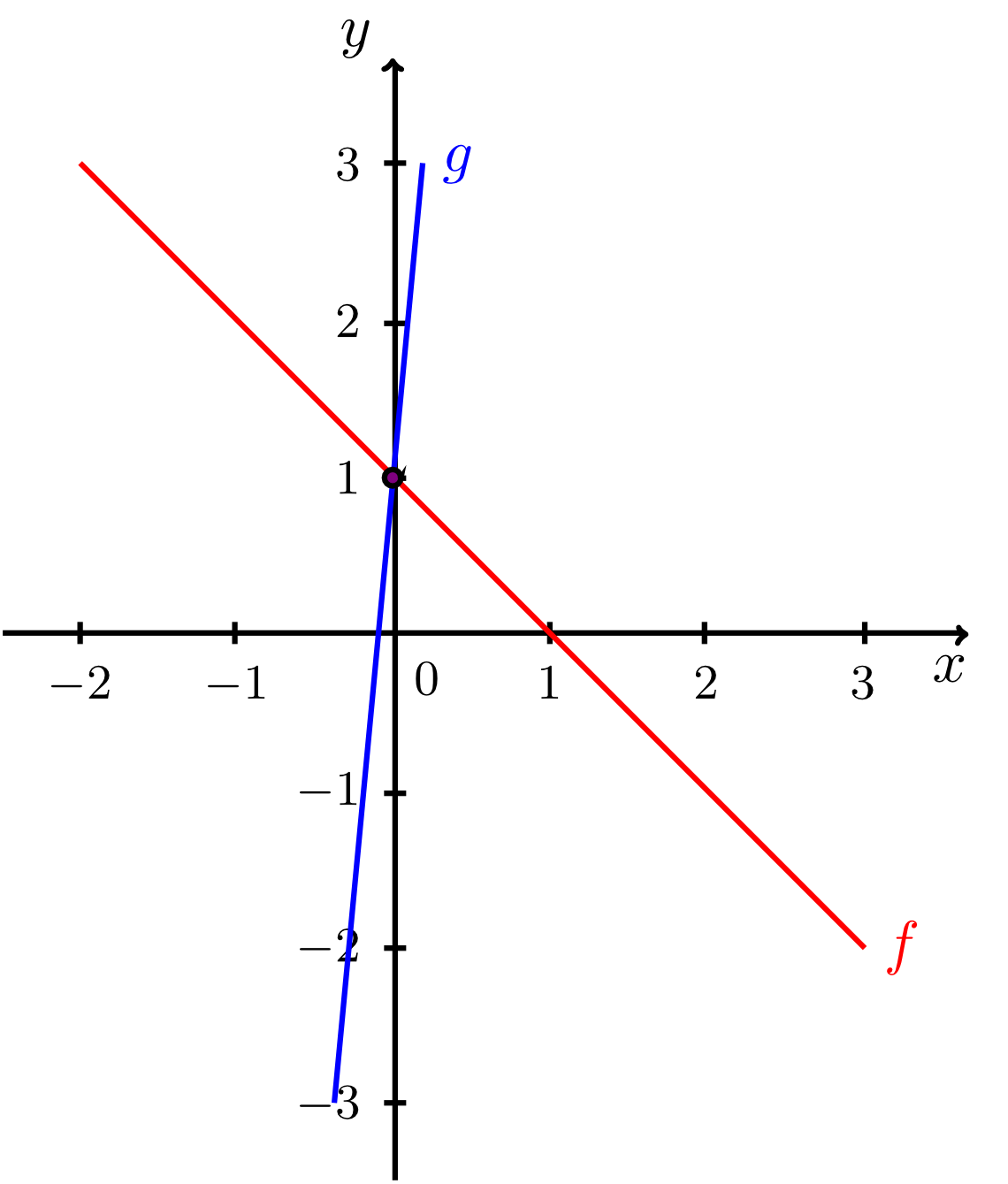
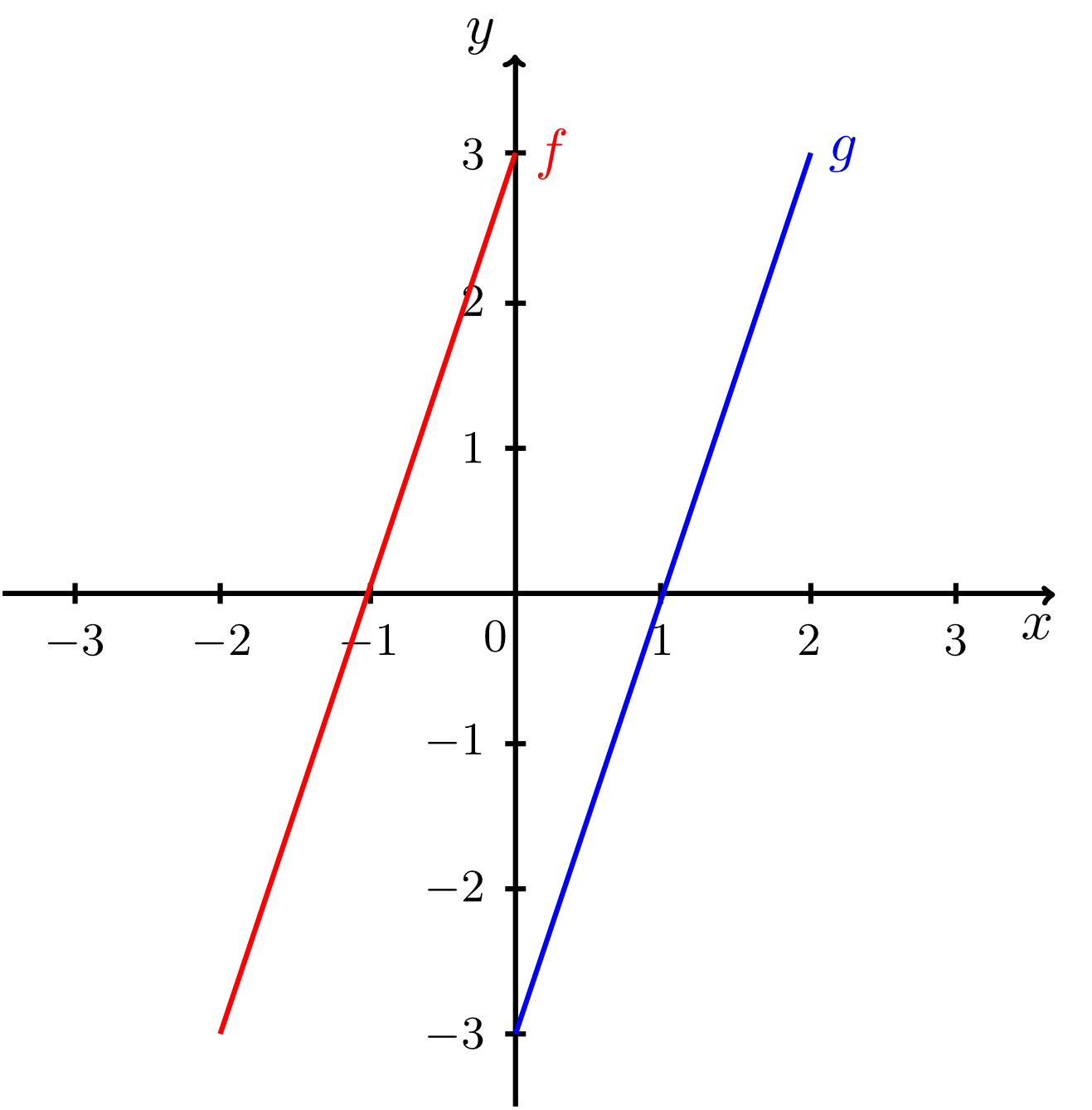
Exercise 9.2.18
Decide by calculation whether the given lines intersect. Tick the corresponding boxes and enter the intersection points for the lines that do intersect. Sketch the pairs of lines.
  1. f: y=x-2 and g: y=2-x:
      do not intersect (are parallel),
      are coincident,
      have an intersection point.

  2. f: y=1-x and g: y=4·(3x+1)-x-3:
      do not intersect (are parallel),
      are coincident,
      have an intersection point.

  3. f: y=4(x+1)-x-1 and g: y=3x-3:
      do not intersect (are parallel),
      are coincident,
      have an intersection point.

  4. f: y=5x-2 and g: y=(2x+1)+(3x-3):
      do not intersect (are parallel),
      are coincident,
      have an intersection point.

 
The first intersection point is
, the second intersection point is
.




: