9.4.1 Introduction

While in the previous sections curves in the plane (lines or circles) were investigated by means of coordinate equations, in this section we will replace the coordinate equations by coordinate inequalities. Thereby not curves but regions in the plane are described, which are bounded by the corresponding curves. Depending on whether the inequality is strict ($<$ or $>$) or not ($\le$ or $\ge$), the bounding curve is a part of the region or not. Regions can be, for example, areas above and below lines, areas within or outside circles, or even intersections of these. A few examples are shown in the figures below.

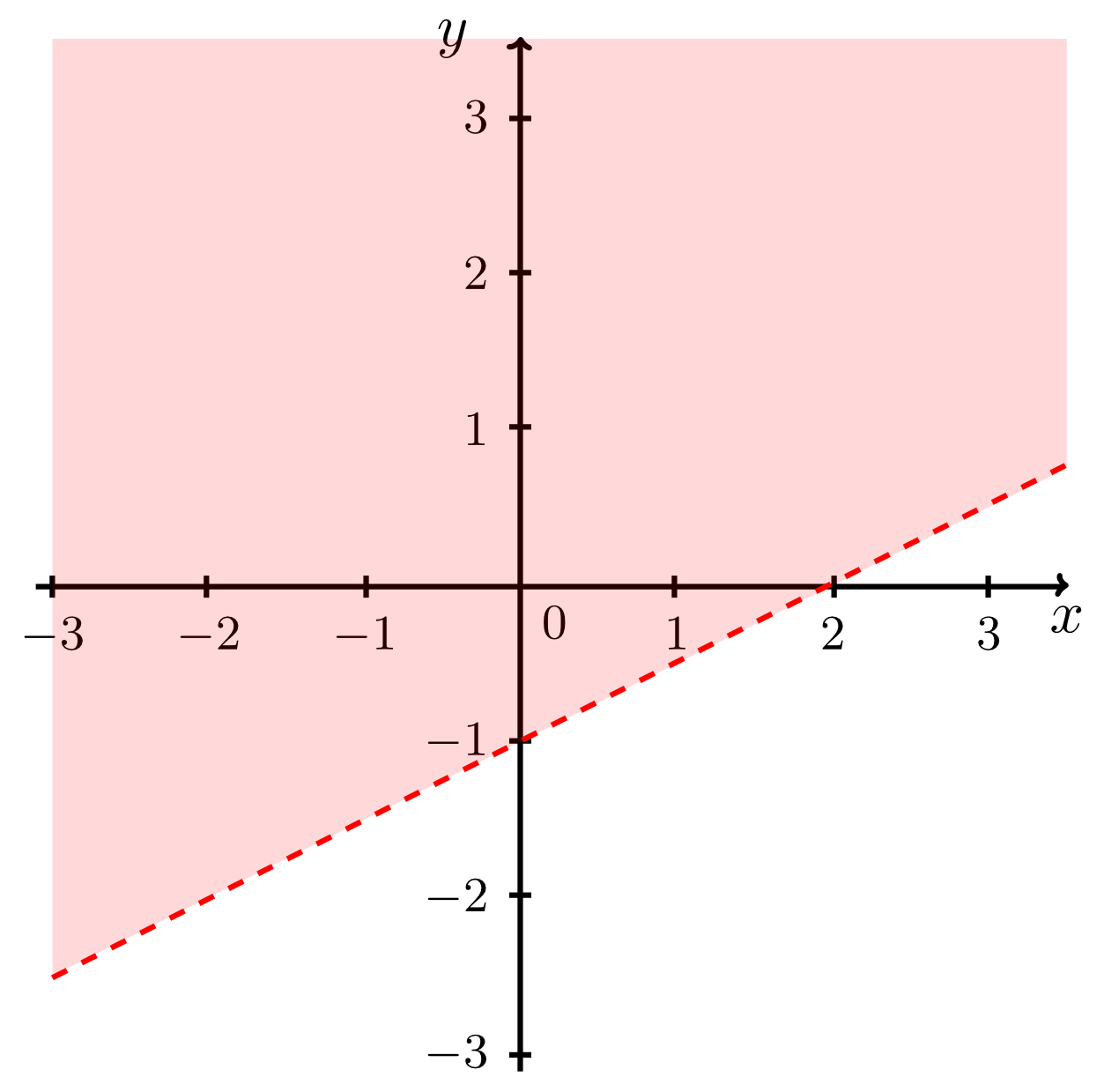
• Region above the line $y=\frac{1}{2}x-1$ excluding the line itself:
  
  
  
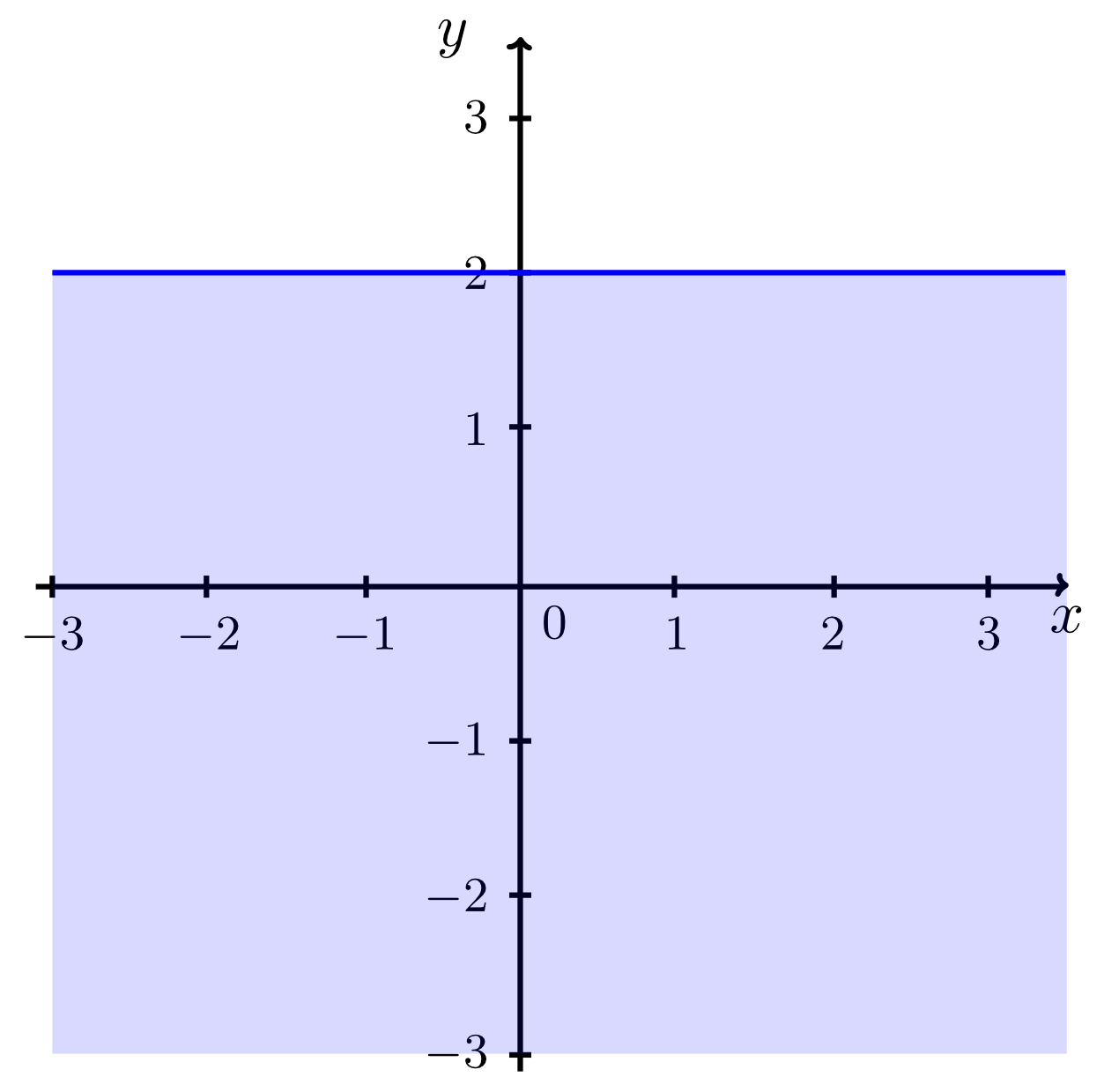
• Region below the line $y=2$ including the line itself:
  
  
  
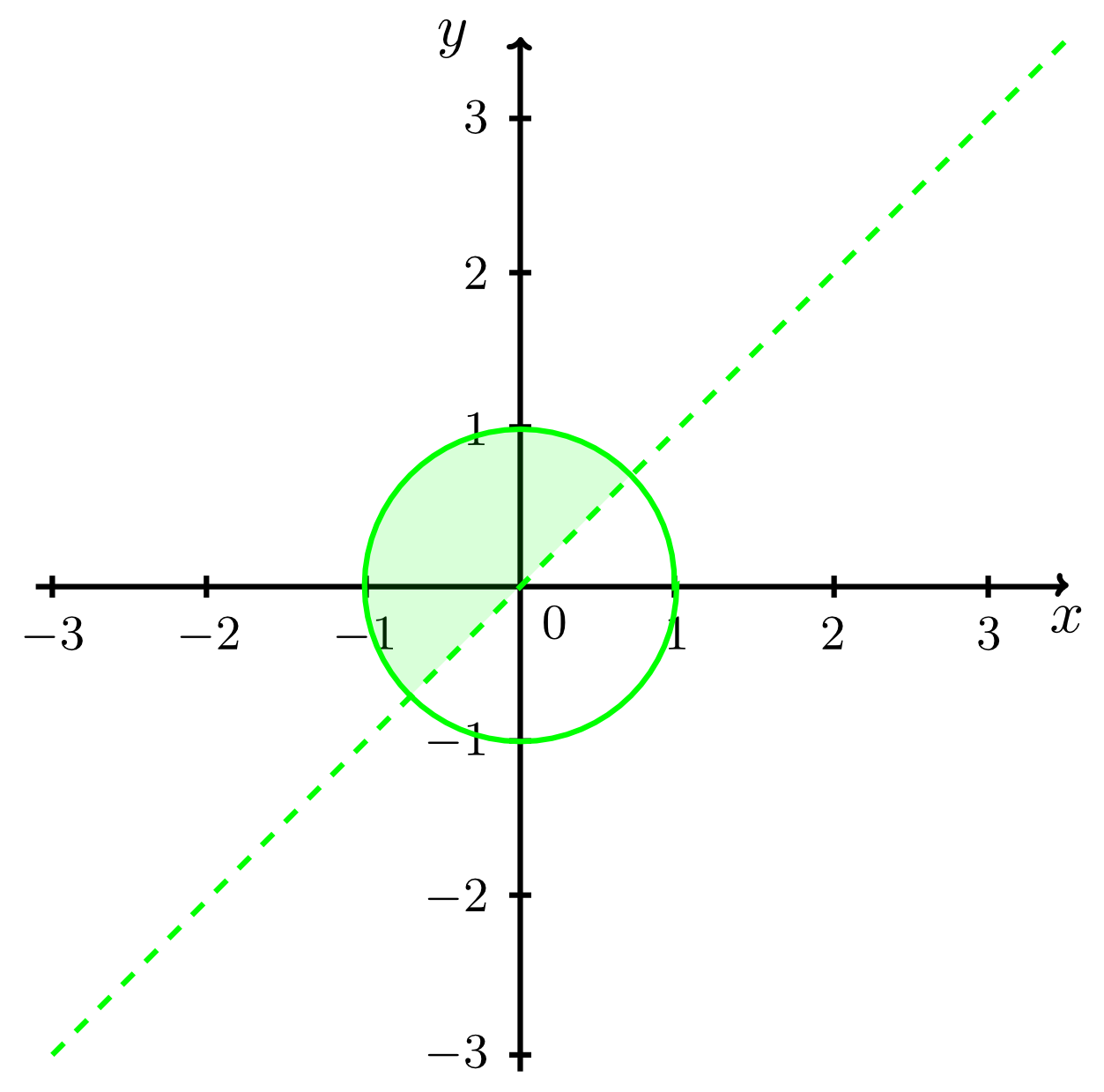
• Region above the line $y=x$ and within the unit circle $x^2+y^2=1$ including the points on the circle but excluding the points on the line:
  
  
  

Here and in the following we will use the general convention that curves included in the region are drawn as solid lines and curves excluded from the region are drawn as dashed lines.