Chapter 9 Objects in the Two-Dimensional Coordinate System
Section 9.3 Circles in the Plane9.3.4 Relative Positions of Circles
We may also raise the question of the relative position in the coordinate system for a circle and a line or for two circles, as we did for two lines. That is, we have to determine whether the two objects intersect, osculate (touch in a single point), or do not have any points in common. In the case of a circle and a line, the intersection point or the osculation point can be calculated easily. For two circles, this is more difficult and goes beyond the scope of this course. For two circles we will only discuss whether or not they intersect or osculate, not at which points this happens.
Info 9.3.9
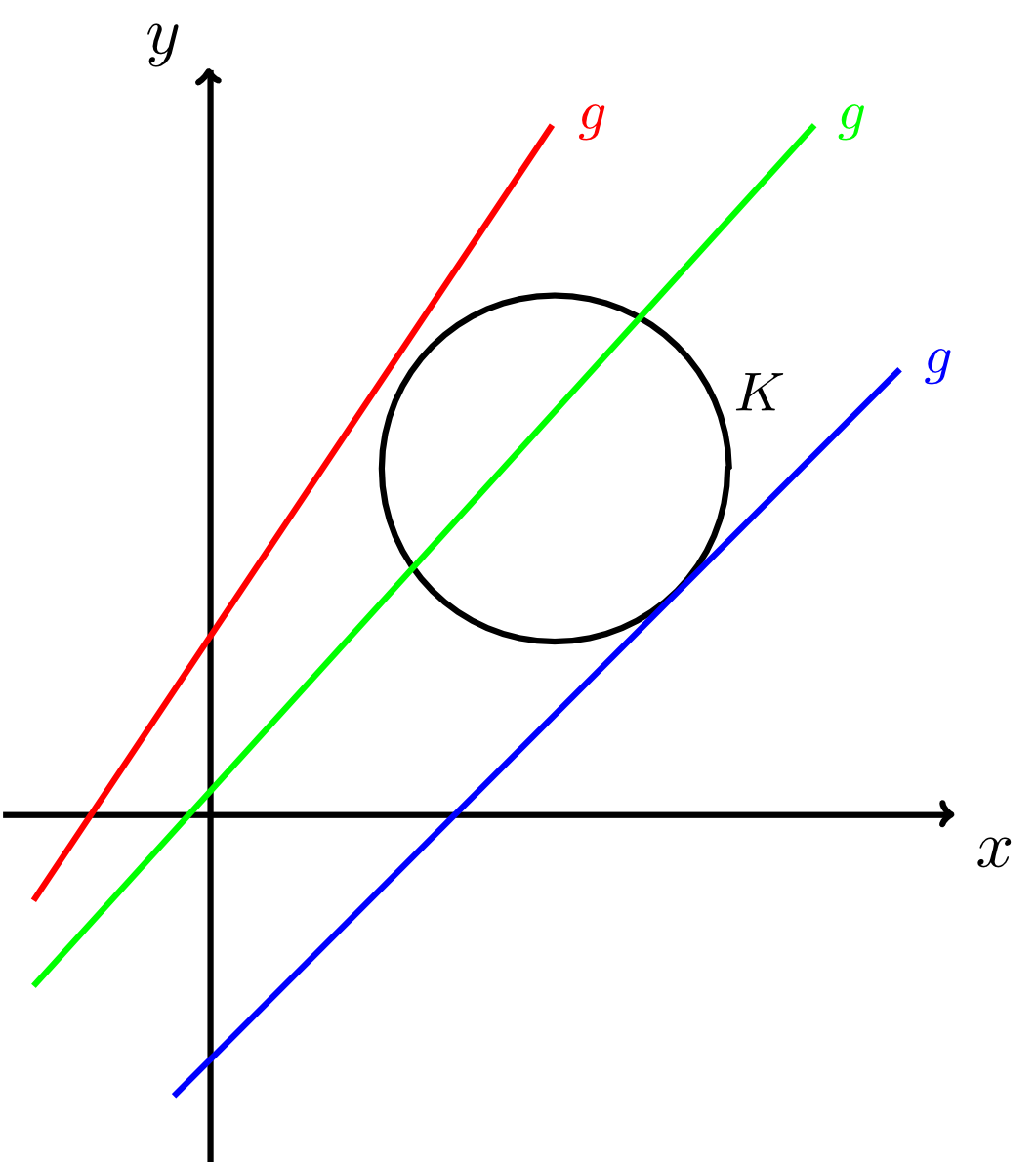
Let a circle and a line in the plane be given (by equations in coordinate form with respect to a fixed coordinate system). Then the circle and the line have exactly one of the following three relative positions with respect to each other.
- The circle and the line do not have any points in common. This is true for the red line in the figure below. Such a line is called an exterior line to the circle.
- The circle and the line have exactly one point in common, i.e. the line osculates the circle. This is true for the blue line in the figure below. Such a line is called a tangent line to the circle.
- The circle and the line have two points in common, i.e. the line intersects the circle. This is true for the green line in the figure below. Such a line is called a secant line to the circle.
If a line is a tangent or a secant, the circle and the line have one or two points in common, respectively. How can the intersection point or points be calculated? Since the points lie on both the circle and on the line, they have to satisfy both the equation of the circle and the equation of the line in coordinate form. Thus, we have two equations for the two unknown coordinates of the intersection points, and we are able to calculate the coordinates. However, since in the equations of a circle in coordinate form the unknown coordinates are squared, we do not have two linear equations. Hence, the methods for solving systems of linear equations described in Module 5 unfortunately cannot be applied. The Info Box below outlines the method for calculating the intersection points.
Info 9.3.10
Let a circle in the plane with centre and radius be given by an equation of a circle in coordinate form
and a line with slope and -intercept by an equation in normal form
To calculate the potential intersection points, the equation of can be substituted into the equation of resulting in a quadratic equation in the variable :
For a quadratic equation three cases can occur (see Section 2.1.5):
- The quadratic equation has no solution. In this case, is an exterior line to . An -coordinate of a common point cannot be found.
- The quadratic equation has exactly one solution. In this case, is a tangent line to . For the -coordinate (the solution of the quadratic equation), a corresponding -coordinate can be calculated from the given equation of a line. The two coordinates define the osculation point of the tangent line and the circle .
- The quadratic equation has two solutions. In this case, is a secant line to . For both -coordinates (the two solutions of the quadratic equation), corresponding -coordinates can be calculated from the given equation of a line. The two pairs of coordinates define the intersection points of the secant line and the circle .
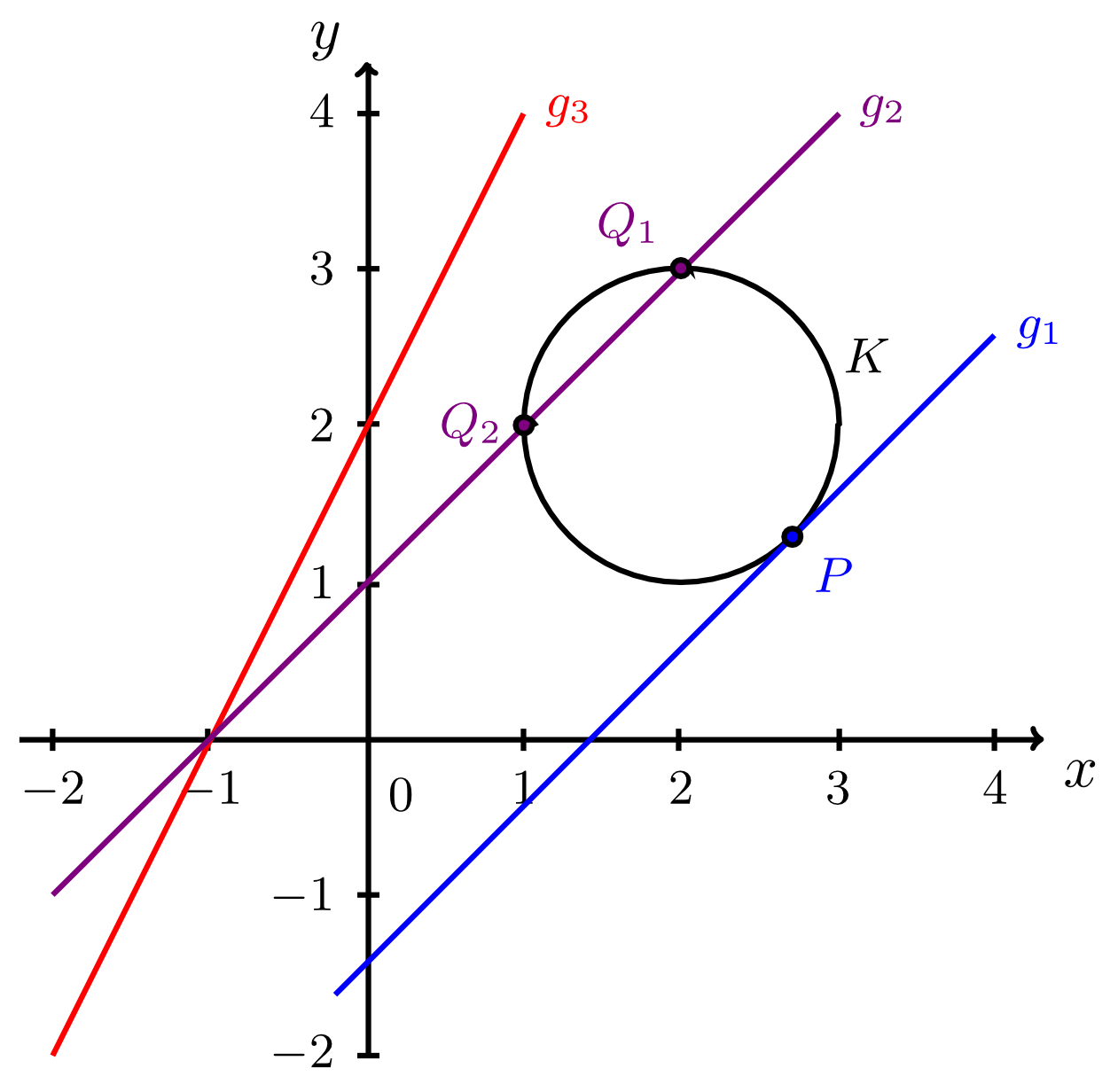
Example 9.3.11
Let a circle with the centre and a radius of be given by
and the lines , , and by
and the lines , , and by
- Line :
Substituting the equation of the line into the given equation of the circle results in
The resulting quadratic equation has only the solution . Thus, is a tangent line to that osculates in a point with the -coordinate . The corresponding -coordinate is calculated from the given equation of the line:
Thus, the tangent line osculates the circle at the point .
- Line :
Substituting the equation of the line into the given equation of the circle results in
The resulting quadratic equation has two solutions. Thus, is a secant line to the circle that intersects in two points with the -coordinates and . The corresponding -coordinates are calculated from the given equation of the line:
Thus, the two points and are the intersection points of the secant line with the circle .
- Line :
Substituting the equation of the line into the given equation of the circle results in
The discriminant (see Section 2.1.5) of this quadratic equation is
Thus, the equation does not have a solution, and the line is an exterior line to the circle .
Exercise 9.3.12
Let a circle be given by the equation
and two lines by
and two lines by
- Show that is a tangent line to , and calculate the -coordinate and -coordinate of the osculation point of and .
- Show that is a secant line to , and calculate the -coordinates and -coordinates of the intersection points and of and .
Exercise 9.3.13
Let a circle be given by the equation
and the line with the slope and the -intercept by the equation
in normal form. Find the interval in which must lie such that is a secant line to .
.
Enter square roots as sqrt. Enter, for example, sqrt(2) as .
and the line with the slope and the -intercept by the equation
in normal form. Find the interval in which must lie such that is a secant line to .
.
Enter square roots as sqrt. Enter, for example, sqrt(2) as .
Of course, lines defined by equations that cannot be transformed into normal form (i.e. lines that are parallel to the -axis) can intersect or osculate circles as well. The method described above cannot be applied directly to such lines . The example below illustrates the method which is applied in this case.
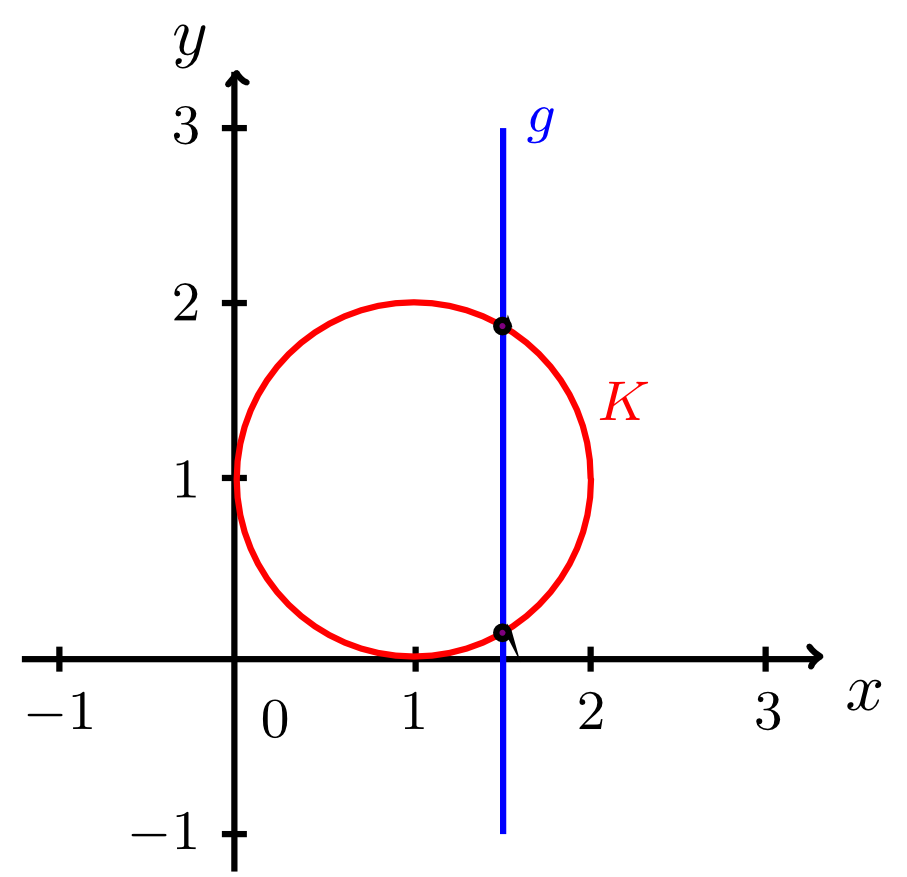
Example 9.3.14
Let a circle be given by the equation
and line by the equation
The two objects are shown in the figure below. Obviously, is a secant line to . In this case, the intersection point cannot be calculated by solving the equation of a line for . Instead, the equation of a line is simply substituted into the given equation of a circle. This results in two values of , i.e. the -coordinates of the intersection points:
Obviously, both corresponding -coordinates are equal to since the intersection points lie on the line . Thus, the two intersection points of the line and the circle are and .
and line by the equation
The two objects are shown in the figure below. Obviously, is a secant line to . In this case, the intersection point cannot be calculated by solving the equation of a line for . Instead, the equation of a line is simply substituted into the given equation of a circle. This results in two values of , i.e. the -coordinates of the intersection points:
Obviously, both corresponding -coordinates are equal to since the intersection points lie on the line . Thus, the two intersection points of the line and the circle are and .
The Info Box below lists the different cases for the relative positions of two circles together with general criteria that allow to decide which of the cases for two given circles applies.
Info 9.3.15
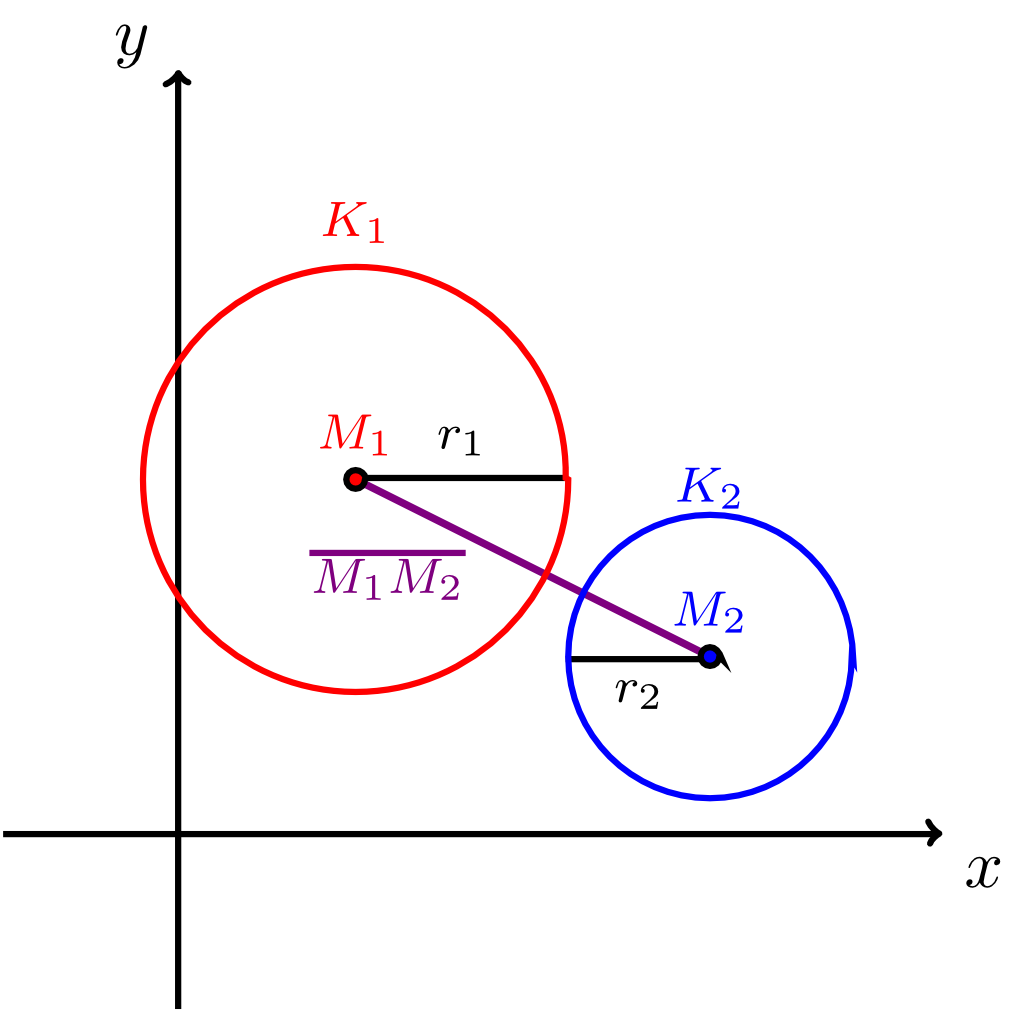
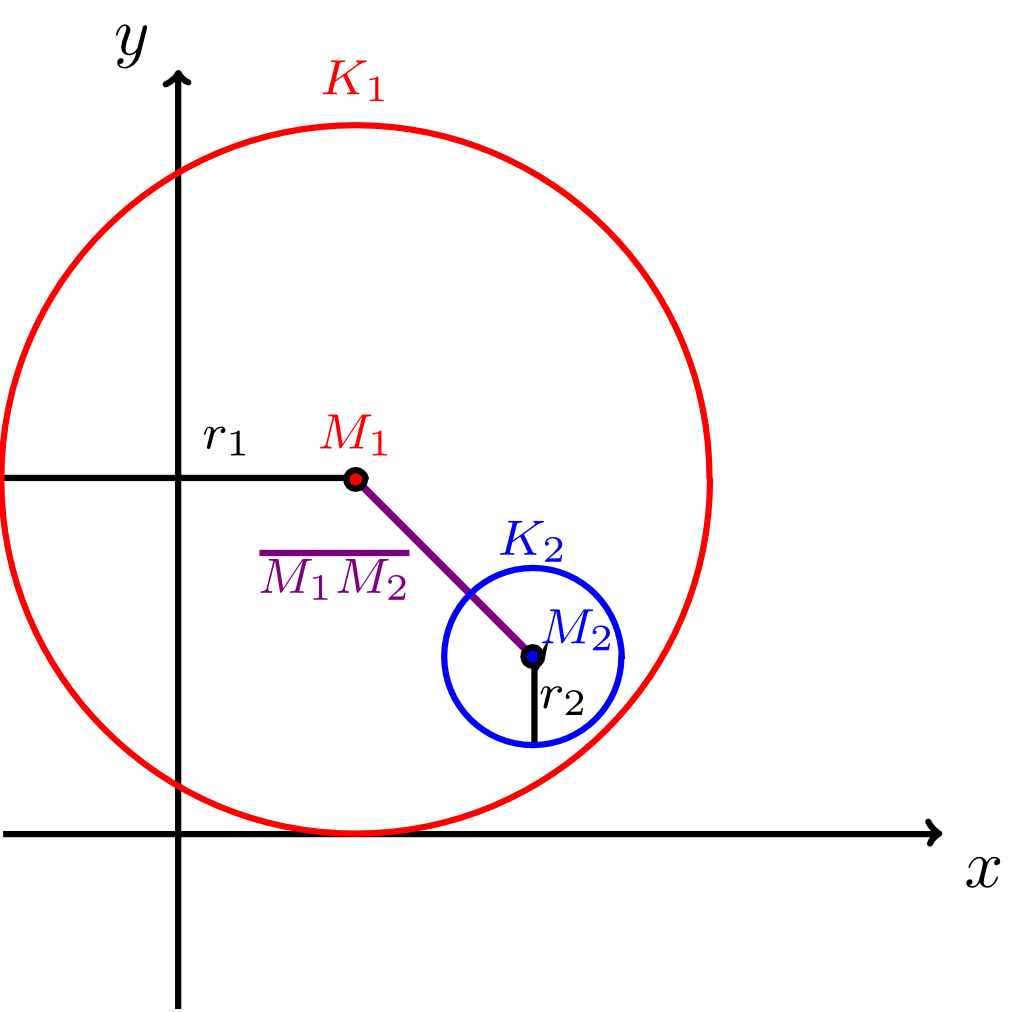
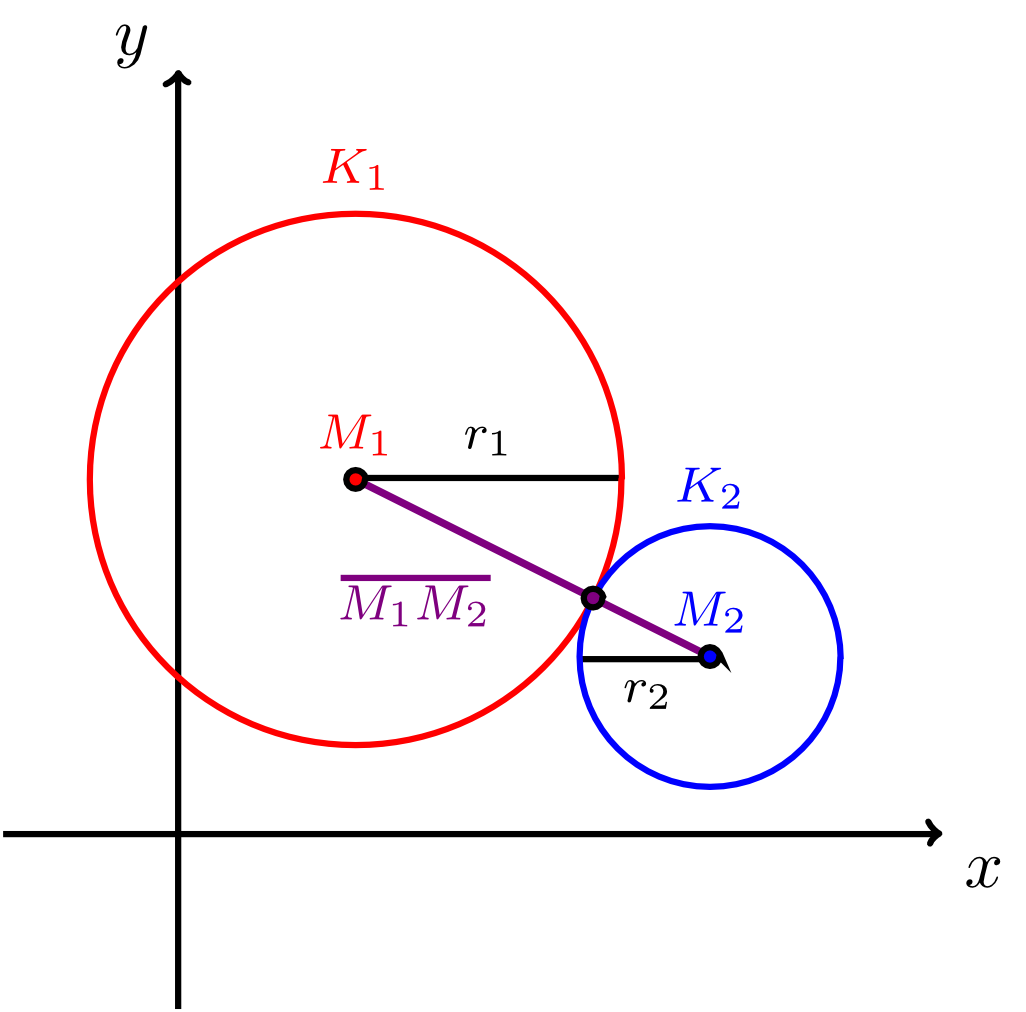
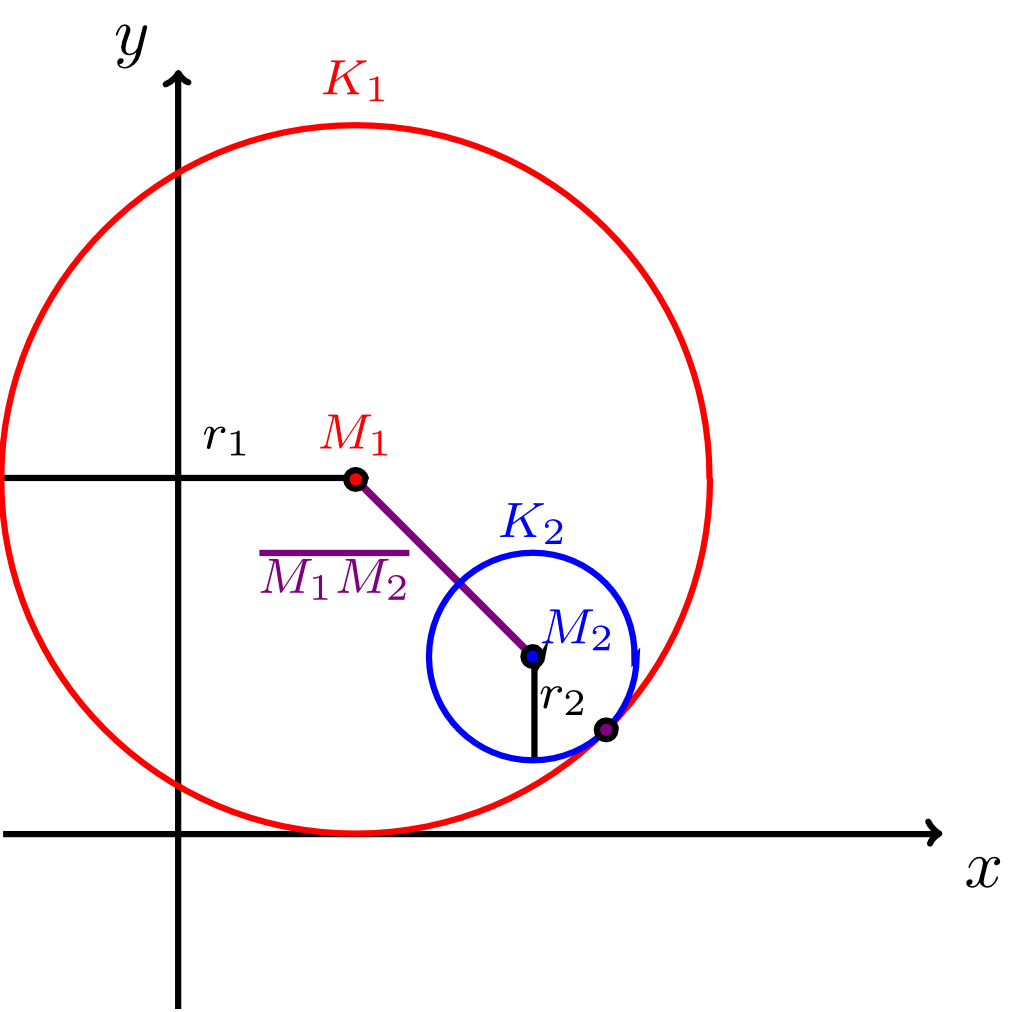
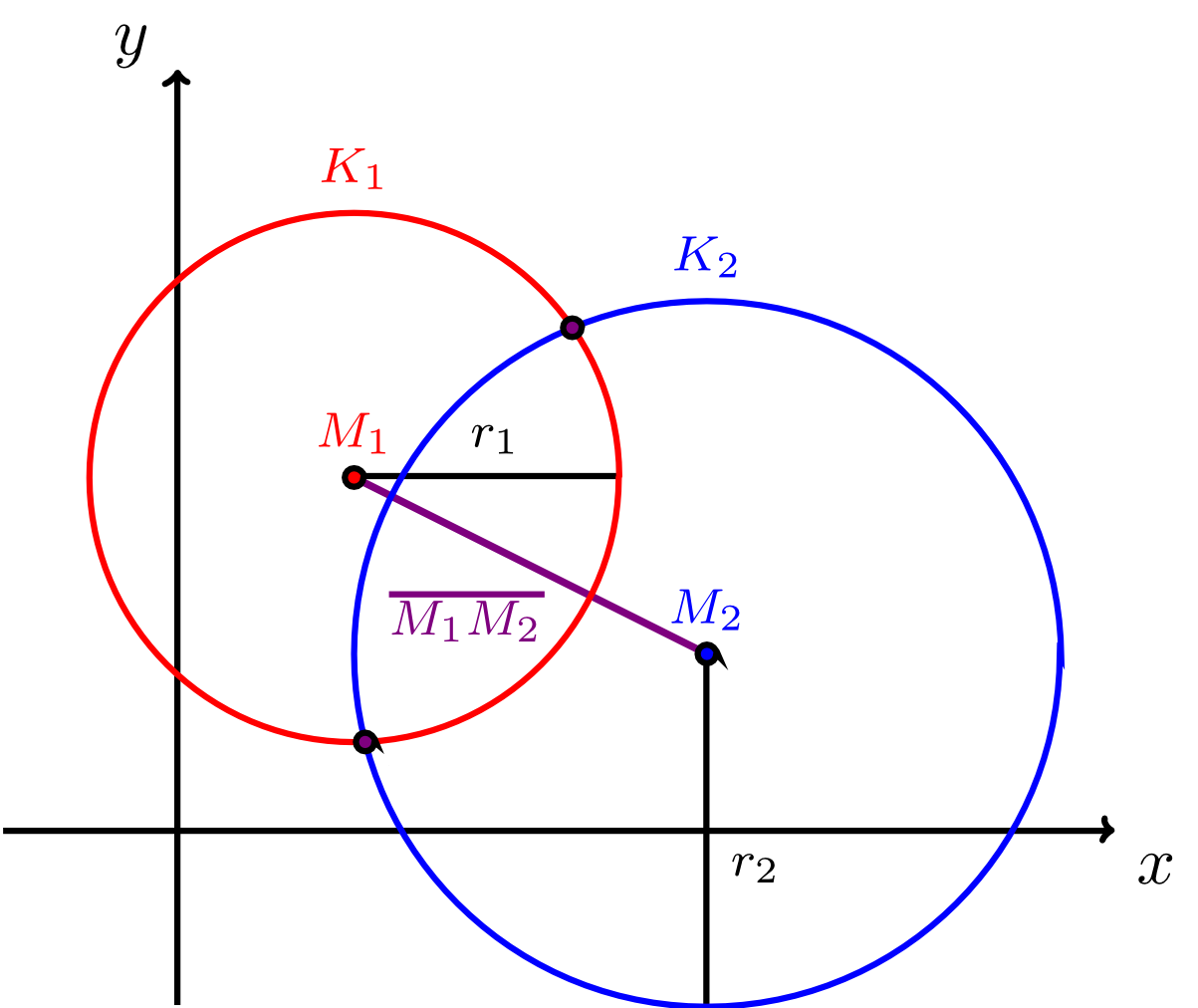
Let two (different) circles, with centre and radius and with centre and radius , be given (by equations of a circle in the plane with respect to a fixed coordinate system). Then the circles have exactly one of the following three relative positions with respect to each other:
- The circles and do not have any points in common, i.e. they do not intersect. This is the case if and only if for the radii and and the distance of the two centres, we have the inequalities
- The circles and have one point in common, i.e. they osculate. This is the case if and only if for the radii and and the distance of the two centres, we have the inequalities
- The circles and have two points in common, i.e. they intersect. This is the case if and only if for the radii and and the distance of the two centres, we have the inequality
Thus, the relative position of two circles can be determined from their centres and radii. The calculation of possible intersection points is more difficult and goes beyond the scope of this course.
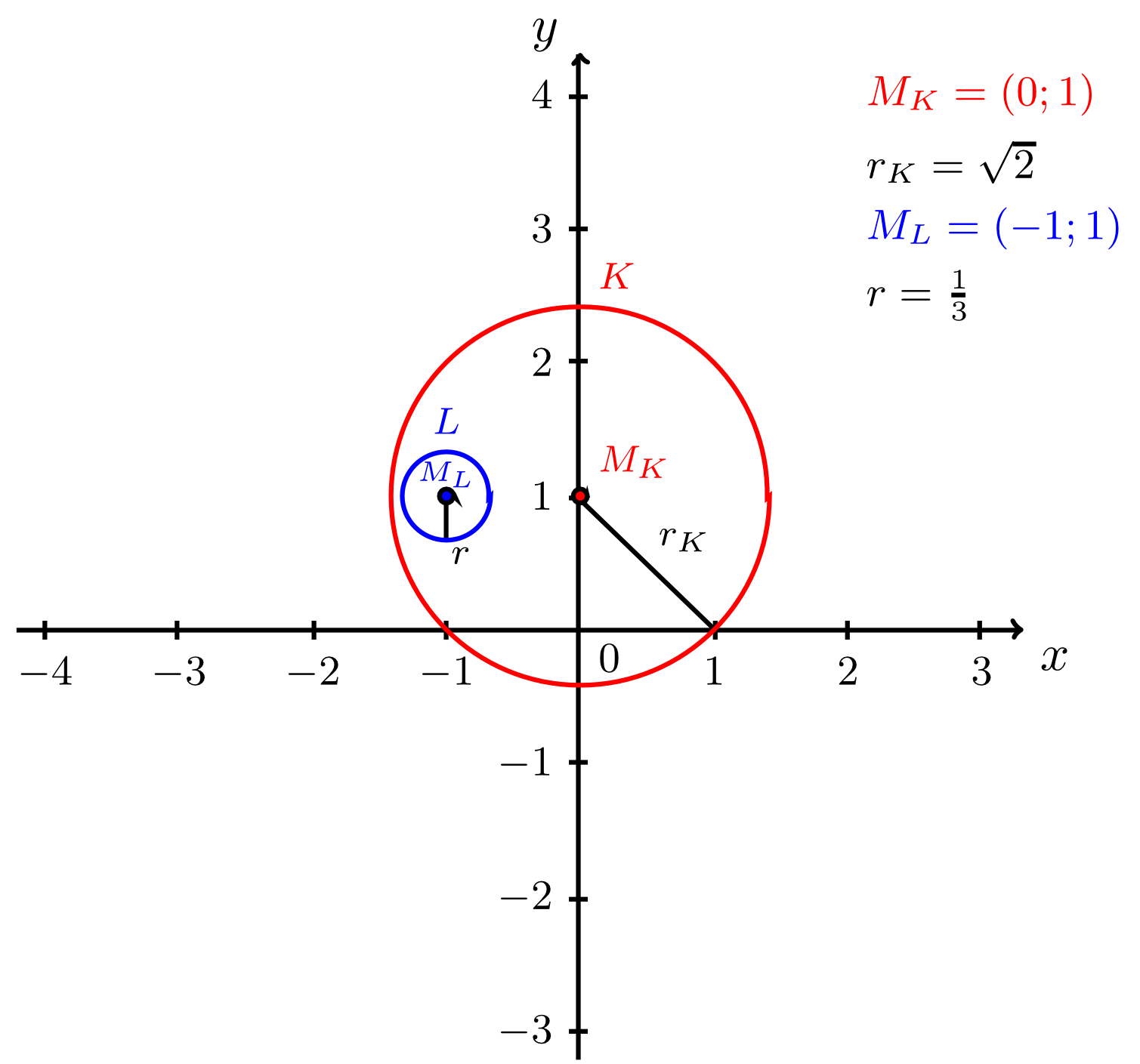
Example 9.3.16
Let a circle with centre and radius be given by the equation
and a circle with centre and unknown radius by the equation
Find the values of for which the circles and intersect, osculate, or do not intersect.
From the given equation of a circle the centre can be read off directly: . However, the equation for is not in normal form. By completing the square this equation can easily be transformed into normal form such that the centre and the radius can be read off:
Thus, we have and . Hence, the distance between the two centres is
and the sum of the two radii is
Since , we have
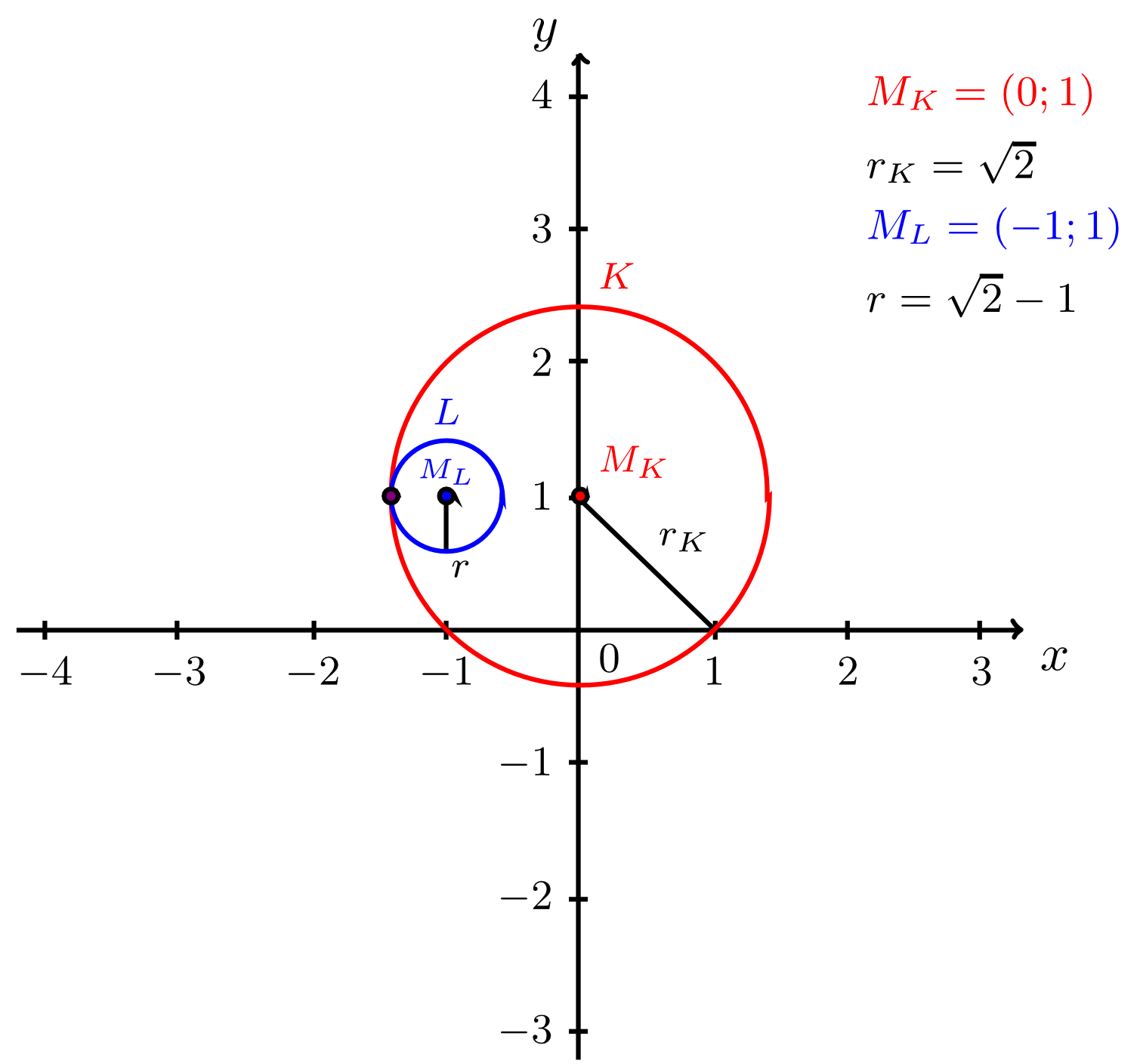
Hence cannot occur in this case. The geometric reason for this is that the centre of lies within , as can be seen from the figure below. According to the criteria listed in Info Box 9.3.15, the two circles osculate if
According to the section on absolute value inequalities, this equation is satisfied if
Hence, the two radii for which the circle osculates the circle are:
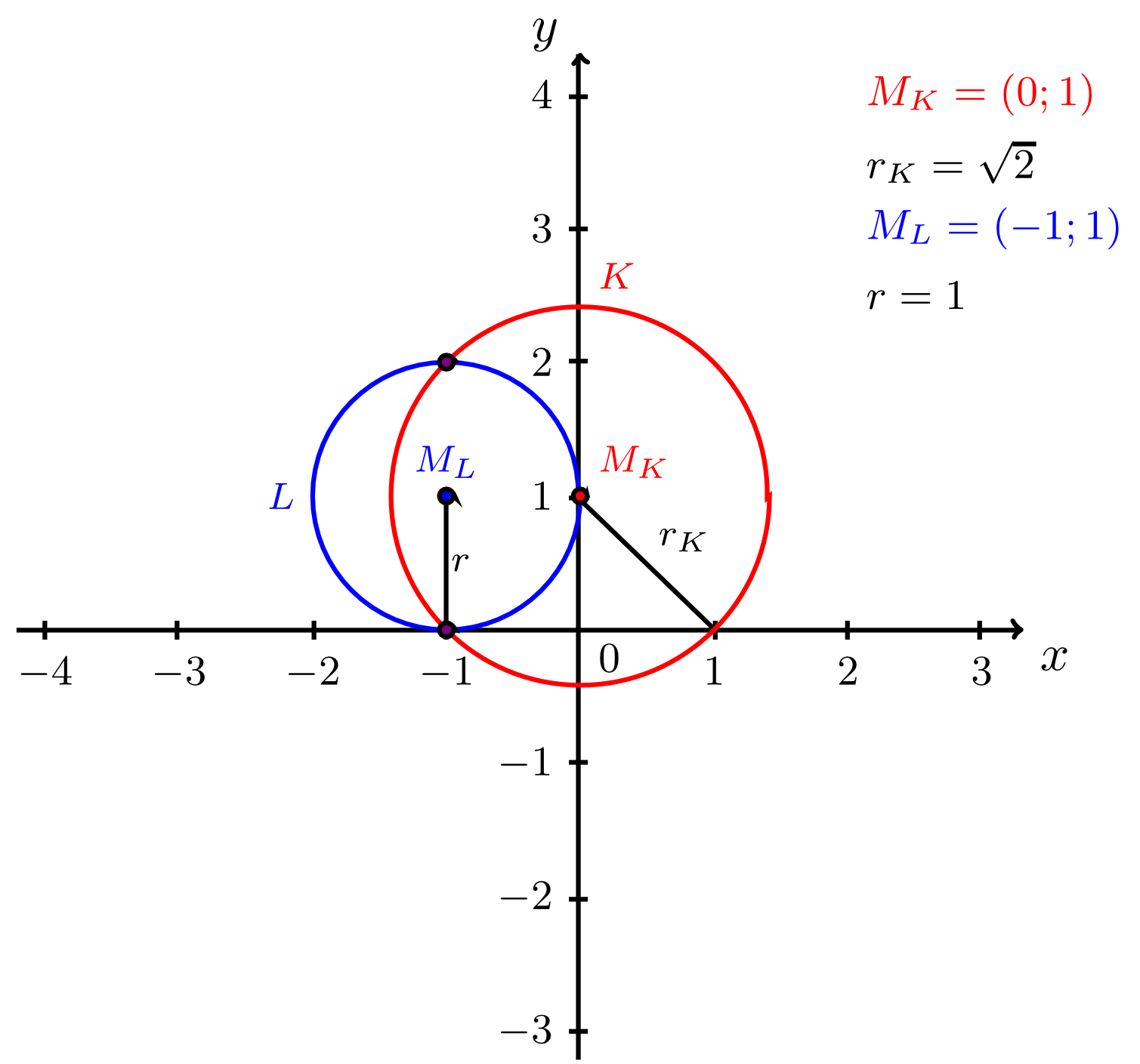
Now we have still to investigate the remaining possible values of . For , we have
i.e. and do not have any points in common. For , we have to distinguish the cases and if we investigate the absolute value. In the case , we have
and in the case , we have
Thus, the circles and have two points in common for , i.e. the circles intersect. Finally, we have in the case :
The circles and also do not have any points in common in this case. In summary, we have the following conditions for the relative position of the two circles and :
and a circle with centre and unknown radius by the equation
Find the values of for which the circles and intersect, osculate, or do not intersect.
From the given equation of a circle the centre can be read off directly: . However, the equation for is not in normal form. By completing the square this equation can easily be transformed into normal form such that the centre and the radius can be read off:
Thus, we have and . Hence, the distance between the two centres is
and the sum of the two radii is
Since , we have
Hence cannot occur in this case. The geometric reason for this is that the centre of lies within , as can be seen from the figure below. According to the criteria listed in Info Box 9.3.15, the two circles osculate if
According to the section on absolute value inequalities, this equation is satisfied if
Hence, the two radii for which the circle osculates the circle are:
Now we have still to investigate the remaining possible values of . For , we have
i.e. and do not have any points in common. For , we have to distinguish the cases and if we investigate the absolute value. In the case , we have
and in the case , we have
Thus, the circles and have two points in common for , i.e. the circles intersect. Finally, we have in the case :
The circles and also do not have any points in common in this case. In summary, we have the following conditions for the relative position of the two circles and :
- If , the two circles and osculate at one point.
- If , the two circles and intersect at two points.
- If , the two circles and do not have any points in common.
Exercise 9.3.17
Let two circles and be given by the equations
The two circles and
The two circles and
| osculate at one point, | |
| intersect at two points, | |
| do not have any points in common. |
 Onlinebrückenkurs Mathematik
Onlinebrückenkurs Mathematik