9.2.1 Introduction

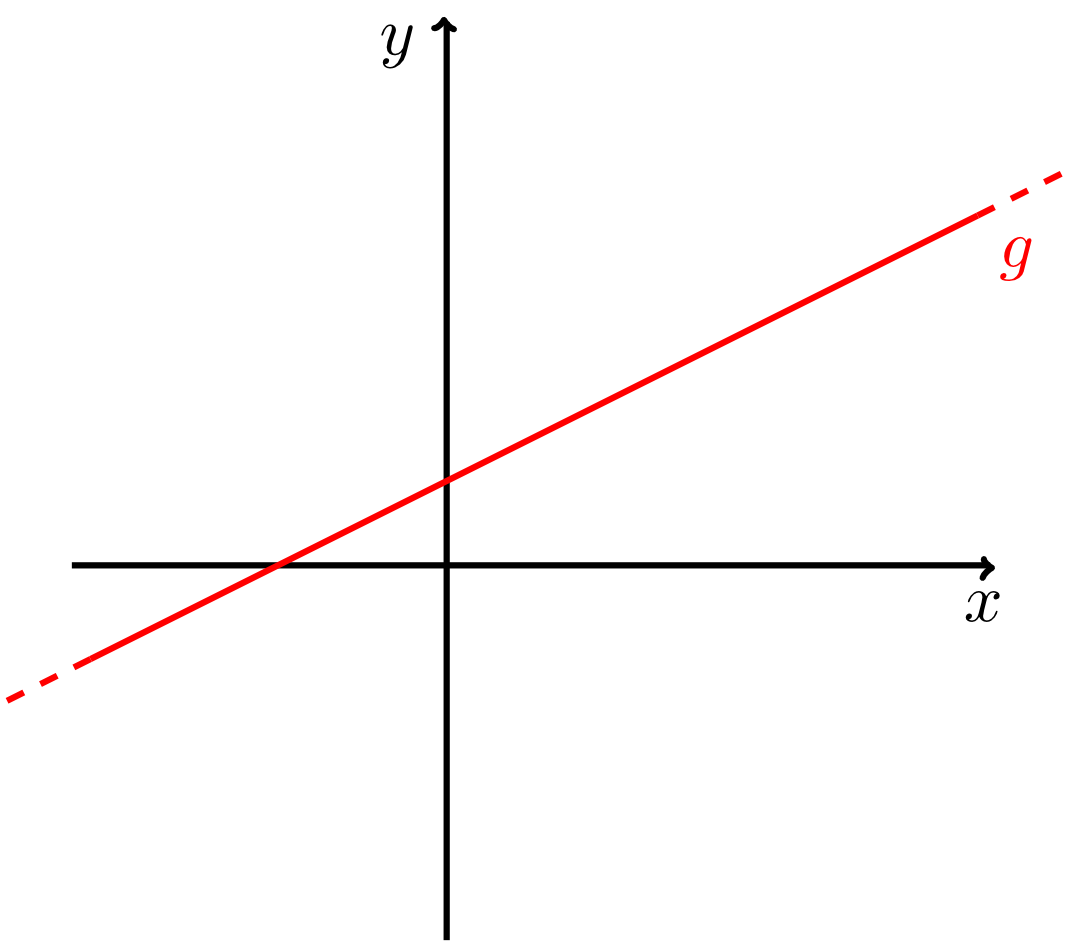
In Module 5, lines in the plane were defined as line segments that are continued on both ends indefinitely. In the context of the previous section, these lines can now be considered as infinite sets of points in the plane with respect to a Cartesian coordinate system. The elements of these sets of points then have to satisfy certain (linear) equations. Usually, lines are denoted by lowercase Latin letters $g,h,\dots$. If a line is drawn in a coordinate system, only a section or segment of the line can be drawn. However, the line itself extends indefinitely (see figure below).

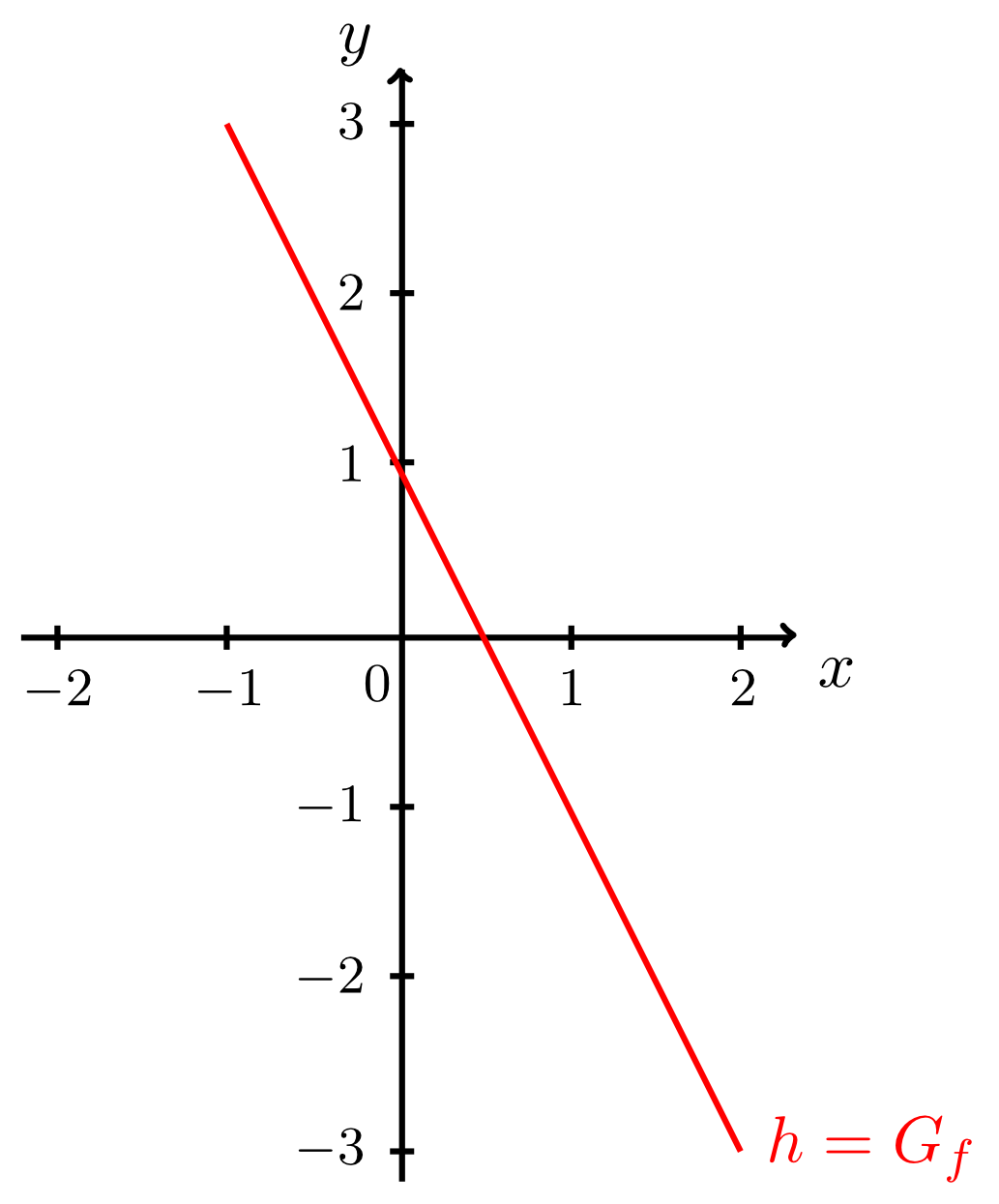
From Module 6 we already know special cases of lines that are described as infinite sets in $ℝ{}^2$. Namely, these are the graphs of linear affine functions that we discussed in Section Linear Functions and Polynomials in Module 6. The example below revises the relevant terms of this section before they are used again further on.