Chapter 9 Objects in the Two-Dimensional Coordinate System
Section 9.4 Regions in the plane9.4.2 Regions bounded by Lines and Circles
The Info Box below lists the regions that can occur if the equals sign in the equation of a line is replaced by an inequality sign.
Info 9.4.1
Let a line in the plane (with slope and -intercept ) be given by
in normal form with respect to a fixed coordinate system. Substituting an inequality sign for the equals sign results in the following sets that describe regions in the plane:
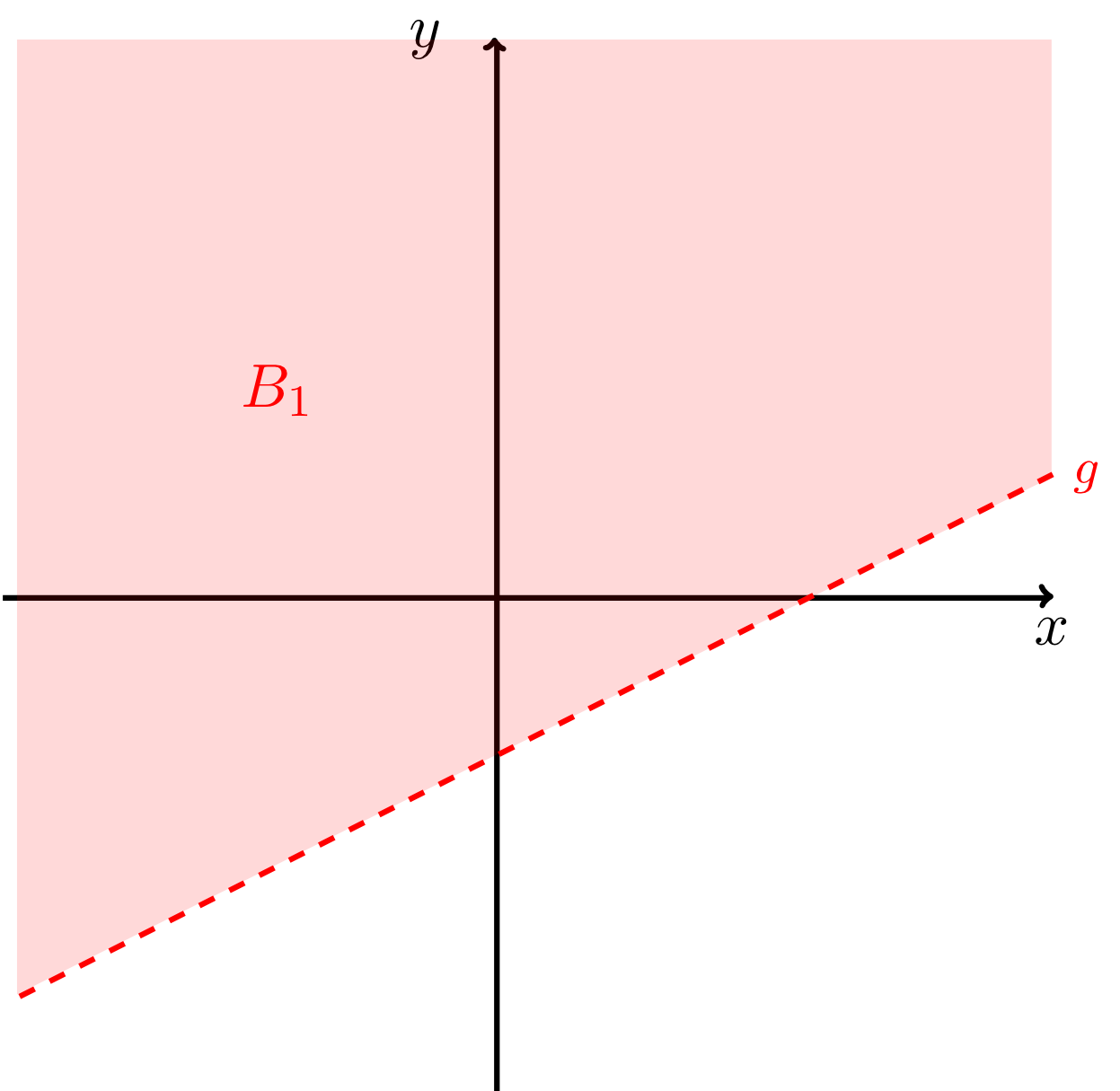
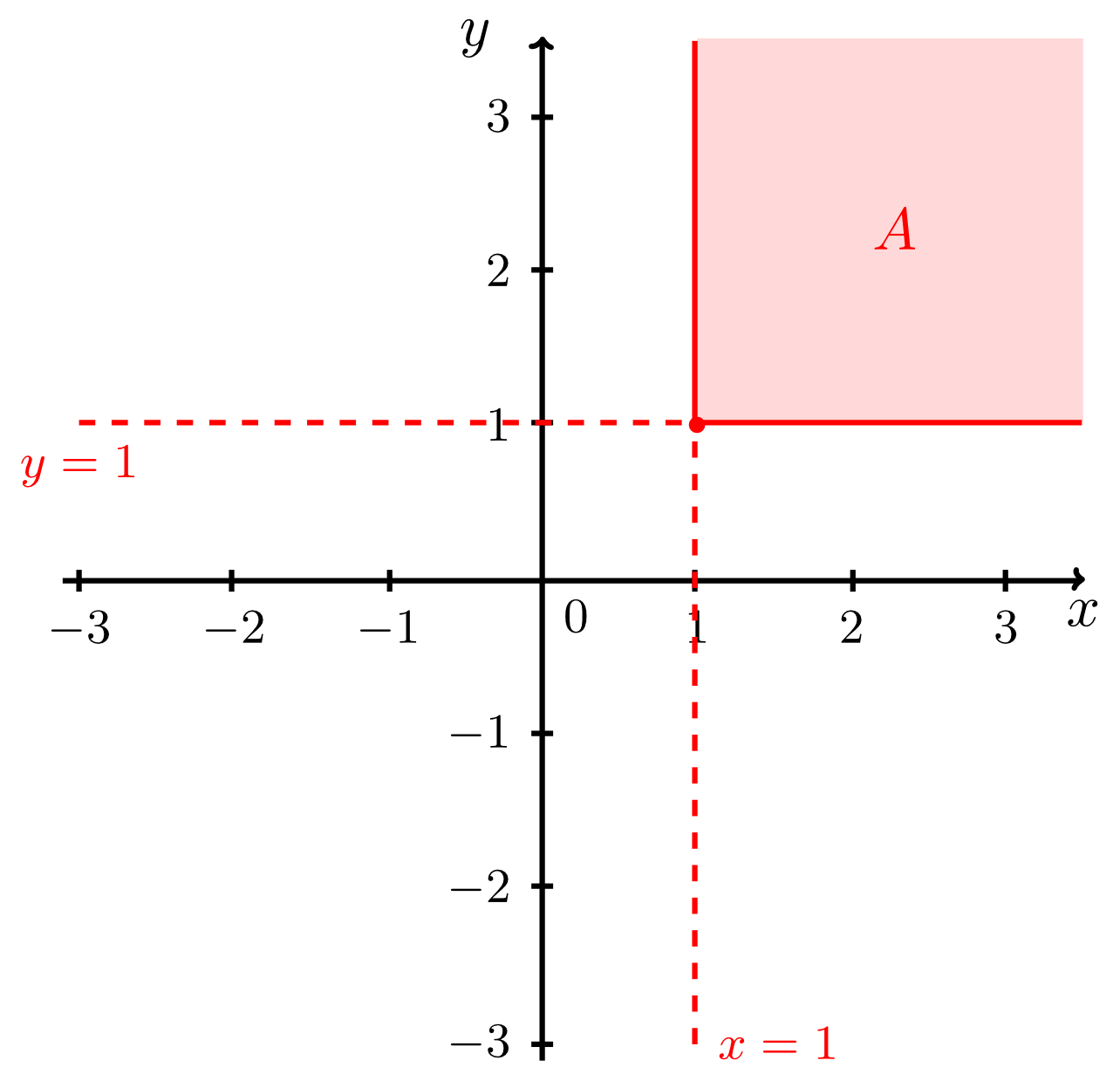
- "region above the line excluding the points on the line itself"
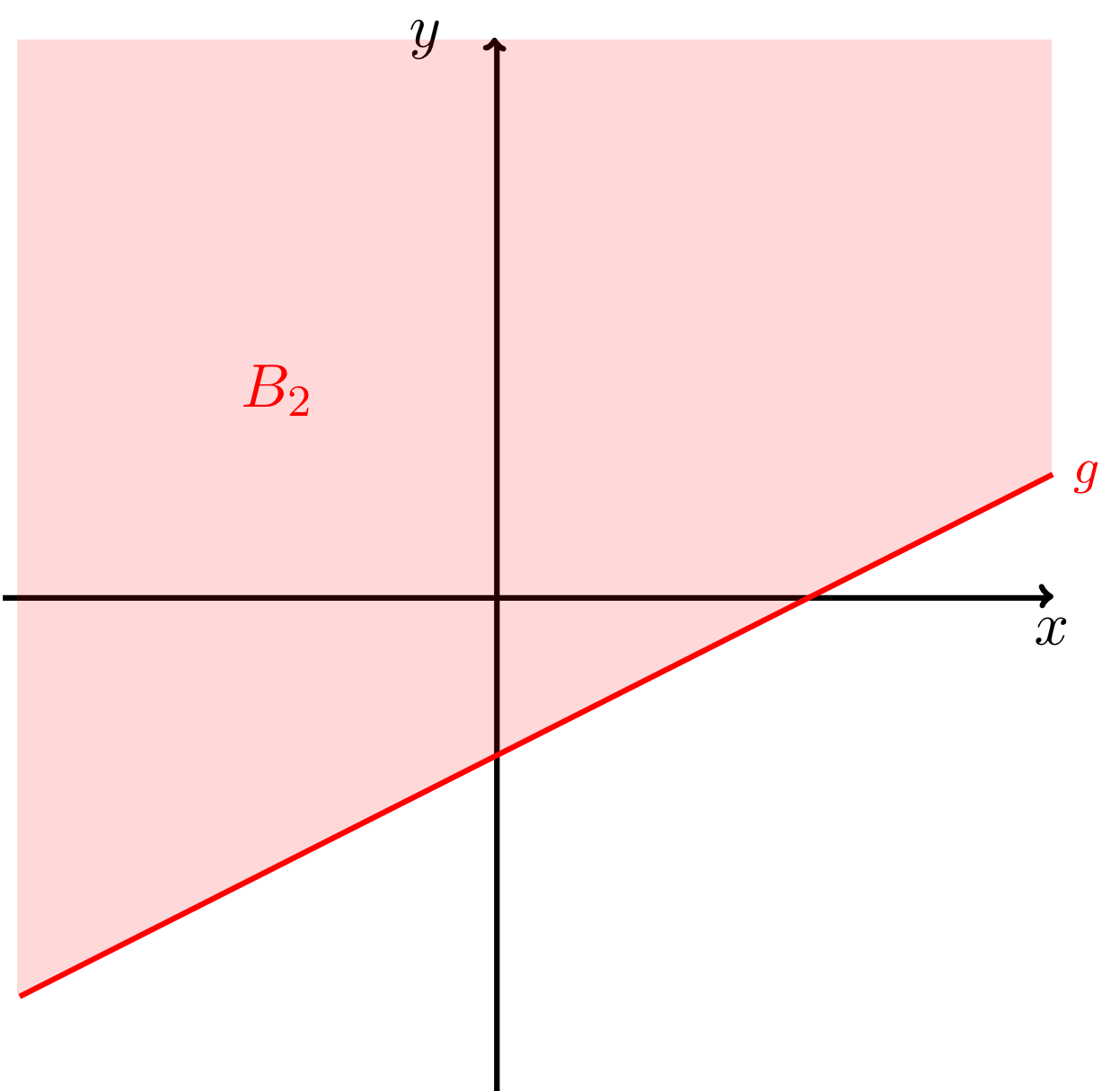
- "region above the line including the points on the line itself"
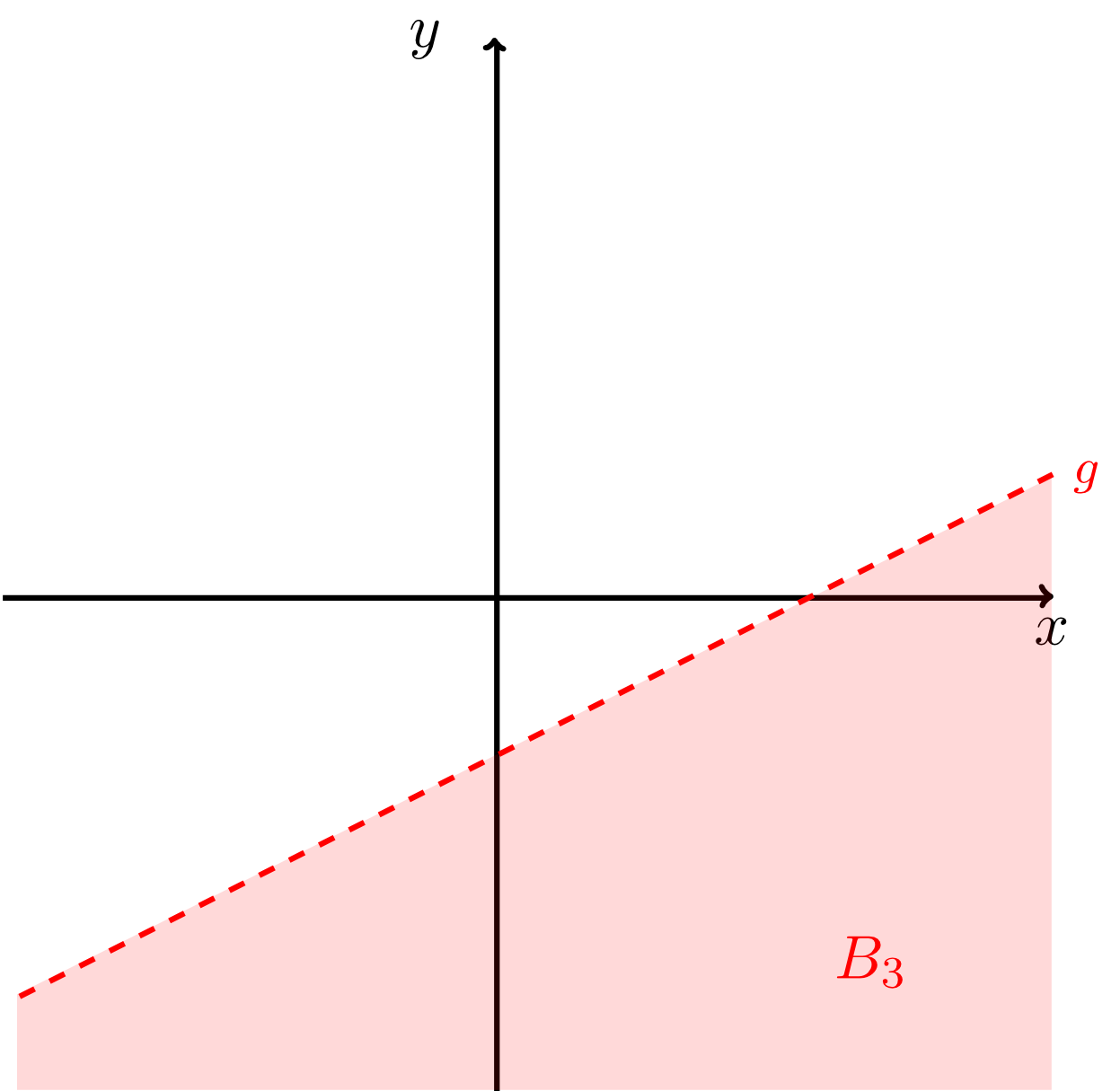
- "region below the line excluding the points on the line itself"
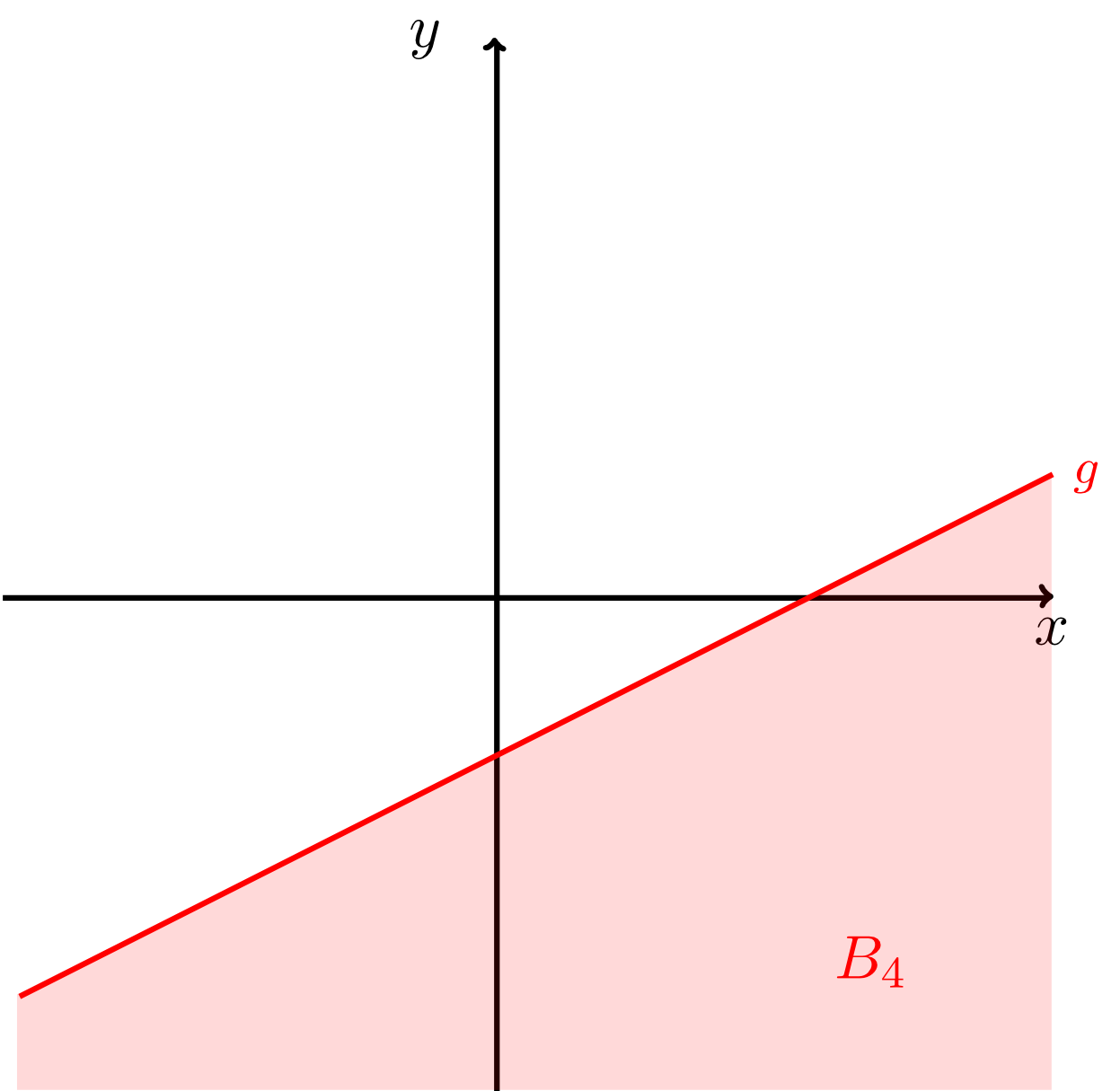
- "region below the line including the points on the line itself"
For equations of a line that cannot be transformed into normal form, the line of thought on the resulting regions is analogous. The example below shows two simple cases.
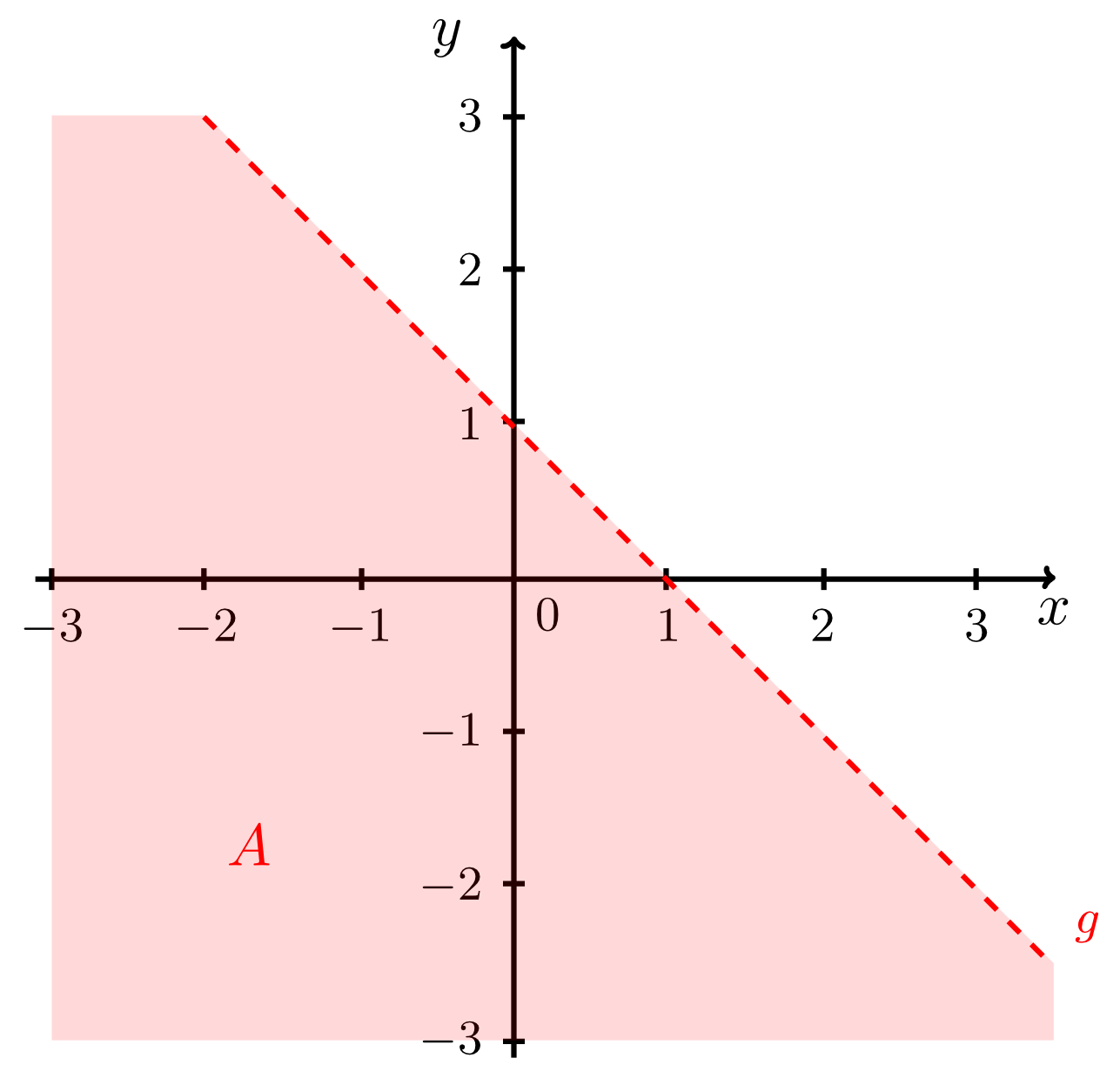
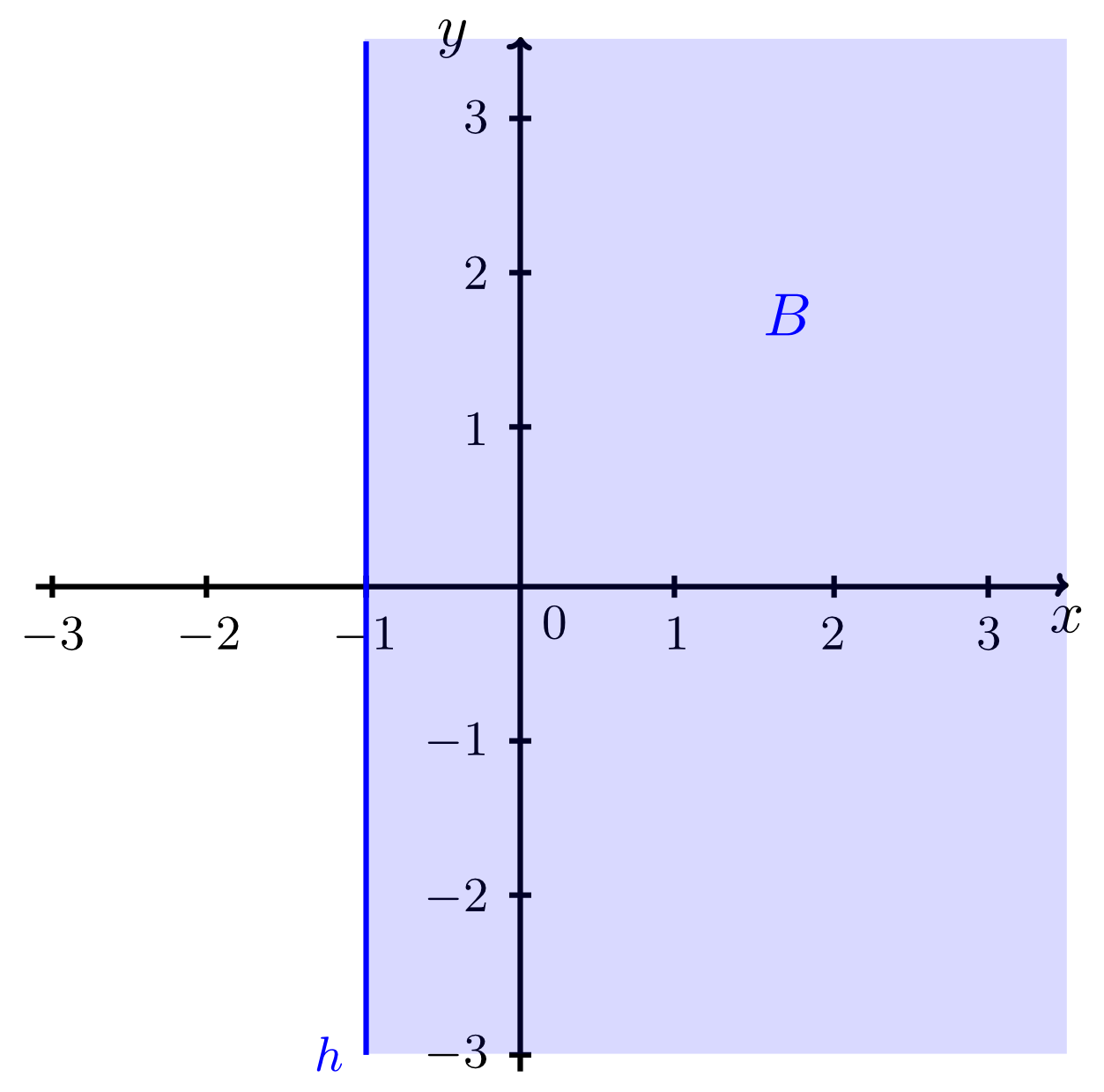
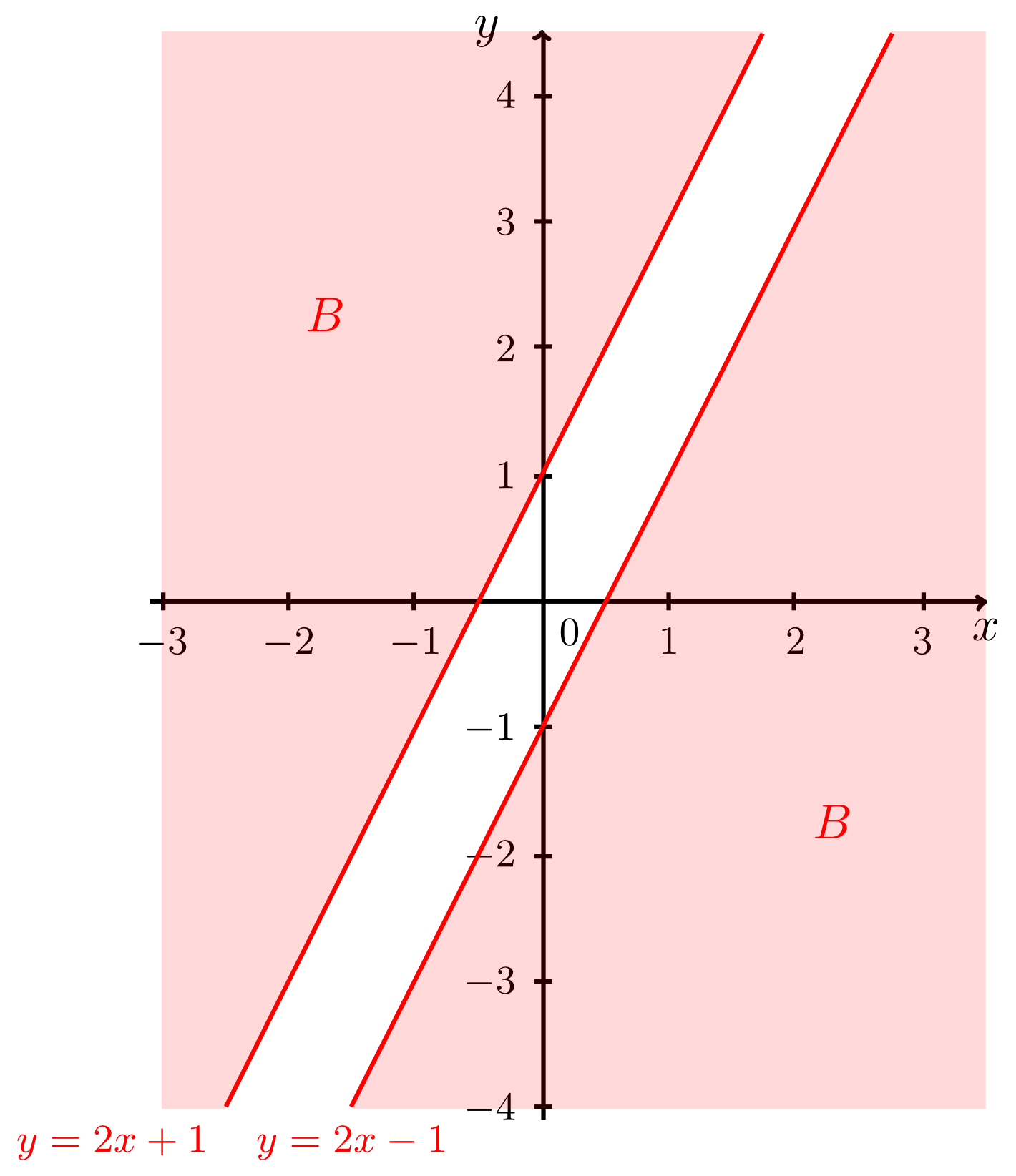
Example 9.4.2
Let two lines be given by the equations
Find and sketch the following sets:
and .
From the Info Box above, we have
and
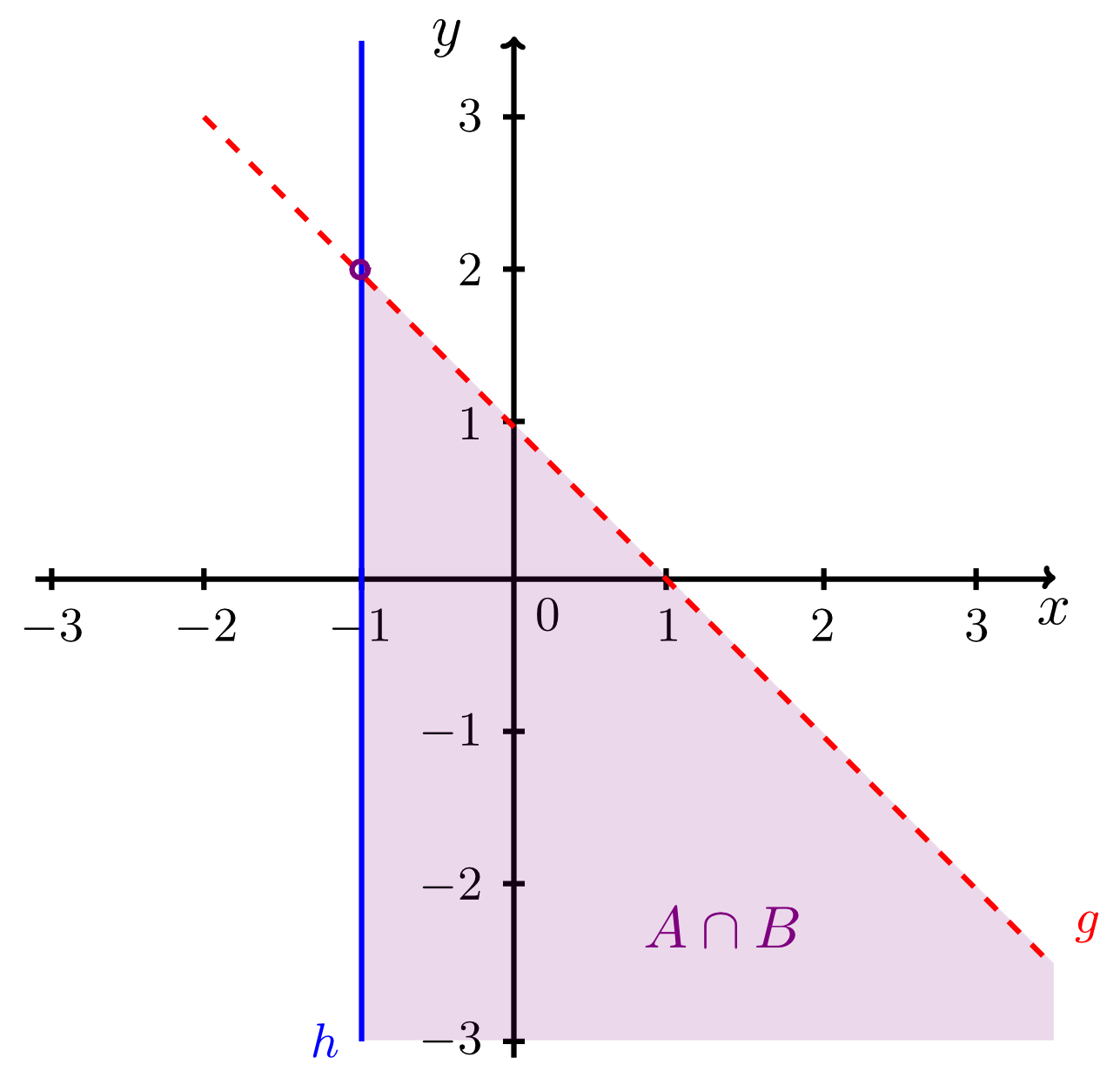
since the points to the right of line have -coordinates that are greater than . Thus, the intersection is the set of points with coordinates that satisfy both the conditions:
This is illustrated by the figures below.
Here, the intersection point of the two lines is not an element of since points on the line are generally excluded from the region . In the figure above this is indicated by a small empty circle at this point.
Find and sketch the following sets:
and .
From the Info Box above, we have
and
since the points to the right of line have -coordinates that are greater than . Thus, the intersection is the set of points with coordinates that satisfy both the conditions:
This is illustrated by the figures below.
Here, the intersection point of the two lines is not an element of since points on the line are generally excluded from the region . In the figure above this is indicated by a small empty circle at this point.
The example above illustrates the following: regions given by coordinate inequalities derived from equations of lines are easy to specify. It becomes more difficult if intersections of such regions are considered. The following, more difficult example shows that even absolute values can be involved.
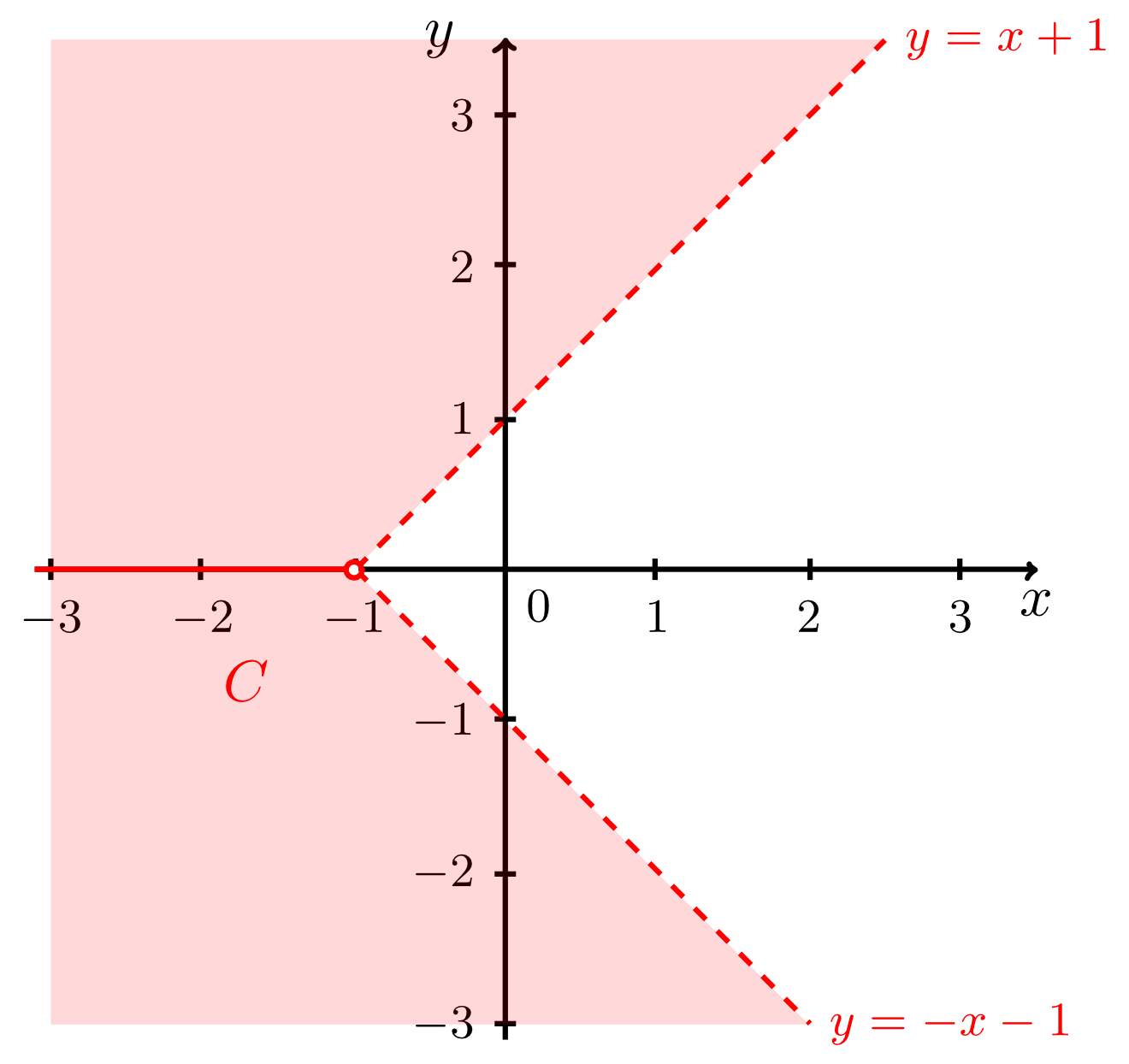
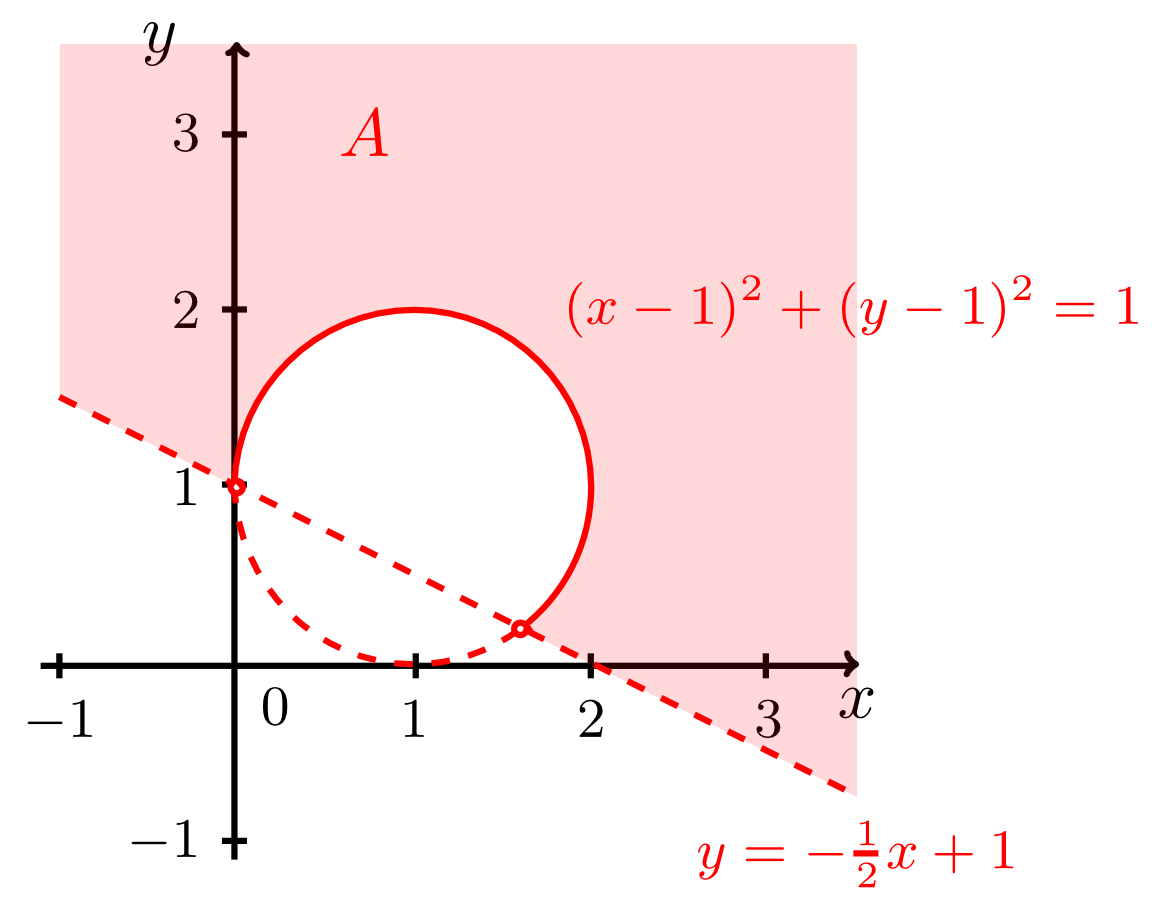
Example 9.4.3
Describe the set defined by
in words and sketch it.
For absolute values (see Section 2.2) a case analysis is required as usual:
The figure below shows the corresponding sketch.
in words and sketch it.
For absolute values (see Section 2.2) a case analysis is required as usual:
-
In this case the inequality can be solved for
Thus, the set contains all points with coordinates that satisfy the inequalities and , i.e. those points that lie above the line but below the angle bisector .
-
In this case the inequality can be solved for
Thus, the set contains all points with coordinates that satisfy the inequalities and , i.e. those points that lie below the line but above the angle bisector .
The figure below shows the corresponding sketch.
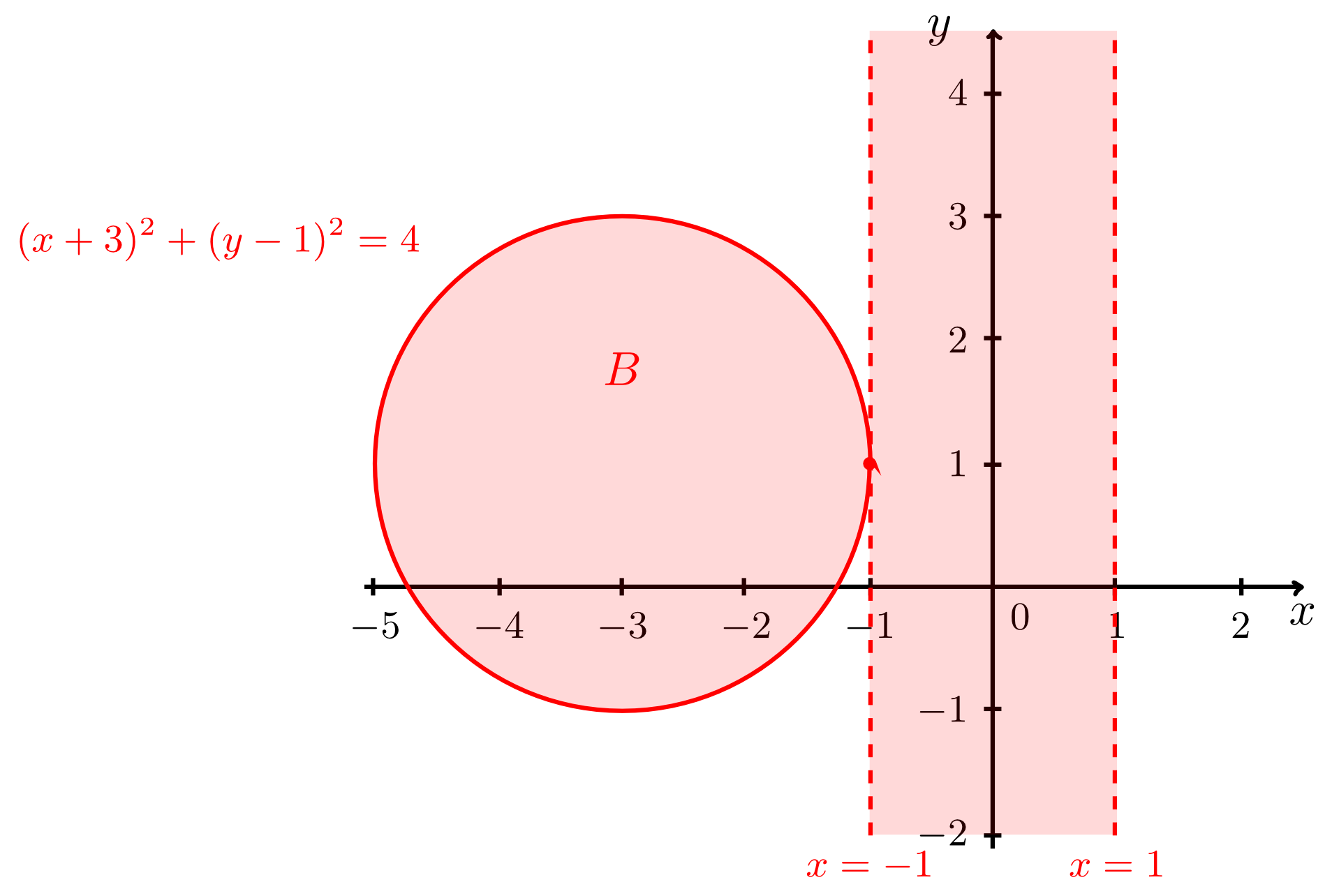
Exercise 9.4.4
Describe and sketch the following sets:
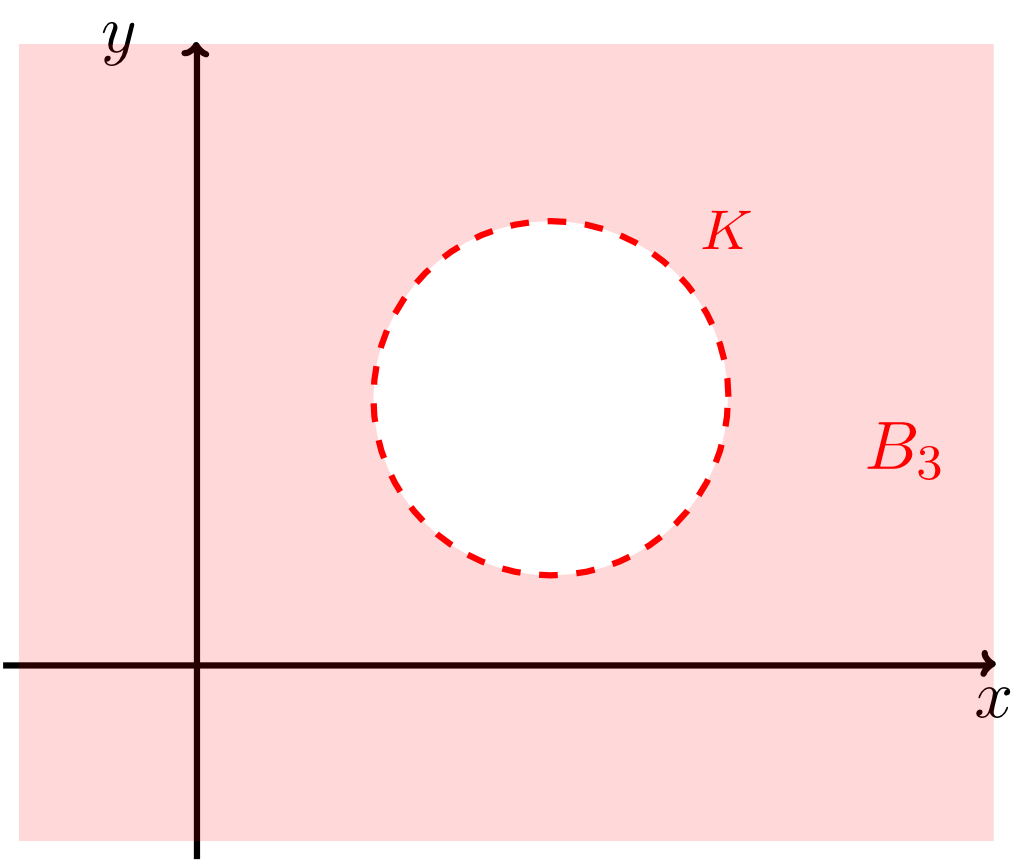
The Info Box below lists the regions in the plane that can be bounded by a circle.
Info 9.4.5
Let a circle in the plane (with the centre and the radius ) be given by the equation
in normal form with respect to a fixed coordinate system. Then replacing the equals sign with an inequality results in the following sets that describe regions an a plane:
- "region within the circle excluding the points on the circle itself"
- "region within the circle including the points on the circle itself"
- "region outside the circle excluding the points on the circle itself"
- "region outside the circle including the points on the circle itself"
The example below shows a few special cases of regions that are bounded by circles as well as a few more complex cases that arise by combining several regions bounded by circles or lines.
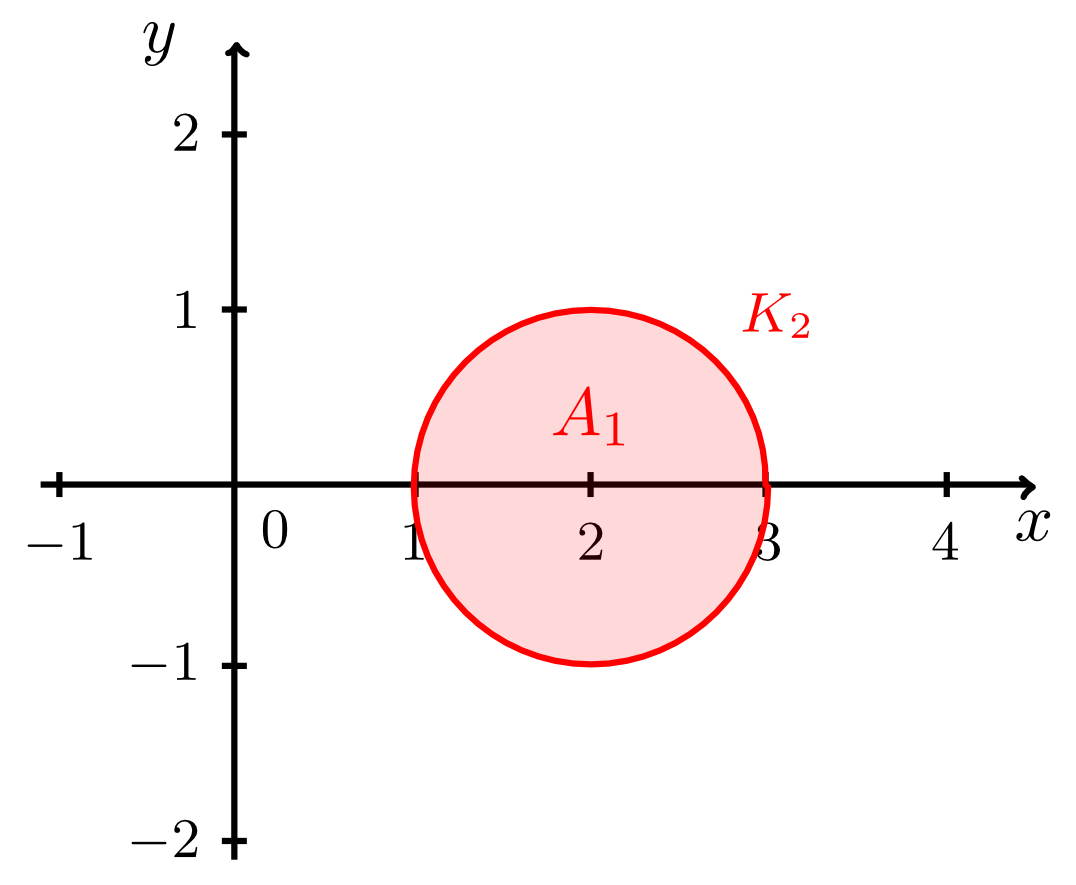
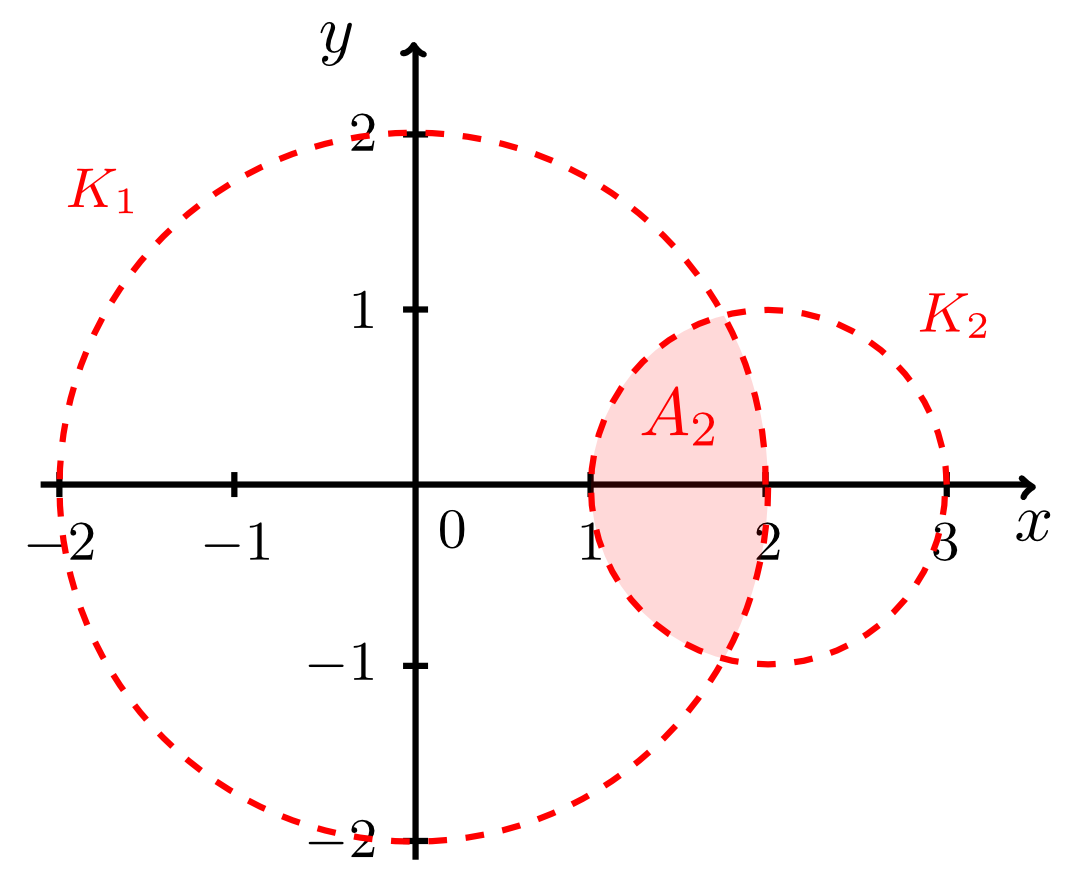
Example 9.4.6
Let two circles and be given by the equations
and
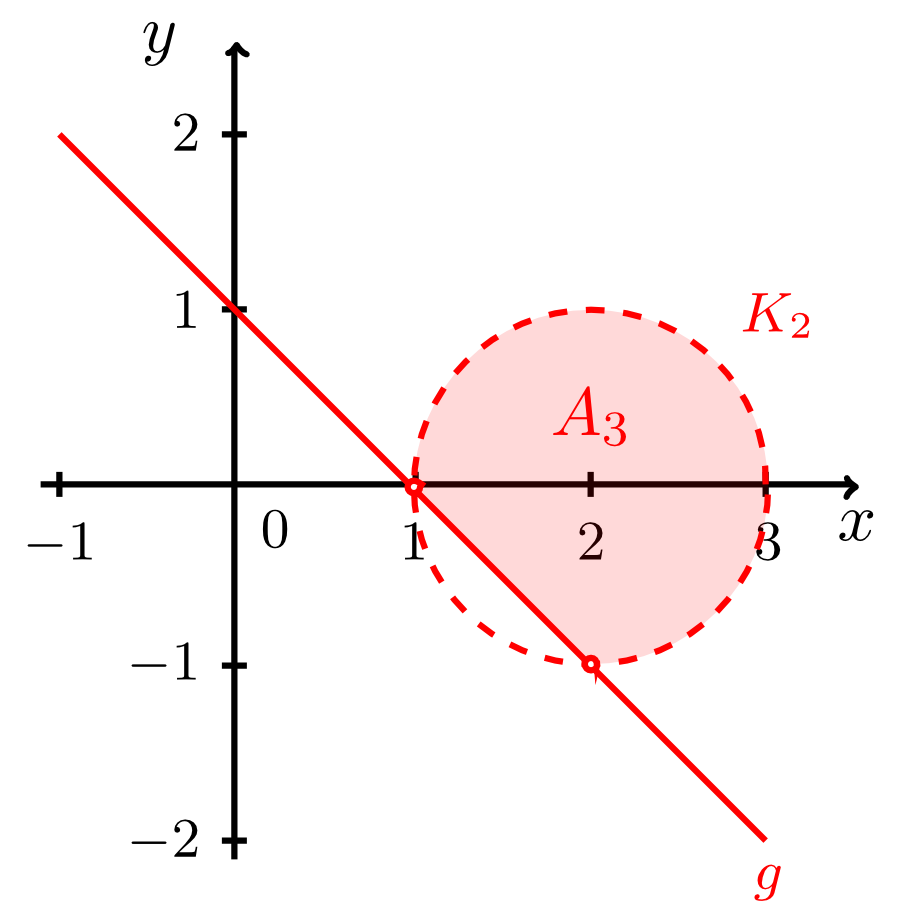
and let the line be given by the equation
and
and let the line be given by the equation
- The set consists of all points within and on the circle :
- The set consists of all points that lie both within the circle and within the circle , i.e. within the intersection of the two discs, excluding the points on the circles themselves:
- The set consists of all points that lie both within the circle - excluding the points on the circle - and above the line :
The intersection points between the circle and the line do not belong to the set .
Exercise 9.4.7
Sketch the given sets:
 Onlinebrückenkurs Mathematik
Onlinebrückenkurs Mathematik