Chapter 9 Objects in the Two-Dimensional Coordinate System

Section 9.3 Circles in the Plane

9.3.3 Coordinate Equations of Circles

With a coordinate system in the plane at hand, we are now able to describe the points on a circle using the term of distance introduced in the previous Section 9.3.2 by an equation, the so-called equation of a circle. In practice, the compulsory root in the equation for the distance is avoided by using the square of the distance. This is allowed since distances are always non-negative. Thus, for two points

P_{1} = (x_{1}; y_{1})

and

P_{2} = (x_{2}; y_{2})

we have:

[\overline{P_{1} P_{2}}] = \sqrt{(x_{2} - x_{1})^{2} + (y_{2} - y_{1})^{2}} \Leftrightarrow [\overline{P_{1} P_{2}}]^{2} = (x_{2} - x_{1})^{2} + (y_{2} - y_{1})^{2} .

This is summarised in the Info Box below.

Info 9.3.4

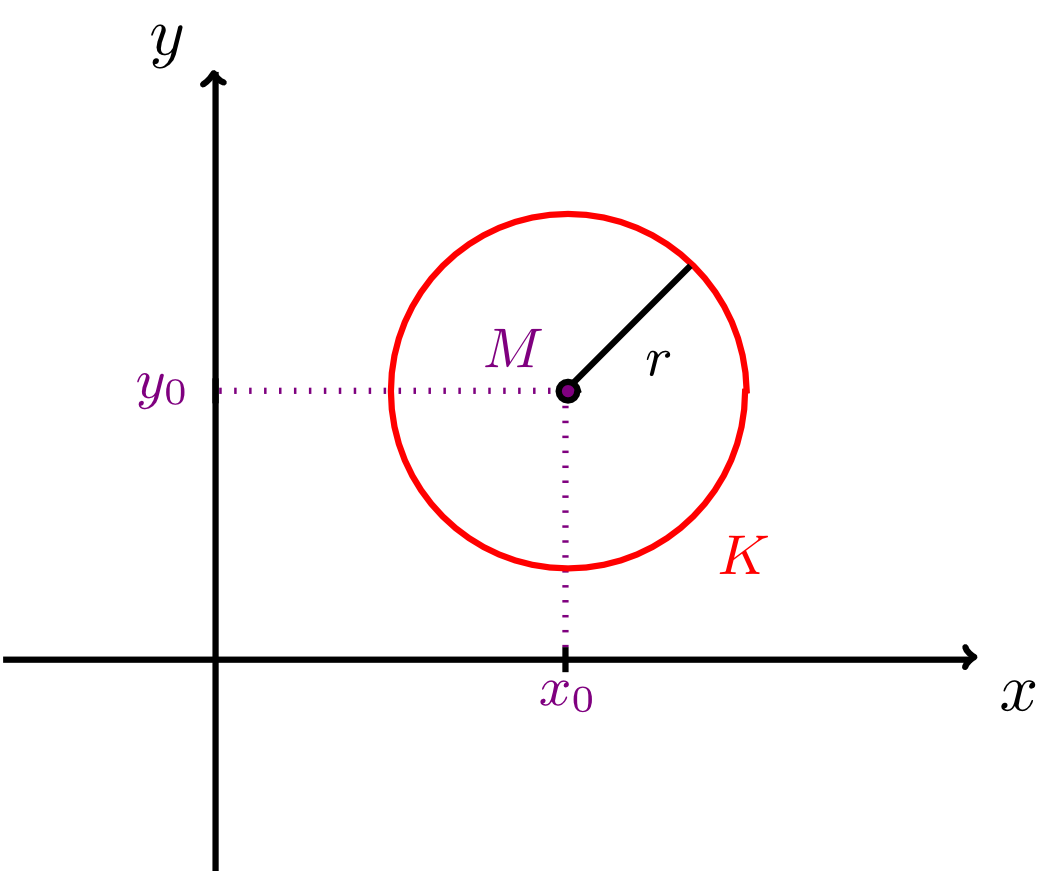
A circle

K

in the plane with a given coordinate system is the set of all points that have a fixed distance

r > 0

, the radius, from a common centre

M = (x_{0}; y_{0})

. By specifying the radius and the centre a circle is uniquely defined. Thus, we have:

K = {(x; y) \in ℝ^{2} : (x - x_{0})^{2} + (y - y_{0})^{2} = r^{2}} .

As for lines, often just the equation of a circle is given:

K : (x - x_{0})^{2} + (y - y_{0})^{2} = r^{2} .

All points with coordinates that satisfy the equation of a given circle belong to the circle. This is illustrated by the figure below.

Using the equation of a circle we are now able to describe arbitrary circles in the plane as well as points that lie on that circle and points that do not.

Example 9.3.5

The circle with centre

P = (2; 1)

and radius

r = 2

is described by the following equation:

(x - 2)^{2} + (y - 1)^{2} = 2^{2} = 4 .

Thus, all points that have the distance of

2

from the point

P

lie on the circle. For example, the point

Q = (0; 1)

lies on the circle since we have

(0 - 2)^{2} + (1 - 1)^{2} = (- 2)^{2} + 0^{2} = 4 .

In contrast, the point

R = (3; - 2)

does not lie on the circle since its distance from the point

P

[\overline{P R}] = \sqrt{(2 - 3)^{2} + (1 - (- 2 {))}^{2}} = \sqrt{10} \neq 2 .

The coordinates of the point

R

do not satisfy the given equation of a circle.

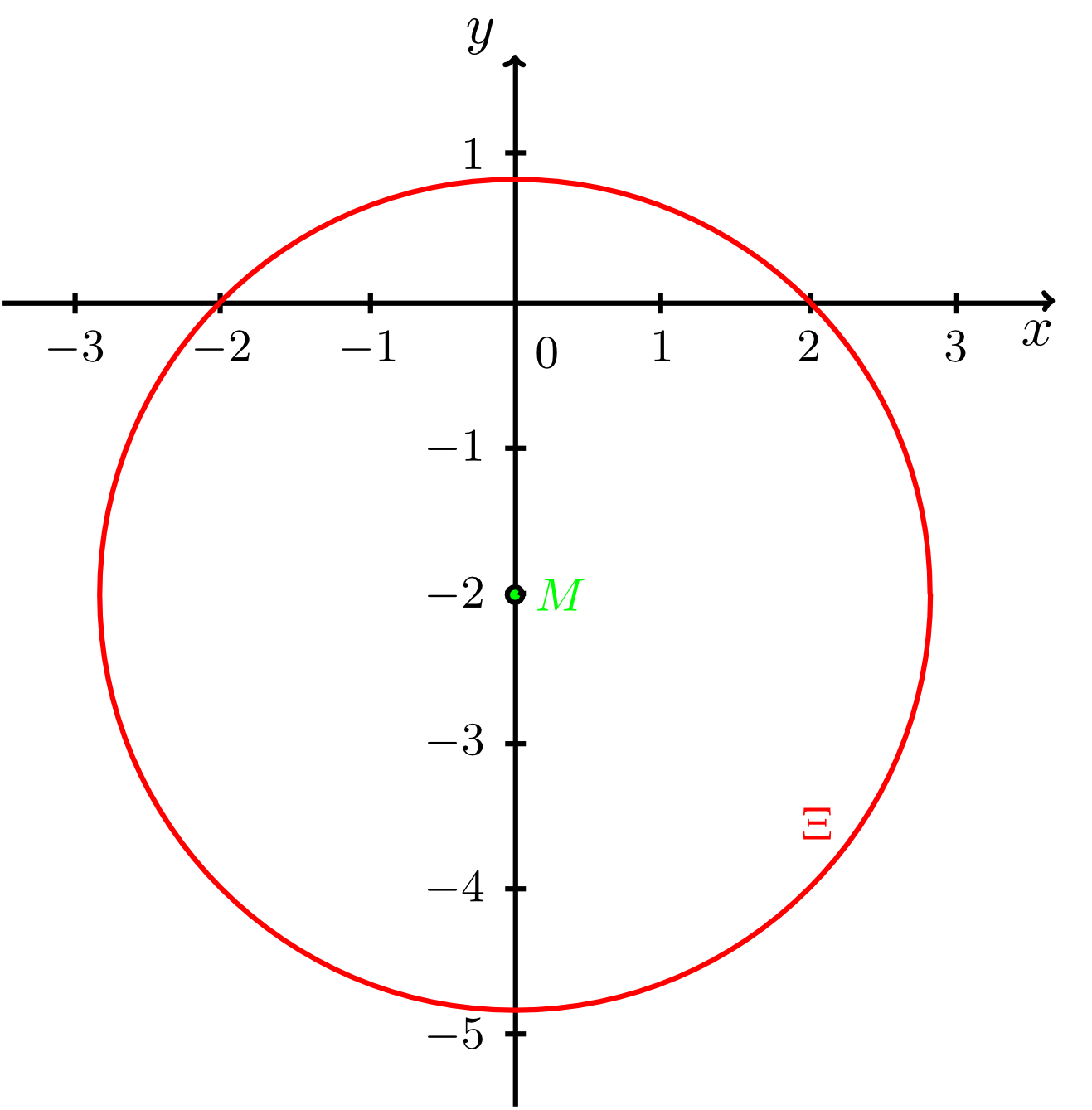
An important special case is any circle that has the origin of the coordinate system as its centre. For example, the equation

x^{2} + y^{2} = 2

describes a circle with a radius of

\sqrt{2}

centred at the origin

(0; 0)

(see figure below).

The most special case of this is the circle with a radius of

1

at the origin

(0; 0)

This circle is called the unit circle, and it is important in trigonometry (see Section 5.6 and Section 6.5).

Exercise 9.3.6

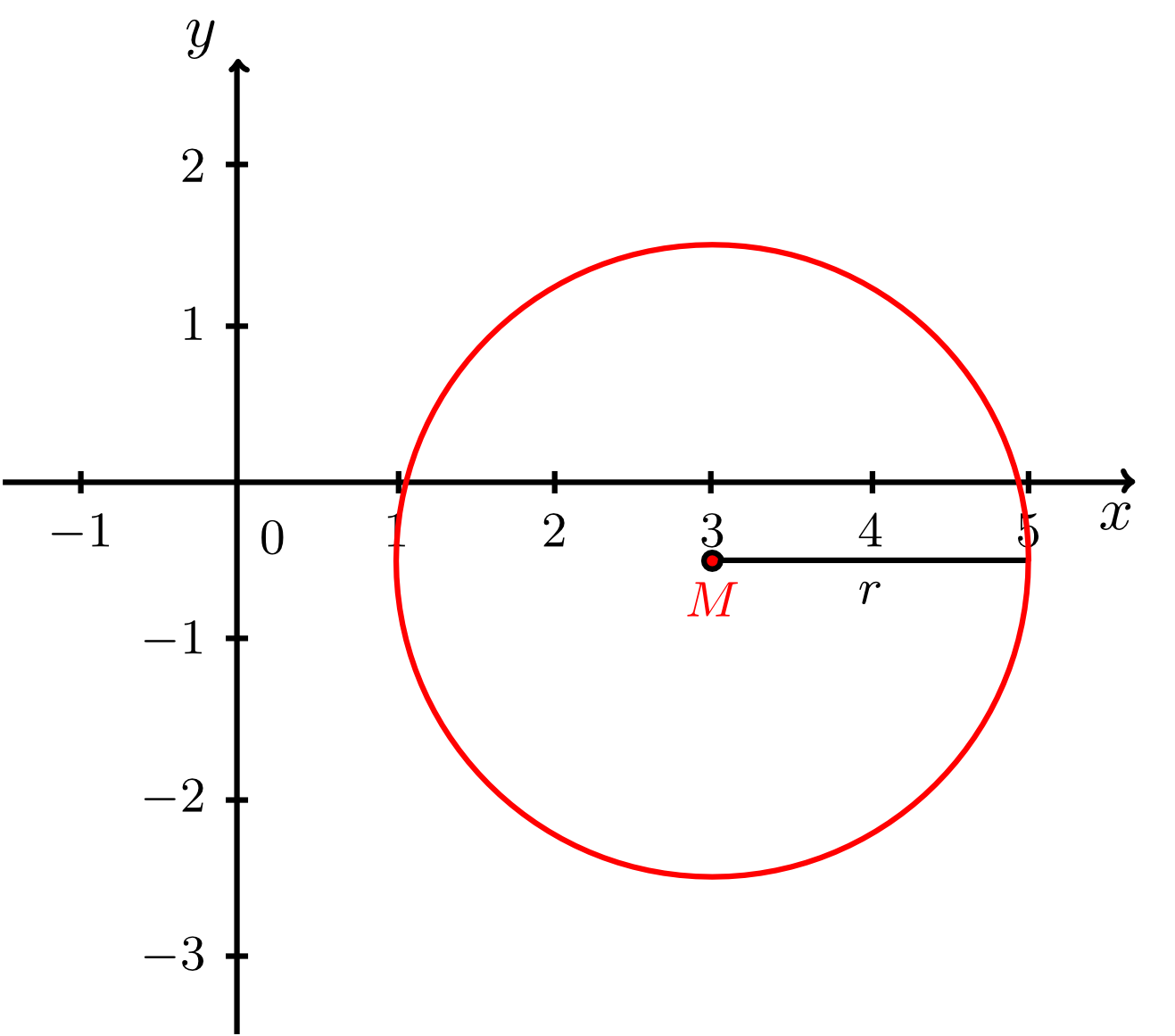
Let a circle $Ξ$ be given by the equation

$Ξ : x^{2} + (y + 2)^{2} = 8 .$
Its centre is at $M =$
and its radius is $r =$
. Draw the circle.
The equation of a circle with a radius of $1$ at $(- 2; - 1)$ is

$= 1$ .
Decide whether the given points lie on the circle. Tick those points that lie on the circle.

The origin

$(1; 1)$

$(- 2; 0)$

$(- \frac{3}{2}; \frac{\sqrt{3} - 2}{2})$

$M = (0; - 2)$

$r = 2 \sqrt{2}$
$(x + 2)^{2} + (y + 1)^{2} = 1$
The origin and the point $(1; 1)$ do not lie on the circle but the points $(- 2; 0)$ and $(- \frac{3}{2}; \frac{\sqrt{3} - 2}{2})$ do, as can be seen by substituting the coordinates of the points into the given equation of a circle:

$(0 + 2)^{2} + (0 + 1)^{2} = 4 + 1 = 5 \neq 1,$

$(1 + 2)^{2} + (1 + 1)^{2} = 9 + 4 = 13 \neq 1,$

$(- 2 + 2)^{2} + (0 + 1)^{2} = 0 + 1 = 1,$

${(- \frac{3}{2} + 2)}^{2} + {(\frac{\sqrt{3} - 2}{2} + 1)}^{2} = {(\frac{1}{2})}^{2} + {(\frac{\sqrt{3}}{2})}^{2} = \frac{1}{4} + \frac{3}{4} = 1 .$

As the examples and exercises above show, it is rather easy to read off the centre and the radius of the circle from its equation of a circle if it is given in the form

(x - x_{0})^{2} + (y - y_{0})^{2} = r^{2}

described in Info Box 9.3.4. Therefore, this form is also called normal form. Unfortunately, the equation of a circle is often not given in this simple form but has to be transformed by a few calculation steps to enable us to read off the the centre and the radius. This approach is illustrated in the example below.

Example 9.3.7

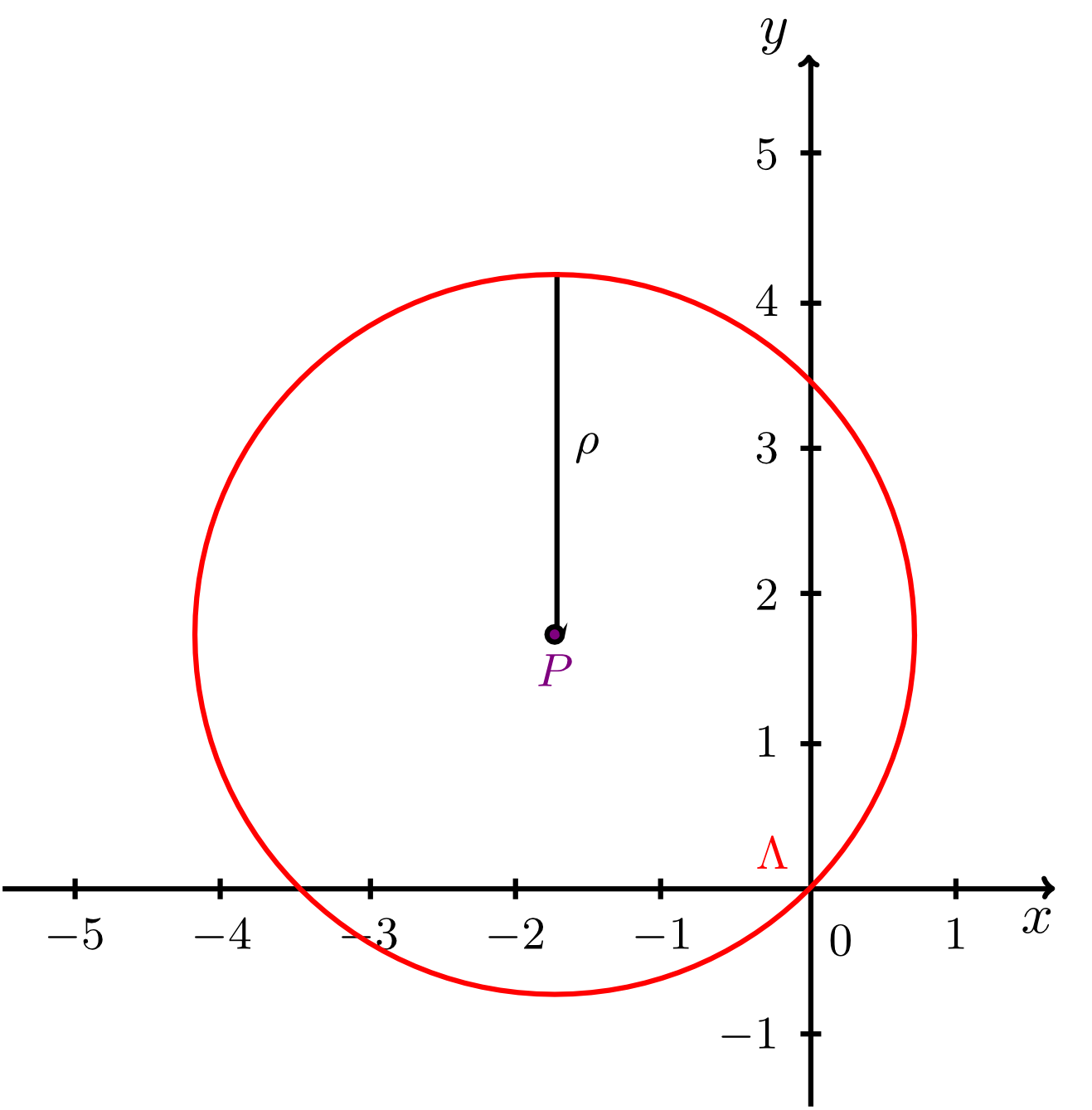
Let a circle

K

be given by the equation

K : x^{2} + y^{2} - 6 x + y + \frac{21}{4} = 0 .

You can neither immediately see that this is an equation of a circle nor read off the centre and the radius. This equation can be transformed into normal form using the method of completing the square. We will apply this method separately to the terms containing

x

and the terms containing

y

in the equation of a circle given above.
For the terms containing

x

, we have

x^{2} - 6 x = x^{2} - 2 \cdot 3 x = x^{2} - 2 \cdot 3 x + 3^{2} - 3^{2} = x^{2} - 6 x + 9 - 9 = (x - 3)^{2} - 9,

and for the terms containing

y

, we have

y^{2} + y = y^{2} + 2 \cdot \frac{1}{2} y = y^{2} + 2 \cdot \frac{1}{2} y + {(\frac{1}{2})}^{2} - {(\frac{1}{2})}^{2} = y^{2} + y + \frac{1}{4} - \frac{1}{4} = {(y + \frac{1}{2})}^{2} - \frac{1}{4} .

For the equation of the circle, this implies:

x^{2} + y^{2} - 6 x + y + \frac{21}{4} = 0 \Leftrightarrow (x - 3)^{2} - 9 + {(y + \frac{1}{2})}^{2} - \frac{1}{4} + \frac{21}{4} = 0 \Leftrightarrow (x - 3)^{2} + {(y + \frac{1}{2})}^{2} = 4

This is the normal form of the equation of this circle, and we can read off the centre

M = (3; - \frac{1}{2})

and the radius

r = 2

easily (see figure below).

Exercise 9.3.8

Find the centre

P

and the radius

ρ

of the circle

Λ = {(x; y) : x^{2} + 2 \sqrt{3} x = 2 \sqrt{3} y - y^{2}} .

Transform the equation of the circle into normal form using the method of completing the square. In addition, sketch the circle.

P =

ρ =

x^{2} + 2 \sqrt{3} x = 2 \sqrt{3} y - y^{2} \Leftrightarrow x^{2} + 2 \sqrt{3} x + y^{2} - 2 \sqrt{3} y = 0 \Leftrightarrow x^{2} + 2 \sqrt{3} x + 3 + y^{2} - 2 \sqrt{3} y + 3 = 6

\Leftrightarrow (x + \sqrt{3})^{2} + (y - \sqrt{3})^{2} = 6

Thus, we have

P = (- \sqrt{3}; \sqrt{3})

and

ρ = \sqrt{6}

Onlinebrückenkurs Mathematik

1. Elementary Arithmetic

2. Equations in one Variable

3. Inequalities in one Variable

4. System of Linear Equations

5. Geometry

6. Elementary Functions

7. Differential Calculus

8. Integral Calculus

9. Objects in the Two-Dimensional Coordinate System

10. Basic Concepts of Descriptive Vector Geometry

11. Language of Descriptive Statistics