Chapter 5 Geometry

Section 5.1 Elements of Plane Geometry

5.1.2 Points and Lines

In geometry, a place or a position in a plane is idealised to the most basic object, namely a point. A single point itself cannot be characterised any further.
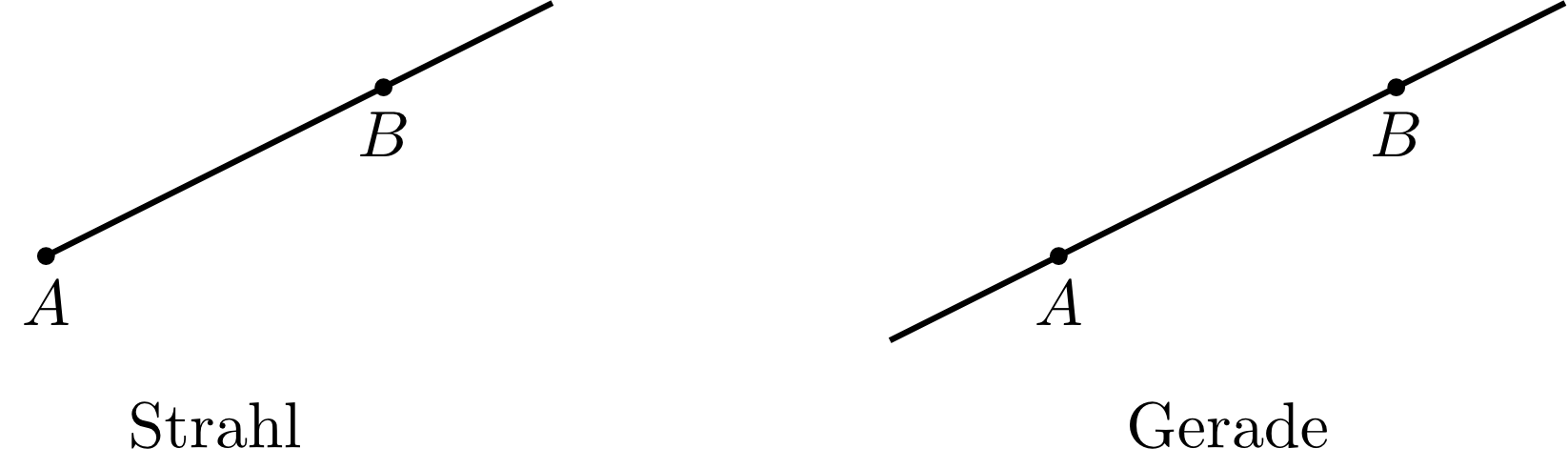
For several points, relations between these points can be considered in different ways - and points can be used to define new objects such as line segments and lines (see figure below). Mathematically, these objects are sets of points.

First, we consider a line segment and the distance between points. To do this, we need a comparison tool for measuring distance. In mathematics, this tool is a comparative length called the unit length. For applications, appropriate length units such as metres or centimetres are chosen, depending on the task in hand.

A ray of light emitted by a distant star or by the sun is an appropriate notion of a ray starting at the initial point $A$ and proceeding through a second point $B$ indefinitely. A ray is also called a half-line.

Continuing the path of a line segment $\overline{AB}$ on both ends indefinitely results in a line.

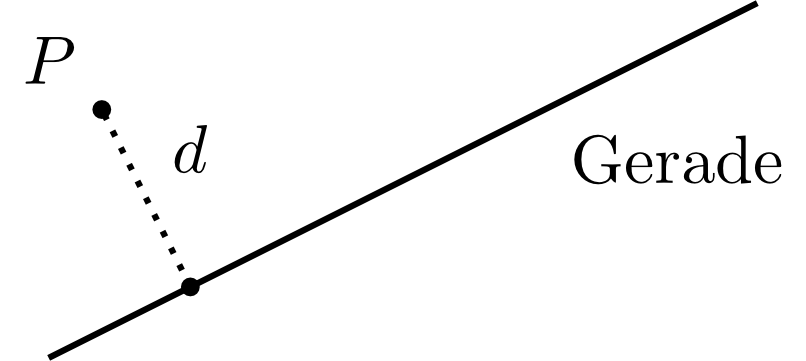
Considering, beside $A$ and $B$, an additional point $P$, we can ask for the distance $d$ of the point $P$ from the line $AB$, which is defined as the shortest path between $P$ and one of the points of the line $AB$.

Given three points $P$, $Q$, and $S$ in the plane, the lines $SP$ and $SQ$ can be defined.
The two lines have the point $S$ in common. If the point $Q$ is also on the line $SP$, then $SQ$ and $SP$ denote one and the same line. If the point $Q$ does not belong to the line $SP$, the line $SQ$ is different from the line $SP$. Then, the two lines have only the point $S$ in common. The point $S$ is called an intersection point.
If any two lines $g$ and $h$ do not have any points in common, the smallest distance between points on $g$ and $h$, respectively, is called the distance between the lines $g$ and $h$. Hence, $g$ and $h$ do not have any point in common if they have a distance larger than $0$. Two lines are called parallel if every point on one of the two lines has the same distance from the other line.
A single line can be described by the distance of two points $M$ and $M\text{'}$ as well: The set of all points with the same distance from two points $M$ and $M\text{'}$ is a line.
In geometry, it is a typical approach to define new objects by means of certain properties such as the distance. In this way, a circle can also be described very easily.