Chapter 5 Geometry

Section 5.4 Polygons, Area and Circumference

5.4.2 Quadrilaterals


In the previous section 5.3, triangles were considered. They were defined by three non-collinear points. Connecting any two of the three points by a line segment always results in a single closed path in which every point connects exactly two line segments. The line segments in the path have only their endpoints in common. Furthermore, the line segments do not intersect.
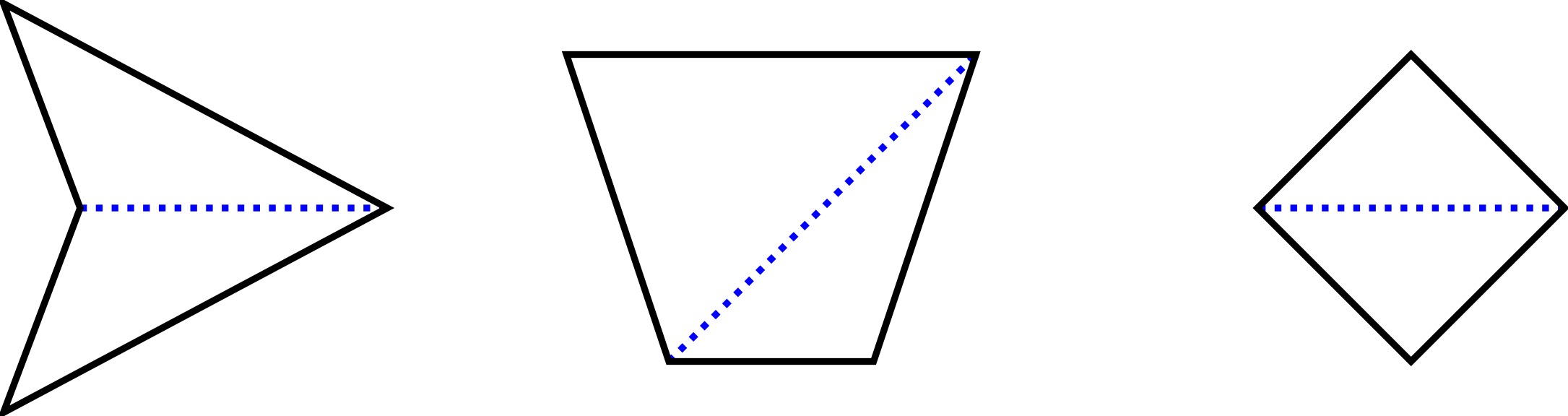
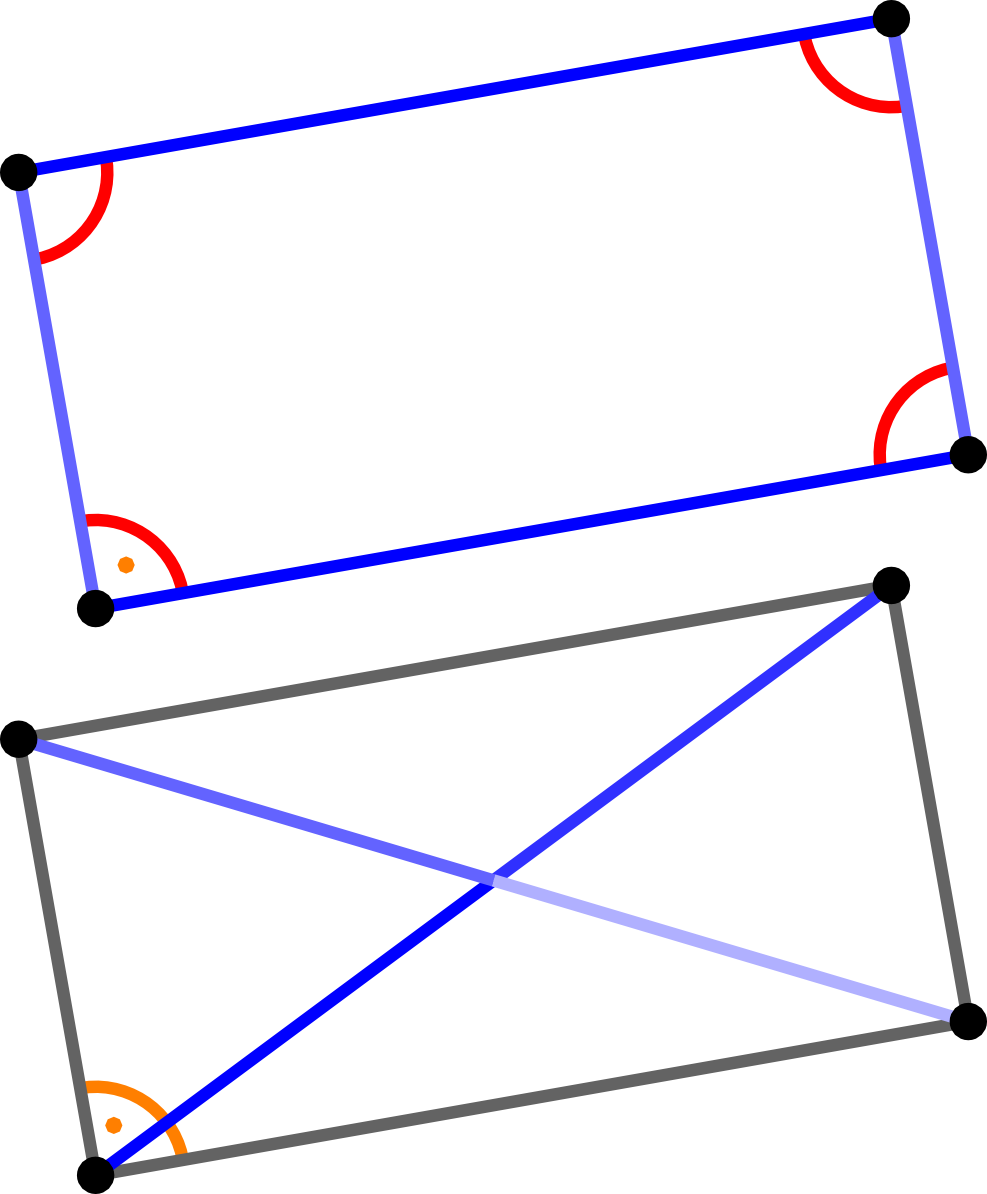
For more than three points this is not always true. Even only four points can be connected in such a way that line segments intersect or more than one closed path exists.
In the figure below all given points are to be connected by a single closed path without any intersections.

Obviously, a quadrilateral can be divided into two triangles. Generally, one obtains two triangles if the vertex with the greatest angle is connected to the opposite vertex by a line segment. Such an additional line segment between two vertices of the quadrilateral which are not connected to each other is called a diagonal of the quadrilateral. From the fact that the sum of (interior) angles in a triangle equals π or 180 ∘ then results that the sum of (interior) angles in a quadrilateral is twice this sum, i.e. 2π or 360 ∘ .
Quadrilaterals 5.4.1

Consider quadrilaterals constructed by connecting the four given points by line segments forming a single, closed and non-intersecting path trough these four points. There, any three of the four points connected by two line segments must be non-collinear.
As for triangles, the interior angles of quadrilaterals are simply denoted as angles if not otherwise specified in context.

Like triangles, quadrilaterals are used in technical structures in many ways. Therefore, additional terms are commonly used to specify different types of quadrilaterals.
Also as for triangles, quadrilaterals are classified by the lengths of their sides or by the magnitudes of angles. There are differences between the classifications of triangles and quadrilaterals. For example, quadrilaterals can have parallel sides, or have more than one vertex with a right angle.
Special Types of Quadrilaterals 5.4.2

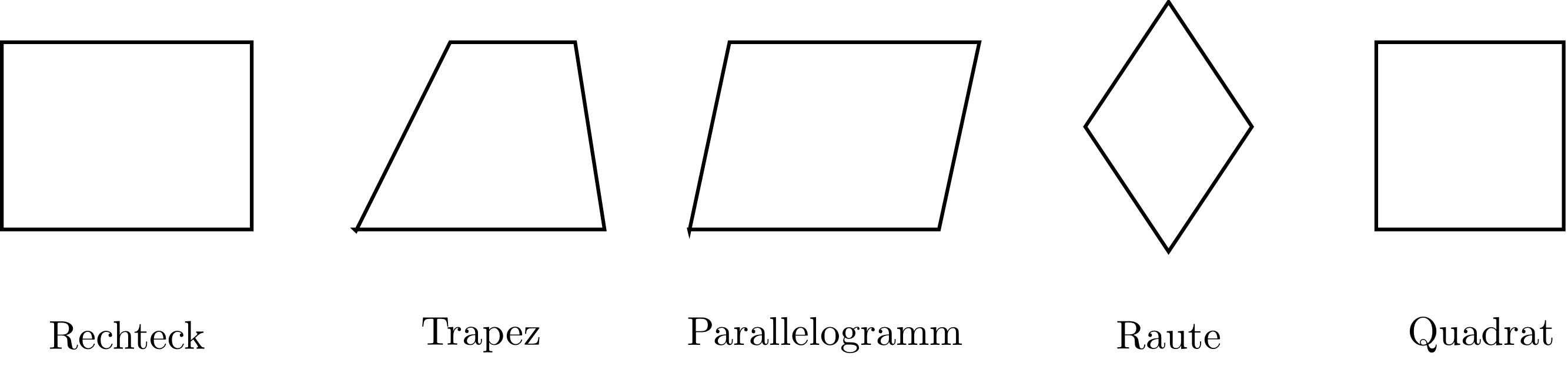
Quadrilaterals with the following properties have their own terms: A quadrilateral is called
  • a trapezoid if at least one pair of opposite sides is parallel;
  • a parallelogram if two pairs of opposite sides are parallel;
  • a rhombus or an equilateral quadrilateral or a diamond if all four sides are of equal length;
  • a rectangle if all four (interior) angles are right angles;
  • a square if it is a rectangle with four sides of equal length;
  • a unit square if it is a square with sides of length 1.

Thus, for the unit square also a measure has to be fixed.

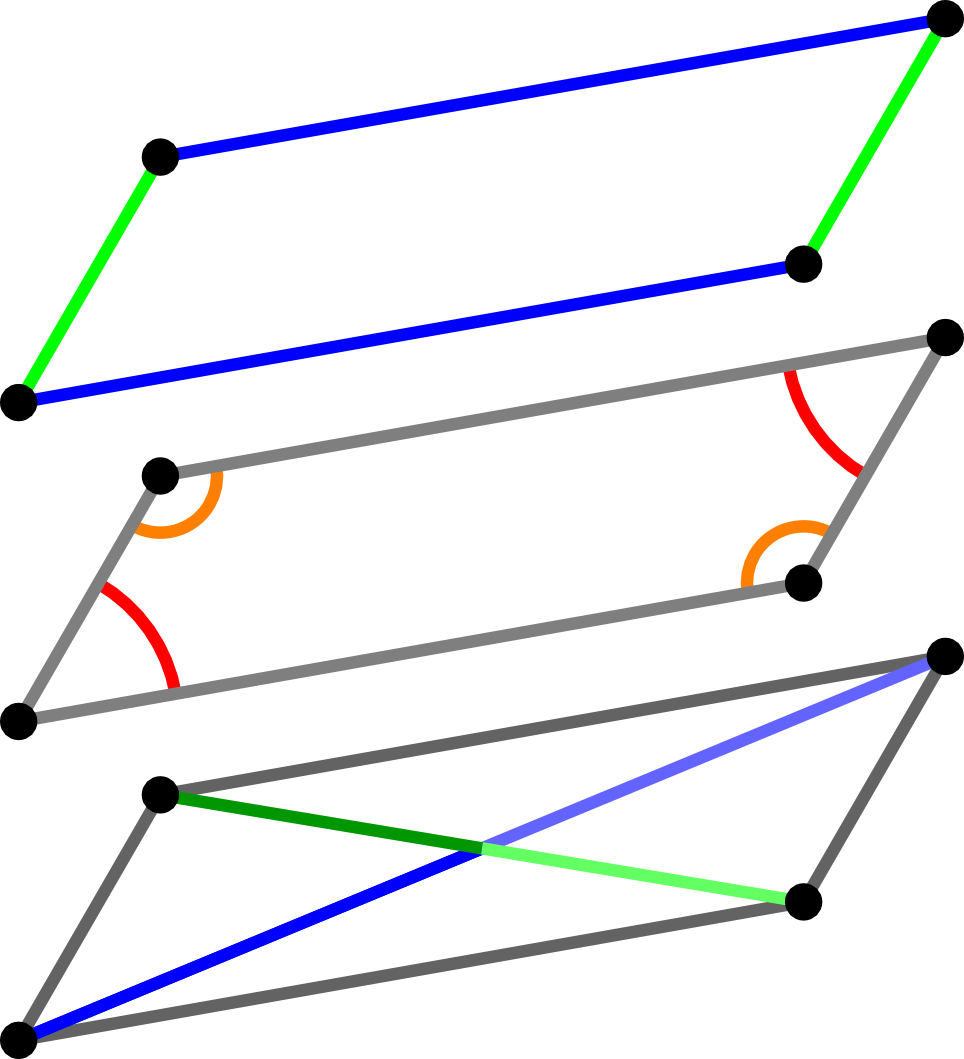
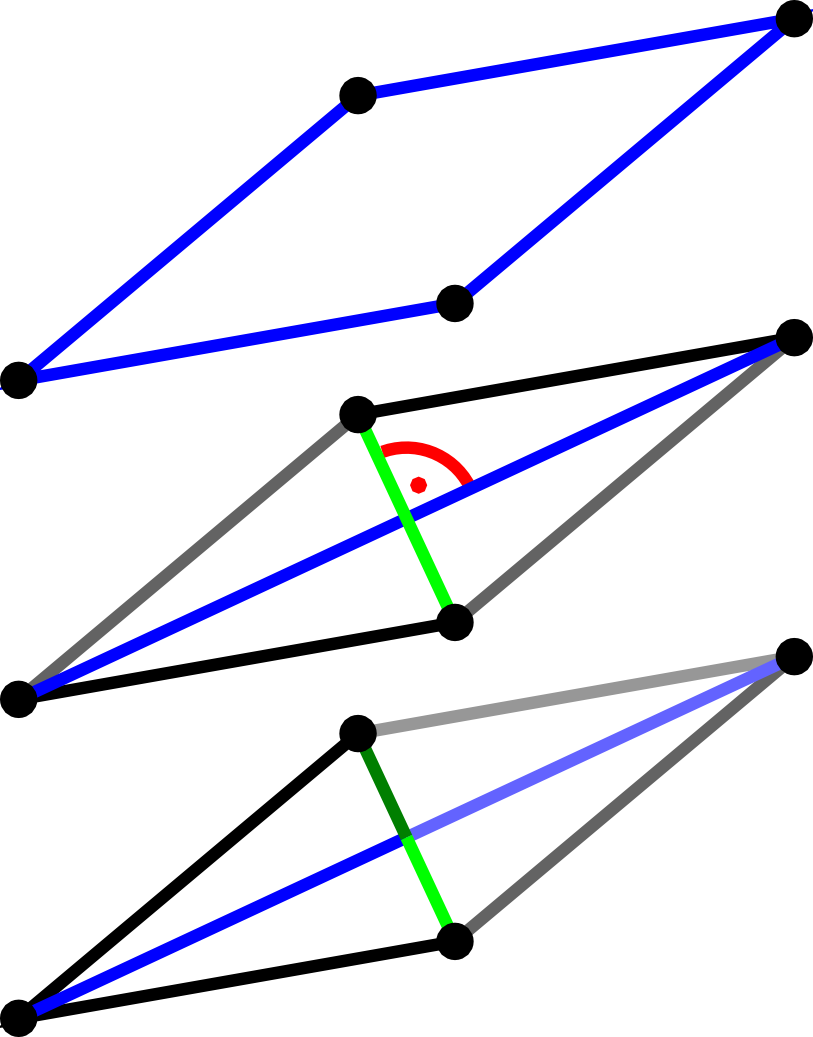
There are several relations between the quadrilaterals introduced above:
Relations between rectangles 5.4.3
Between different quadrilaterals the following relations exist:
  • Every square is a rectangle.
  • Every square is a rhombus.
  • Every rhombus is a parallelogram.
  • Every rectangle is a parallelogram.
  • Every parallelogram is a trapezoid.

These quadrilaterals can be characterised by means of the properties of their sides, angles, or diagonals in many ways.
Parallelogram 5.4.4

A quadrilateral is a parallelogram if and only if
  • opposite sides are parallel;
  • opposite sides are of equal length;
  • opposite (interior) angles are equal;
  • two adjacent (interior) angles sum up to π or 180 ∘ , respectively;
  • diagonals bisect each other.


Rhombuses can be described as a special type of parallelograms.
Rhombus 5.4.5


A quadrilateral is a rhombus if and only if
  • all sides are of equal length;
  • it is a parallelogram in which the diagonals are perpendicular;
  • at least two adjacent sides are of equal length and the diagonals bisect each other.


In the case of rectangles one often thinks of right angles since the term rectangle comes from the Latin word rectangulus, which is a combination of rectus (right) and angulus (angle). Apart from that, rectangles can simply be described by means of the properties of their diagonals.
Rectangle 5.4.6

A quadrilateral is a rectangle if and only if
  • all (interior) angles are equal;
  • it is a parallelogram containing at least one right angle;
  • it is a parallelogram whose diagonals are of equal length;
  • the diagonals are of equal length and bisect each other;
  • the diagonals bisect each other and at least one (interior) angle is a right angle.


Squares are both special types of rectangles and special types of rhombuses.
Square 5.4.7


A quadrilateral is a square if and only if
  • all sides are of equal length and
    • all (interior) angles are equal or
    • at least one (interior) angle is a right angle;

  • the diagonals are of equal length and in addition all sides are of equal length;
  • the diagonals are perpendicular and
    • bisect each other and are of equal length or
    • all (interior) angles are equal;

  • it is a rhombus whose diagonals are of equal length;
  • it is both a rhombus and a rectangle.


: