Chapter 5 Geometry

Section 5.3 All about Triangles

5.3.4 Congruence and Similar Triangles


Each triangle includes three sides and three angles. The exterior angles are already defined by the interior angles such that the "shape" of a triangle is determined by six characteristics. If two triangles coincide in all these characteristics, they are said to be congruent. For that, the position of the triangles is not relevant, i.e. congruent triangles can be transformed into each other by rotation, reflection, and translation.
If four of the six characteristics are known, the triangle is uniquely determined up to rotation or reflection, i.e. its position in the plane. Then, all triangles with these characteristics are congruent. In some cases, only three characteristics are sufficient to determine the triangle uniquely. These cases are described by the following theorems for congruent triangles.
Theorems for Congruent Triangles 5.3.13

Up to its position in the plane, a triangle is uniquely defined if one of the following situations is at hand:
  • At least four of the six characteristics (three angles and three sides) are known.
  • The lengths of all three sides are known.
    (This theorem is usually called "sss" for "side, side, side".)
  • Two angles and the length of the included side are known.
    (This theorem is usually called "asa" for "angle, side, angle".)
  • The lengths of two sides and the included angle are known.
    (This theorem is usually called "sas" for "side, angle, side".)
  • The lengths of two sides and a non-included angle are known such that only one side is a leg of the given angle and the second side is greater than the given leg.
    (This theorem is called "Ssa", where the upper-case "S" indicates that the side opposite to the given angle is the greater one.)

If only two characteristics of a triangle are known, or three characteristics are known that do not correspond to one of the cases described above, than a number of different triangles with these characteristics exist which are not congruent.
The next example will illustrate how a triangle can be constructed applying the theorems for congruent triangles. Then another example will be considered, where only three angles are known and hence none of the theorems described above apply.
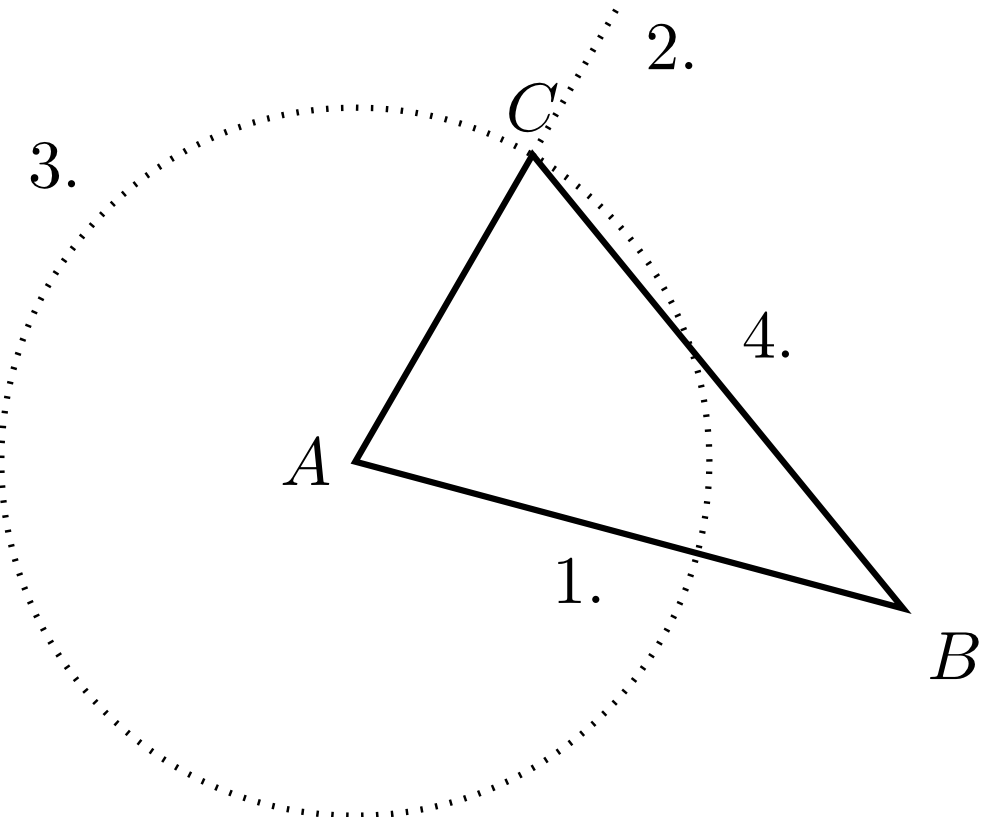
Example 5.3.14

Let the sides b, c, and the angle  α be given. According to the "sas" theorem the triangle is constructed as follows: 1. Draw a line, in this example side c. 2. Attach the angle α to the corresponding vertex ( A). 3. Draw a circle around vertex A with a radius corresponding to the length of the second side (in this case, side b). 4. The intersection point of this circle with the second leg of the angle  α is the third vertex ( C) of the triangle. (The first leg of α is the side c.)


Exercise 5.3.15
Construct a triangle with side c=5 and the two angles α=30 ∘ and β=120 ∘ using the notation introduced above.

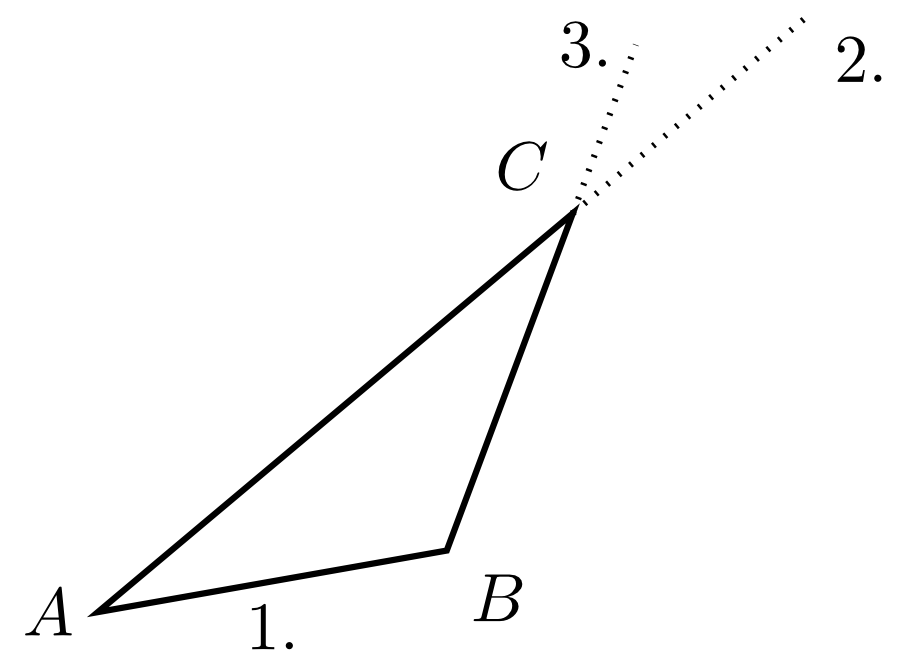
Example 5.3.16
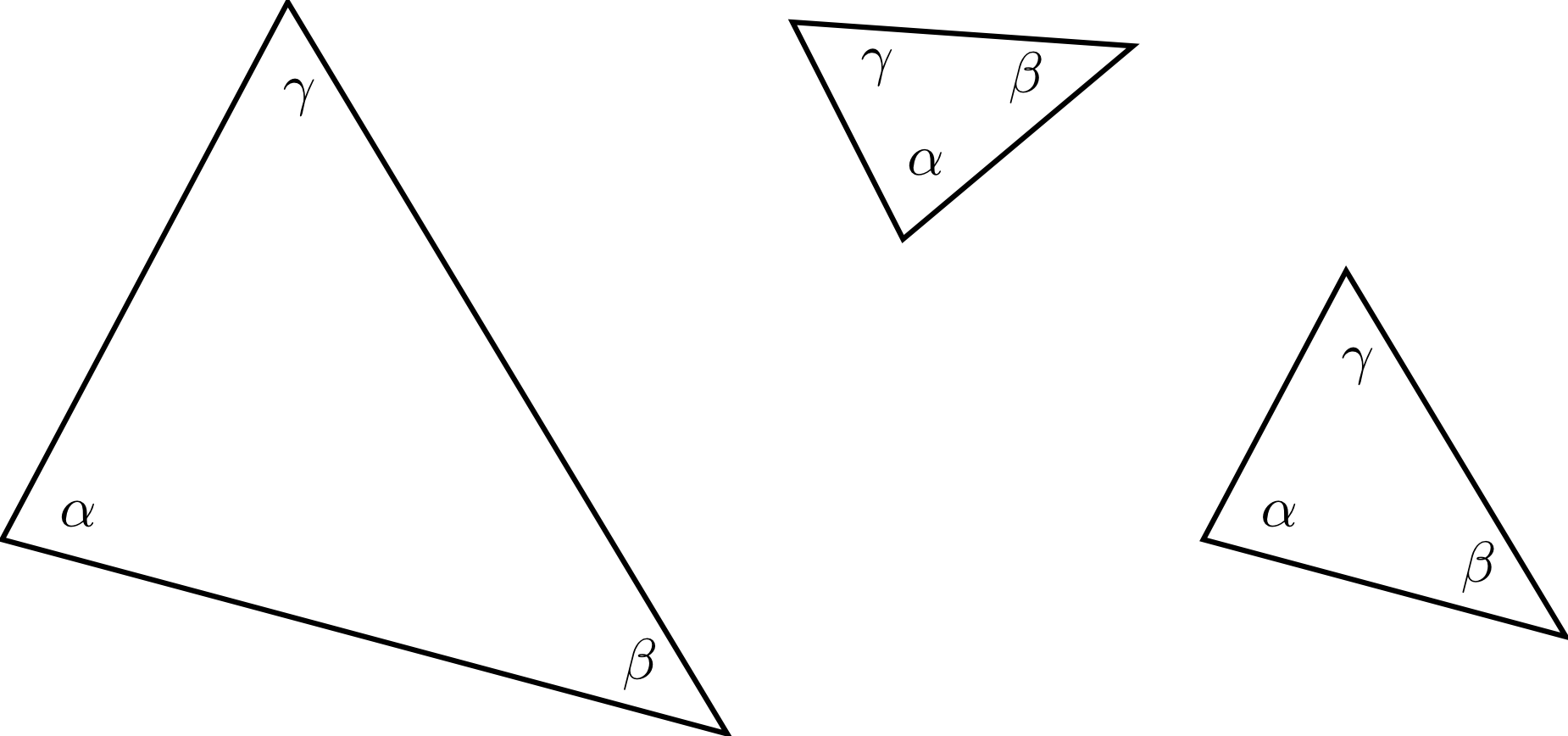
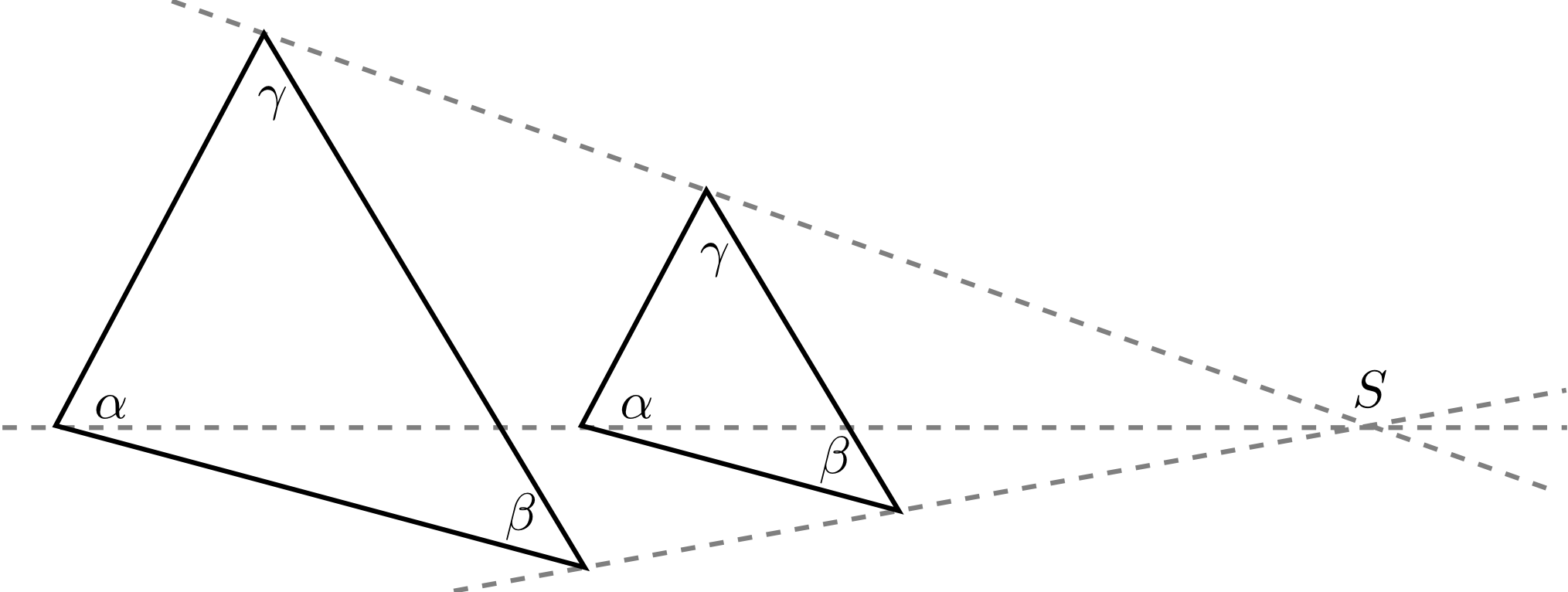
Let three angles α=77 ∘ , β=44 ∘ , and γ=59 ∘ be given summing up to 180 ∘ . This case does not correspond to one of the cases in the theorems for congruent triangles 5.3.13. A few examples for triangles with the given angles are shown below.

Actually, an infinite number of triangles with the given angles do exist. They are not congruent to each other, i.e. they cannot be transformed into each other by rotation or reflection.

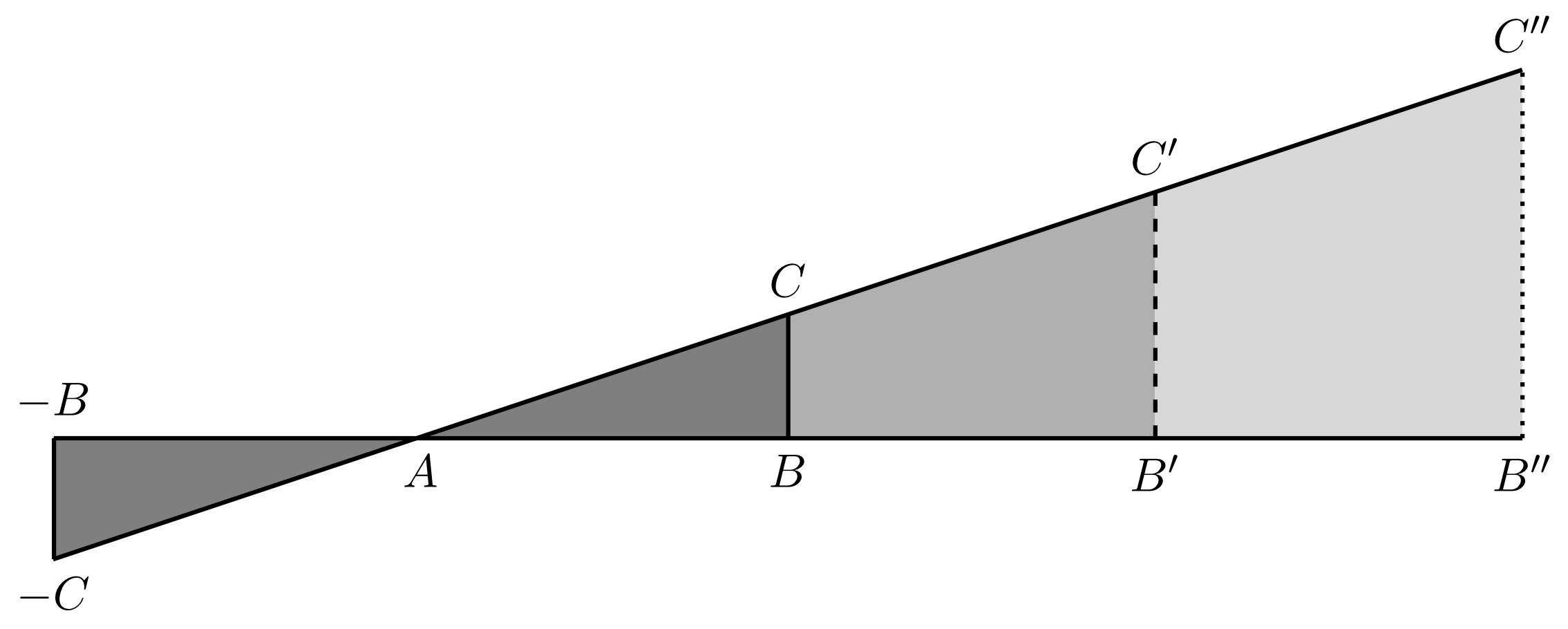
However, the triangles look similar in a way. Such similar triangles are also obtained if, for example, all the side ratios are known. This fact results from the intercept theorems as illustrated by the figure below.

Similarity Theorems for Triangles 5.3.17

Two triangles are called similar to each other if they
  • have two (and because of the triangle postulate also three) congruent angles, or
  • have three sides whose lengths have the same ratio, or
  • have one congruent angle and two adjacent sides whose lengths have the same ratio, or
  • have two sides whose lengths have the same ratio and the angles opposite to the greater side are congruent.

The right and the left triangle in Example 5.3.16 have a special relationship. The left triangle is transformed into the other by uniform scaling with the centre of enlargement S and the scaling factor k.


: